中心力场中电偶极自发跃迁的研究①
2018-12-27,,,
, , ,
(佳木斯大学理学院,黑龙江 佳木斯 154007)
1 引 言
中心力场是一种保守力场,它的势能V(r)与坐标的取向无关,具有空间转动不变性,其轨道角动量是守恒量。在过去的几十年里,中心力场的相关量子力学问题被广泛的研究。电偶极子模型也是非常重要的物理模型,其在电解质极化、电磁波的发射和吸收、生物体所有的活动与电场的作用等都可以通过建立电偶极子模型来处理。就是利用量子力学中的相关理论来研究中心力场中的电偶极辐射问题。
2 电偶极自发跃迁选择定则

(1)
其中n、n′各代表4个量子数,ω=(Enl-En′l′),上式中
(2)
三个矩阵元中至少要有一个不等于零,跃迁才是允许的。ψnljmj可以表示成
ψnljmj=Rnl(r)φljmj(θ,φ,sz)
(3)

(4a)
(4b)
(4c)
(4d)
(5)
其中径向积分与选择定则无关。利用公式
(6)
及公式
(7)
即得
(8)
类似地,可得
(9)
(10a)
(10b)
(10c)
以及Ylm的正交归一性和式(4),就可算出这些矩阵元。这样计算较之直接利用Ylm的递推公式要方便得多,特别是有利于确定选择定则。但是定性地利用Ylm的递推公式还是有益的,它们是
(11)
(12)
由此可见,量子数l的选择定则是Δl=±1,下面分类讨论。
第一种情况:
Enl→En′l′,l′→l+1,Δl=l′-l=1。
(1)φA→φA型
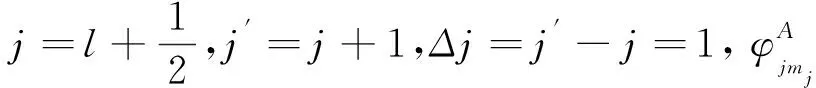
(13)
(2)φB→φB型

(3)φA→φB型

(4)φB→φA型

总结以上结果,跃迁Enl→En′l+1的选择定则为
Δj=1,0;Δmj=0,±1
(14)

第二种情况:
Enl→En′l′,l′→l-1,Δl=-1,计算类似于上一情况,选择定则为
Δj=-1,0;Δmj=0,±1
(15)
Δj=-1相当于φA→φA型或φB→φB型。Δj=0相当于φB→φA型。
第三种情况:

3 S态到P态电偶极自发跃迁的分支比
不考虑自旋时,原子中的电子状态可以表示为ψnlm=Rnl(r)Ylm(θ,φ)。对于初态为s态(能级Enl,l=0)终态为p态(能级En′l′,l′=1)的电偶极自发跃迁,初态波函数为
(16)
终态波函数为
ψn′1m=Rn′1(r)Y1m(θ,φ)
(17)
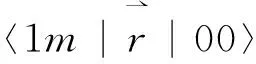
(18)
利用Ylm的正交归一性,容易求出
(19a)
(19b)
(19c)
由此可见,终态磁量子数m=1,0,-1的分支比为1∶1∶1,即由s态跃迁到三种p态的概率相等。
4 初终态l′相同和m′不同的各个终态的分支比

(20a)
(20b)
(21)
利用Ylm的递推公式
nzYlm=cosθYlm(θ,φ)
(22a)
(nx±iny)Ylm=sinθe±iφYlm(θ,φ)
(22b)

〈l±1,m|nz|lm〉
(23a)
〈l±1,m+1|(nx+iny)|lm〉
(23b)
〈l±1,m-1|(nx-iny)|lm〉
(23c)
所以跃迁到终态m′=m+1,m,m-1的分支比为
(l+m+2)(l+m+1)∶2(l+m+1)(l-m+1)∶
(l-m+2)(l-m+1)
(24)
例如初态l=m=0,终态l′=1,则m′=1,0,-1的分支比为2∶2∶2。
同理,跃迁到终态m′=m+1,m,m-1的分支比为
(l-m)(l-m-1):2(l+m)(l-m):(l+m)(l+m-1)
(25)
注意这个分支比和初态磁量子数m无关。跃迁到l′=l+1或l′=l-1态的概率(对m′求和)也与初态磁量子数m无关。
5 结 论
利用中心力场和电偶极跃迁的概念及相关知识,解决了电偶极自发跃迁的选择定则、S态到P态电偶极自发跃迁的分支比以及在初终态l,m相同或不同时,各个终态的分支比,得到了分支比和初态磁量子数m无关的结论。
