基于C语言模拟计算的粒子扰动机制分析①

(北京旌准医疗科技有限公司，北京 100176)

0 引 言

C语言于1972年诞生于美国贝尔实验室，是当下普遍使用的一种高级程序设计语言，它既包含了相关高级语言的特点，也包含了汇编语言的相应特点。C语言以其功能丰富、使用灵活方便、应用面广泛、可移植性好、易于调试和维护等优点，不仅在计算机应用领域得到了迅速推广和使用，在各类科研领域也发挥着非常重要的作用。它不仅可以用于模块化程序设计、系统软件编写、单片机系统开发等，同时具有非常强大的科研分析和数据处理能力。

目标粒子受干扰粒子的影响，其分布一般与不含干扰粒子下的分布不同。当干扰粒子对目标粒子产生的干扰作用定向性越强，目标粒子分布相对无干扰粒子下的分布，其偏离程度越大；当干扰粒子产生的干扰作用随机性越强，目标粒子分布相对无干扰粒子下的分布，其偏离程度越小，但当干扰作用完全随机时，偏离程度并非为零，而是存在一定的扰动影响。针对上述分析，利用C语言程序模拟干扰作用完全随机的情况下目标粒子进入孔洞的过程，对干扰粒子对目标粒子分布的影响进行分析与计算，从而得到干扰作用完全随机的情况下干扰粒子对目标粒子的扰动机制，这对芯片数字PCR中目的核酸进入反应通孔的芯片反应通孔数设计、流式细胞法中荧光标记粒子(可看做目标粒子)的频率分布特征分析等具有一定的应用价值。

1 模拟算法

通过C语言模拟“干扰作用完全随机的情况下目标粒子进入孔洞的过程”的模拟算法如图1所示，具体过程如下：

第一步：在[0，h+n*h/m)区间内生成m+n个随机数，其中[0，h-1]区间内的随机数代表目标粒子，总数为m；[h，h+n*h/m)区间内的随机数代表干扰粒子，总数为n；h代表孔洞数。

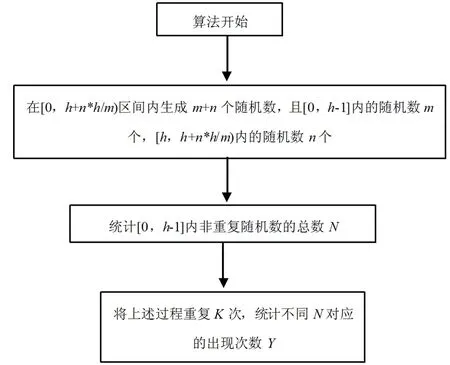
图1 模拟算法程序图

在这一步中随机数生成的关键性程序如下：

rand_ret = (rand()*(RAND_MAX+1) +

rand())%(m+n)

第二步：统计[0，h-1]内非重复随机数的总数N，N表示m个目标粒子在h个孔洞中的入孔总数；

这一步中统计总数N的关键性程序如下：

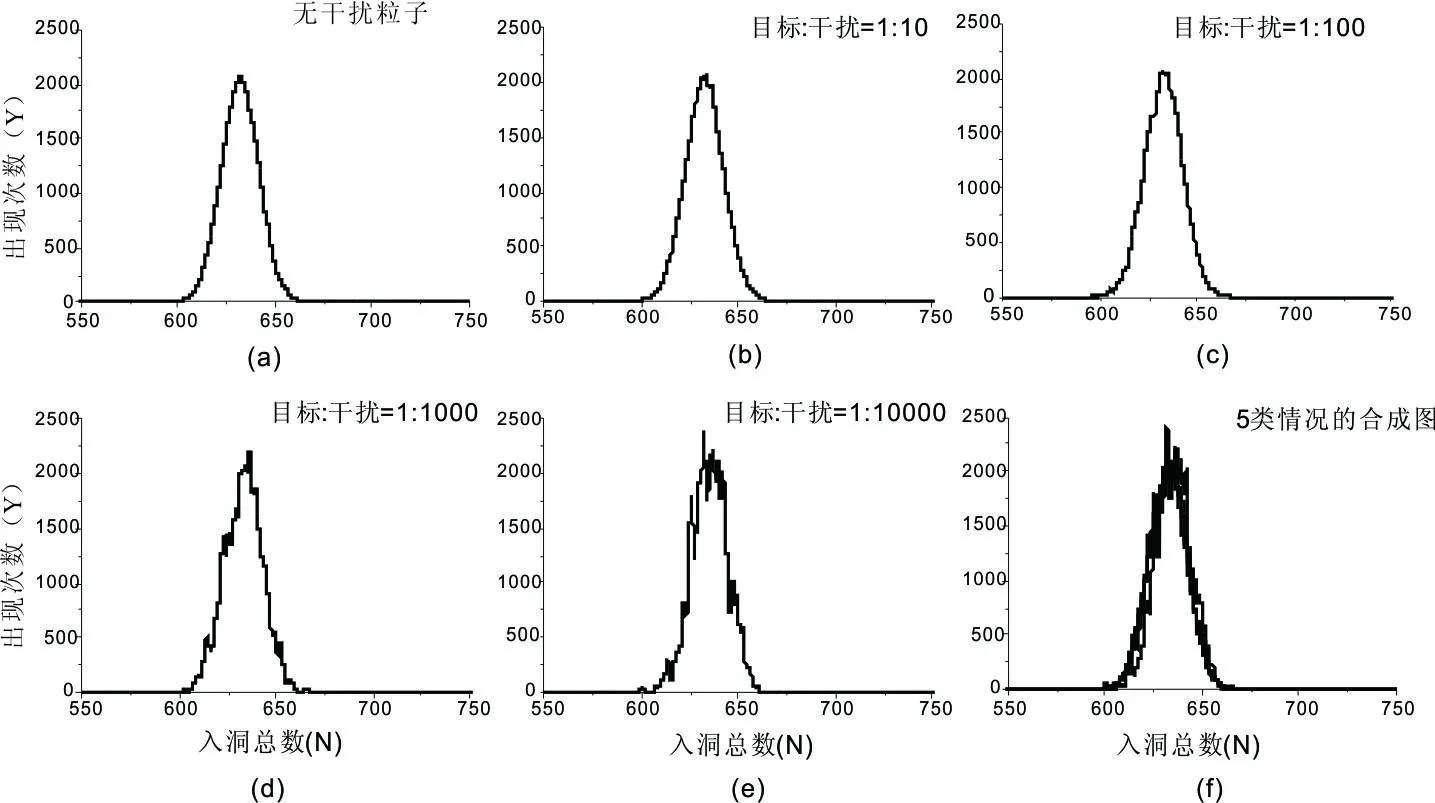
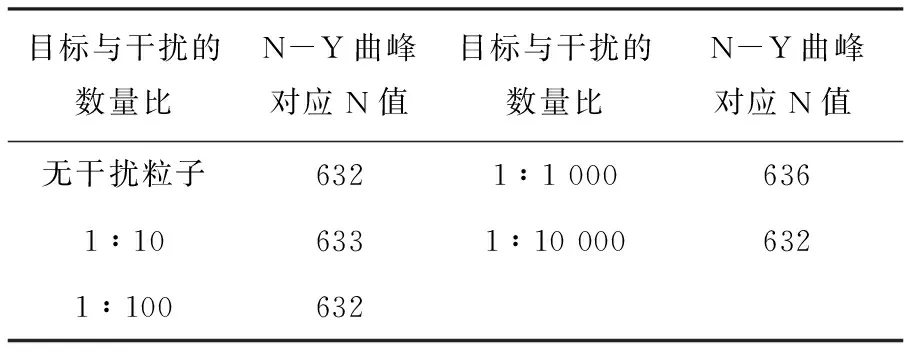
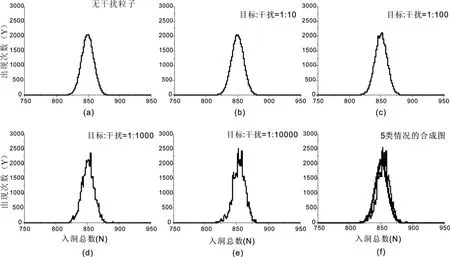
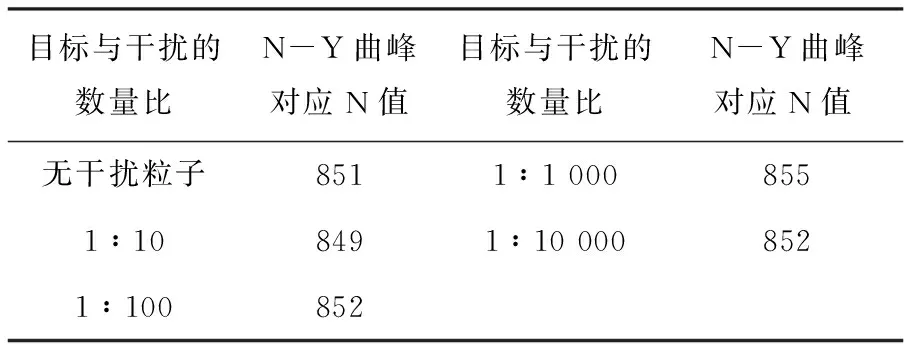
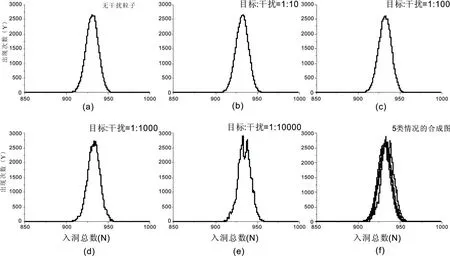
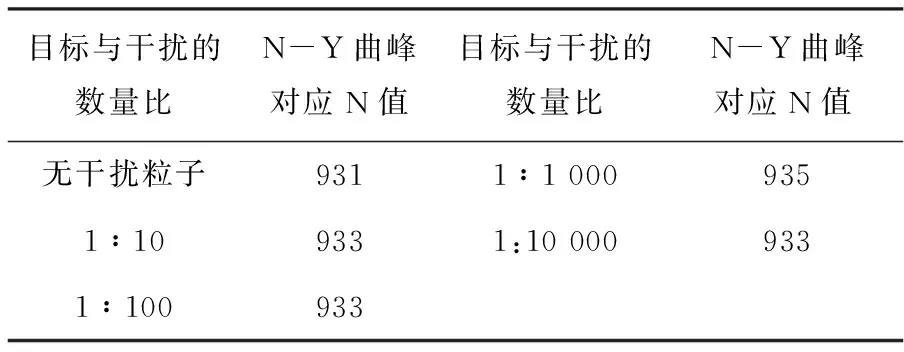
if(rand_ret

{

if(buf[rand_ret]==0 )

{

buf[rand_ret] = 1;

++sum; }

}

第三步：将上述过程重复K次，并统计不同N对应的出现次数Y；

1

2 扰动机制分析

为了分析干扰作用完全随机的情况下，干扰粒子有无及其多少对目标粒子分布的影响，根据图1所示采用如下统计分析过程：

设目标粒子个数为1 000，干扰粒子个数为1 000b(b分别取0、10、100、1 000、10 000)，孔洞数为1 000a(a分别取1、3、7)。当孔洞数取1 000时，利用C算法程序随机生成1 000+1 000b个介于[0，999+1 000b〗的随机数，且[0，999]之间的随机数1 000个，代表目标粒子；[1 000，999+1 000b]之间的随机数1 000b个，代表干扰粒子。当生成随机数x(0≤x≤999)时表示目标粒子落入标号为x的孔洞内，统计代表目标粒子的1 000个随机数的非重复数值的总数N，N就表示1 000个目标粒子在1 000b个干扰粒子作用下在1 000个孔洞中的入洞总数。将上述过程重复5万次，统计不同入洞总数N对应的出现次数Y，从而得到1 000个目标粒子在1 000b个干扰粒子作用下在1 000个孔洞中的分布情况，如图2和表1所示。

图2 目标粒子在1 000个孔洞中的分布

目标与干扰的数量比N-Y曲峰对应N值目标与干扰的数量比N-Y曲峰对应N值无干扰粒子6321∶1 0006361∶106331∶10 0006321∶100632

当孔洞数h取3000时，利用C算法程序随机生成1 000+1 000b(b分别取0、10、100、1 000、10 000)个介于[0，2 999+3 000b]的随机数，当生成随机数x(0≤x≤2999)时表示目标粒子落入标号为x的孔洞内，并统计代表目标粒子的1 000个随机数的非重复数值的总数N。将上述过程重复5万次，统计不同入洞总数N对应的出现次数Y，从而得到1 000个目标粒子在1 000b个干扰粒子作用下在3 000个孔洞中的分布情况，如图3和表2所示。

图3 目标粒子在3 000个孔洞中的分布

(a)无干扰粒子对应的目标粒子分布；(b)、(c)、(d)、(e)分别对应干扰粒子个数是目标粒子的10、100、1 000、10 000倍时的目标粒子分布； (f)前述5类情况的合成图.

表2N-Y曲线波峰对应的入洞总数N(3 000个孔洞)

目标与干扰的数量比N-Y曲峰对应N值目标与干扰的数量比N-Y曲峰对应N值无干扰粒子8511∶1 0008551∶108491∶10 0008521∶100852

依此类推，可得到当孔洞数h取7 000时1 000个目标粒子在1 000b个(b分别取0、10、100、1 000、10 000)干扰粒子作用下在7 000个孔洞中的分布情况，如图4和表3所示。

图4 目标粒子在7 000个孔洞中的分布

(a)无干扰粒子对应的目标粒子分布；(b)、(c)、(d)、(e)分别对应干扰粒子个数是目标粒子的10、100、1 000、10 000倍时的目标粒子分布； (f)前述5类情况的合成图.

表3N-Y曲线波峰对应的入洞总数N(7 000个孔洞)

目标与干扰的数量比N-Y曲峰对应N值目标与干扰的数量比N-Y曲峰对应N值无干扰粒子9311∶1 0009351∶109331:10 0009331∶100933

从图2到图4发现，不论孔洞数h为多少，含干扰粒子的4类N-Y曲线分布与不含干扰粒子的N-Y曲线分布基本重合或相同，且干扰粒子个数越小，其对应的N-Y曲线分布与不含干扰粒子的N-Y曲线分布的重合度或相似度越高；而从表1到表3同样发现，不论孔洞数h为多少，含干扰粒子的4类N-Y曲线的主峰对应的N值与不含干扰粒子的N-Y曲线的主峰对应的N值几乎相同。上述结果表明，在干扰作用完全随机的情况下，对于任意取值的孔洞数h，干扰粒子有无及其多少不会破坏目标粒子的随机分布程度，这决定了无论有无干扰粒子或其存在多少，目标粒子都将具有基本相同的N-Y曲线分布。

但是，从图2到图4可以发现，当加入干扰粒子时会引起目标粒子N-Y分布曲线的局域统计波动或涨落(即N-Y曲线中的锯齿波动)，且随着干扰粒子个数逐渐增多，目标粒子N-Y分布曲线的局域统计波动或涨落也越大。这样的结果表明，加入干扰粒子后目标粒子的入洞总数N将发生局域统计波动或涨落，且随着干扰粒子个数的增多，入洞总数N的局域统计波动或涨落越大，但这种局域统计波动或涨落不会影响目标粒子的整体N-Y曲线分布。

3 结 论

利用C语言模拟干扰作用完全随机的情况下目标粒子进入孔洞的过程，对干扰粒子对目标粒子分布的影响进行了分析与计算，得到了如下结论：

在干扰作用完全随机的情况下，对于任意取值的孔洞数，干扰粒子有无或其多少均不会破坏目标粒子的随机分布程度，因此，无论有无干扰粒子或其存在多少，目标粒子都将具有基本相同的N-Y曲线分布，但是干扰粒子会引起目标粒子入洞总数N的局域统计波动或涨落，且随着干扰粒子个数的增多，局域统计波动或涨落越大，但这种局域统计波动或涨落不会影响目标粒子的整体N-Y曲线分布。

上述结果不仅可以应用于芯片数字PCR的芯片反应通孔数设计、流式细胞法中荧光标记粒子的频率分布特征分析等设计与分析过程，对于众多涉及需要在干扰背景下对目标粒子的分布与状态进行处理分析的过程，由于定然需要对目标与干扰粒子之间的扰动机制问题进行分析与解决，因而上述结果在实际生产和生活中对于其它众多干扰环境下目标粒子的处理问题同样具有一定的普遍应用价值。