汽车减振器性能检测伺服模糊PID控制研究①

, , ，

(1.皖西学院机械与车辆工程学院,安徽 六安 237012； 2 合肥工业大学机械工程学院,安徽 合肥 230009)

0 引 言

汽车振动的衰减通过轮胎、悬架、座椅三个环节实现，其中起主要作用的是悬架系统。悬架性能差的话，在汽车高速行驶的过程中就会出现剧烈颠簸而不得不降低汽车的行驶速度。通常情况下，减振器的实际工况较复杂，在实际设计减振器的过程中，需要使用试验台对减振器进行性能试验，通过比较试验结果和理论计算结果调整减振器设计过程中的参数，减小理论与实际的性能误差，利用传递函数法分析和模糊PID控制进行电液伺服系统的动态特性分析。

1 控制原理

1.1 电液比例伺服原理

如图1所示电液比例伺服控制原理图[1,2]。电液伺服控制的主要控制部分就是电液伺服阀，采用合适的控制器对液压缸位置信息进行模拟量和数字量之间的转换与处理，根据液压缸位置反馈给控制器，通过模糊PID控制器或其它类型的控制器实现对电液伺服阀的控制。

对电液伺服阀控制时要测得伺服阀的传递函数模型，伺服阀的传递函数可表示为：

(1)

式中G为传递函数；s为传递函数变量；K为电液伺服阀流量增益；ω为电液伺服阀固有频率；ζ为电液伺服阀阻尼比。

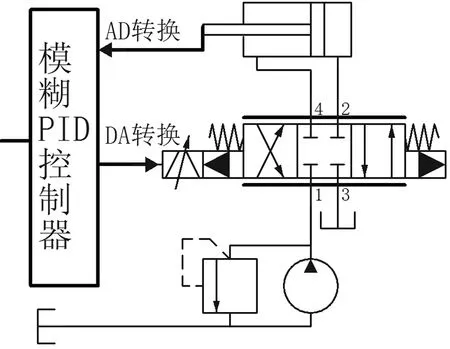
图1 电液伺服驱动原理

1.2 PID控制

PID控制策略算法简单，可靠性高，鲁棒性好，已被广泛应用于过程控制和运动控制中[3,4]。数字PID控制是生产过程中普遍采用的控制方法，将偏差的比例、积分、微分通过线性组合对被控对象进行控制，离散PID控制模型为[5,6]：

(2)

式中u为PID控制器的输出；k为离散点；kp为比例常数；ki为积分常数；kd为微分常数；e(k)为当前偏差；e(k-1)为上一次偏差。

实际生产过程往往具有非线性、非定长等特点，难以建立精确的控制模型，所以应用常规的PID控制很难达到较好的控制效果[7,8]，实际控制过程应采用智能PID控制以得到较好的控制效果和性能，满足对工况的适应。

1.3 模糊规则与模糊集

模糊控制器是模糊控制系统的核心，模糊控制器的结构，采用的模糊规则等因素影响着模糊控制器的优劣。模糊控制器组成框图如图2所示。图2中知识库包括两个部分：数据库和规则库。数据库存放的是模糊子集的隶属度矢量值，向推理机提供数据，规则库是按人的直觉推理的语言表示形式。

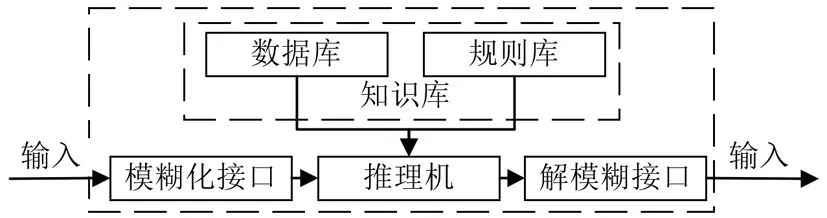
图2 模糊控制器组成

图3 模糊PID控制程序仿真流程

仿真实验对模糊控制器的输入采用[负大，负中，负小，零，正小，正中，正大]，即[NB，NM，NS，Z，PS，PM，PB]模糊子集[9,10]，确定模糊控制器的输入变量结构如表1所示。

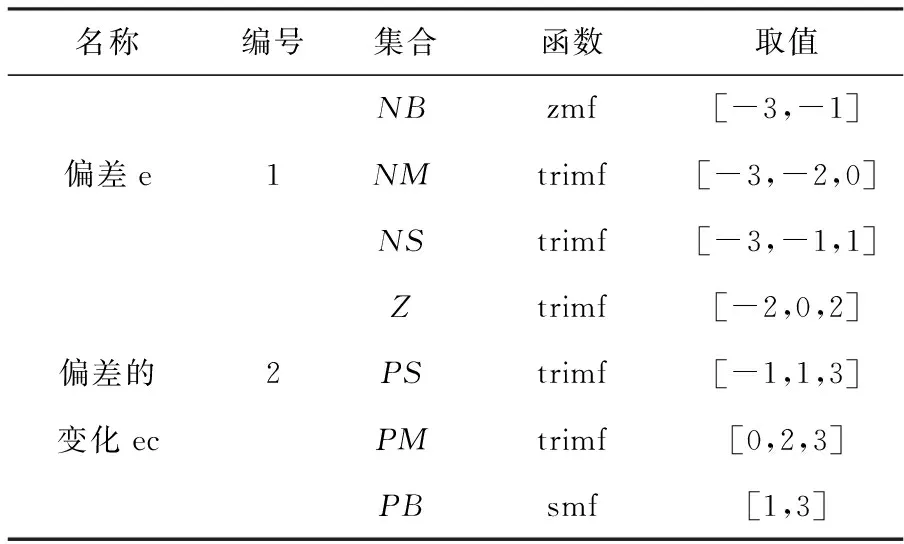
表1 模糊推理输入变量隶属配置

同理可配置输出变量的语言变量为：

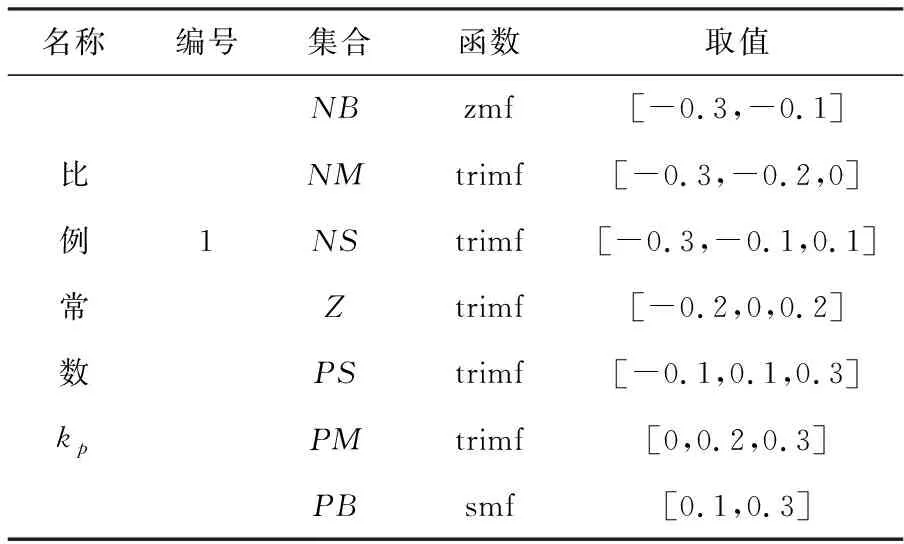
表2 比例常数隶属配置

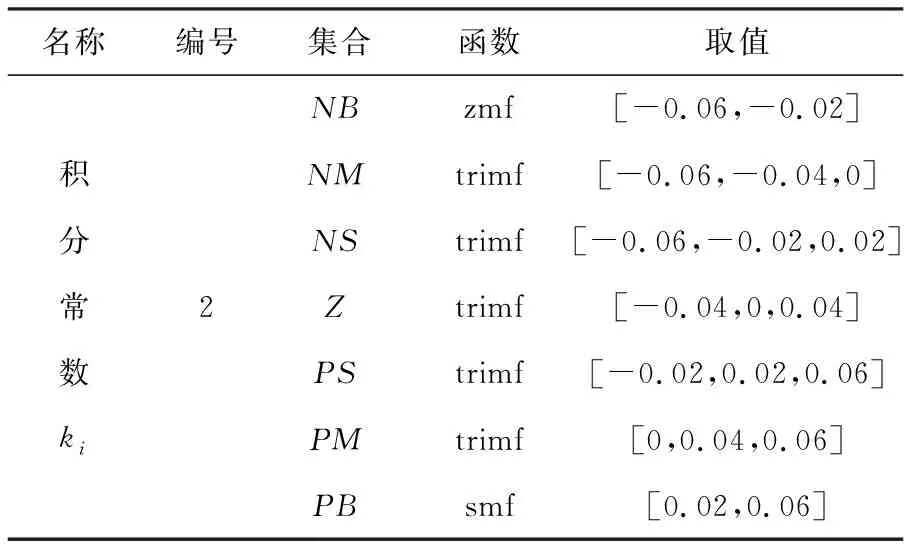
表3 积分常数隶属配置

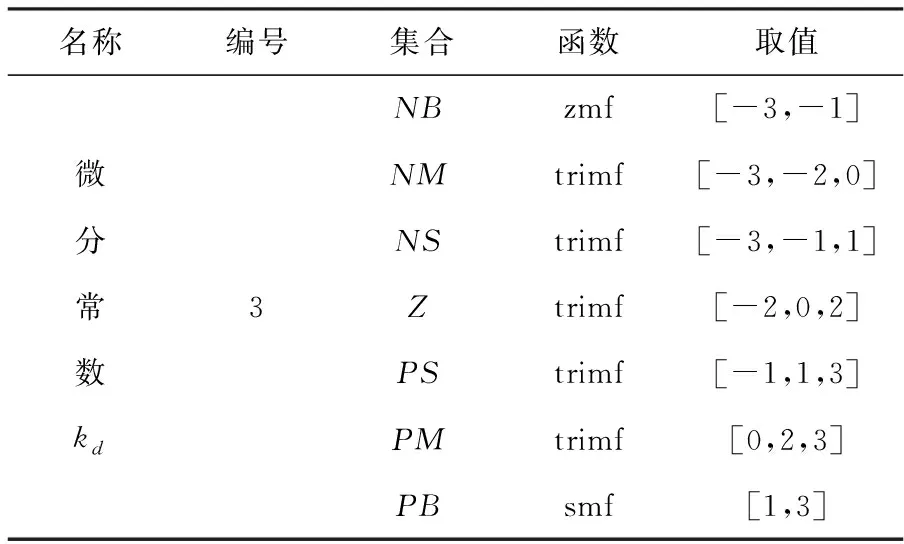
表4 微分常数隶属配置

1.4 模糊整定PID参数

经过模糊推理后得到PID参数的整定数值，建立模糊PID整定模型：

(3)

式中kp、ki、kd分别为经过模糊推理整定后的比例、积分、微分常数；kpr、kir、kdr分别为初始给定的比例、积分、微分常数；fp、fi、fd分别为模糊推理得出的比例、积分、微分常数；α、β、η分别为模糊推理的比例、积分、微分增益。

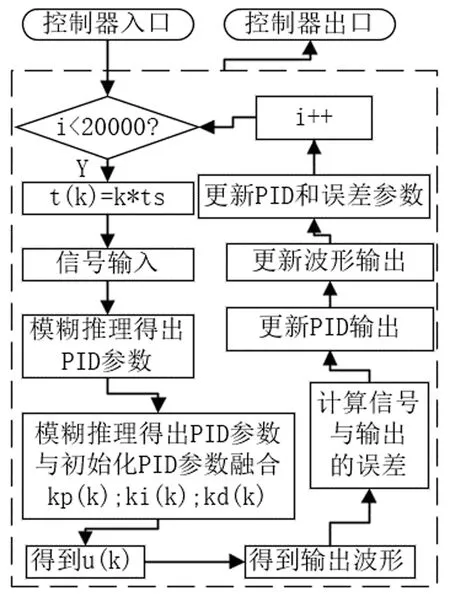
图4 模糊PID控制器流程

2 模糊PID控制MATLAB编程

2.1 程序流程

根据模糊控制规则与PID控制模型，应用MATLAB进行模糊PID控制的编程与仿真。MATLAB编程流程如图3所示。

创建模糊参考系统和向推理系统添加输入输出变量根据表1、表2和表3进行配置。模糊规则配置为7个元素变量(2个输入变量，3个输出变量和2个权重及条件关系)，配置权重为1，条件关系为AND型。设置反模糊化方法为最大隶属度平均法即DefuzzMethod=mom。配置PID的采样周期为1ms，进行20s的仿真计算。

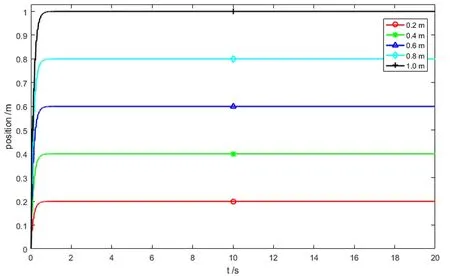
图5 电液伺服模糊PID阶跃位置控制

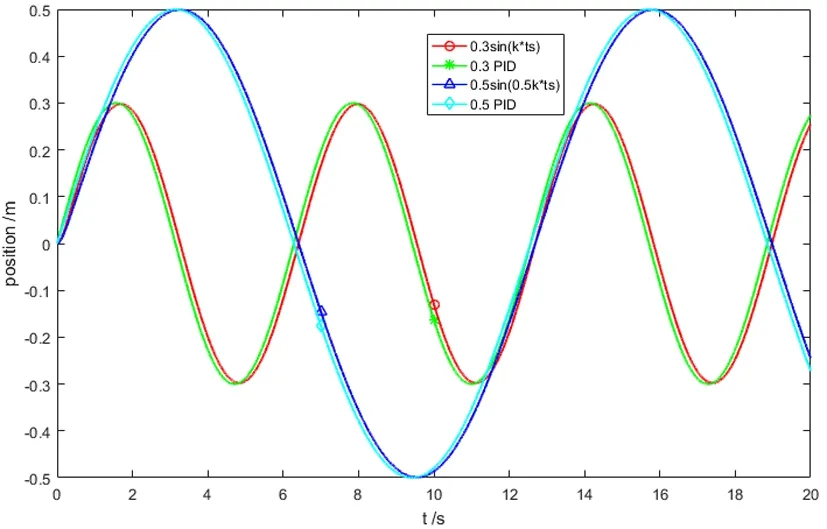
图6 电液伺服模糊PID简谐激励控制

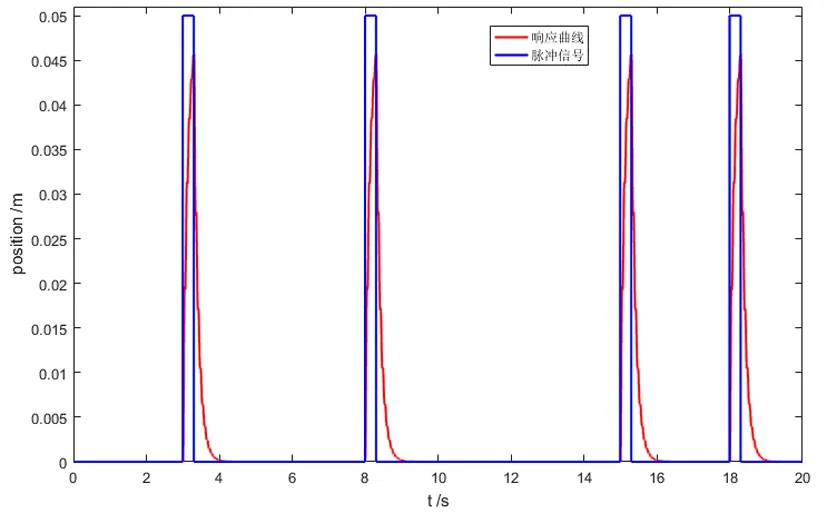
图7 电液伺服模糊PID拟脉冲响应

2.2 模糊PID控制器设计

加入模糊控制以后，常规的PID控制要进行相应的变化，具体程序流程如图5所示。程序进行20000次循环迭代，得到总运行时间为20s的输出波形，通过对比输入信号波形和输出波形可得到控制器的稳定性及优劣性质。

图4中t(k)为离散数据运行的离散时间值，ts为采样周期，方便后序数据处理使用，通过模糊推理器得到经过模糊推理后的PID参数值，与初始化PID参数进行加法融合，就得到了能够运用于系统的PID参数值，从而可得模糊PID整定后的u(k)值，根据传递函数关系，便可得到想要输出的波形。随后要进行输入信号与控制器输出值的误差，以及更新PID输出、波形输出和PID及误差参数，为下一次迭代提供新的初始值。

2.3 控制器仿真分析

根据设定好的模糊PID控制器进行输入为0.2 m，0.4 m，0.6 m，0.8 m和1.0 m的阶跃响应仿真，同时为了分析系统的精确性，进行两次简谐波激励仿真，简谐波方程设置为0.3sin(kts)和0.5*sin(0.5kts)。根据检测装置的工况特性，进行脉冲高度为0.05 m的拟脉冲响应仿真，结果如下。

由图5可知，模糊PID控制克服了一般PID控制超调的缺陷，系统进入稳态的时间较短且振动较小，达到了较理想的控制效果。

由图6可知，模糊PID位置追踪效果较好，与输入信号波形几乎完全重合，所以系统能够根据信号的不同产生不同的激励响应，且响应快速精确，综上仿真分析结果可得系统的模糊PID控制能够达到较理性的控制效果。

根据图7可知系统能够根据脉冲信号的输入发生响应的变化，脉冲响应速度较快，响应曲线的稳定性也较好，没有出现较大的震荡，故该系统能够对脉冲信号有较好的控制输出。

3 结 论

基于模糊PID控制理论，设计实现了一种电液伺服控制器模型，运用MATLAB实现了控制器的编程与仿真。对系统进行的阶跃响应仿真和简谐激励响应仿真结果表明该系统工作稳定，响应速度快，超调量小，达到了较理想的控制效果。