基于柏林噪声的心脏纹理图细化①

2018-12-27,,

佳木斯大学学报（自然科学版） 2018年6期

关键词：插值振幅柏林

, ,

(福州大学物理与信息工程学院，福建福州 350116)

0 引言

构建复杂的表面，经常需要在纹理中加入一些可控的随机变化。比如不同的木板纹路，大理石纹路以及水面等等。

这就需要引入可控的随机特征——噪声。总的来说，图形学中的噪声表示为连续的变化函数，而且没有明显的重复特征。

大多数的噪声函数都在R2上的整数格子的建立，比如对于(1.2,1.3,2.4)(1.2,1.3,2.4)点，则对由(1,1,2)(1,1,2)和(2,2,3)(2,2,3)构成立方体的八个整数顶点进行操作。然后得到各个顶点的数据后进行插值操作，计算特定点的噪声值。

噪声的随机产生需要随机数，而且必须满足相同的输入产生相同的输出。如果要高效地产生和坐标相关联的随机值，通用的伪随机数产生器并不适用，常用的方法是使用哈希函数常表查找参数。Perlin噪声函数是最常用的噪声函数，称为Perlin噪声。Perlin噪声在全部(x,y,z)(x,y,z)整形顶点处的参数值都为0，变化源自各顶点间的梯度向量，然后再进行平滑插值。

1 柏林噪声函数

1)一般情况下，可将噪声函数理解为种子随机发生器。一个噪声函数需将一个整数当做参数，进而基于此参数返回一个随机数。若两次传回的参数相等，此函数即可产生两次一样的数。图1所示为一噪声函数案例。横坐标上个点均代表一个随机数，范围为0至1。

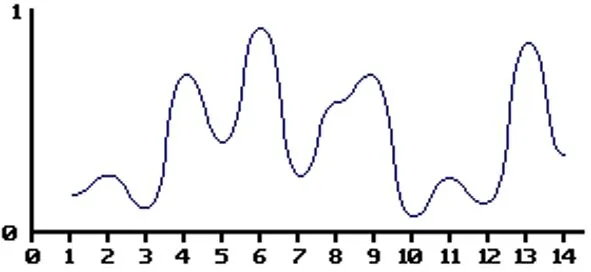
图1 噪声函数

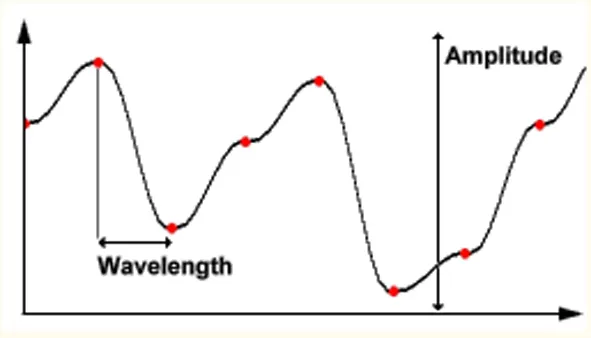
图2 噪声函数波长及幅度

图2所示红点代表函数所定义的各随机值。在此类状况下，振幅为此函数最大值同最小值之差。波长为两随机值间的水平距离。频率则等于1/波长[1]。

若使用若干平滑函数，则会具备不同的频率与振幅，可叠加这些平滑函数，由此所创建得躁声函数即为柏林噪声函数。将下述2维噪声函数进行叠加，可得到如3图所示的柏林噪声函数。

图3

叠加上述函数后所得的噪声样式：

图4

2)在叠加噪声函数过程中，每次叠加会应用到相应的振幅与频率。通常需要掌握这些振幅与品频率信息。如以上所提及的一维案例，在每个连续叠加时所应用到的频率与振幅分别为2倍、1/2倍。此案例非常常见，从而易忽略其它频率与振幅的应用。严谨起见，应借助每步应用其它频率与振幅的操作来完成特征各异的柏林噪声函数的创建。例如，在对平滑滚动的丘陵进行创建时，可应用低频率与高振幅这一特征表现的柏林噪声函数，此外，低振幅与高频率可完成平地的创建；低频率与低振幅可完成颠簸度很高的平面的创建。

3)通过持续度(Persistence)一词的应用能够简化上述过程，更易于理解，且可不再重复提及频率与振幅[2]。持续度指的是每个频率下的振幅。持续度与其客观内涵存在一定的歧异。此概念的提出者为Mandelbrot，该提出者同时在分形现象的发现中发挥作用。其界定噪声具备数量客观的高频率所呈现的持续度会较低。“持续度”的提出者还包括Matt[3]，然而其定义此概念的方式有所不同。对于上述两种定义方式，笔者更倾向于后一种，即:

frequency=2i

amplitude=persistencei

在上式中，i代表被叠加的第i个噪声函数。通过以下图表能够获知柏林函数在输出上Persistence状况。图4表对叠加的各个构成单元加以呈现，还呈现出持续度效果以及柏林函数最终结果[4]。

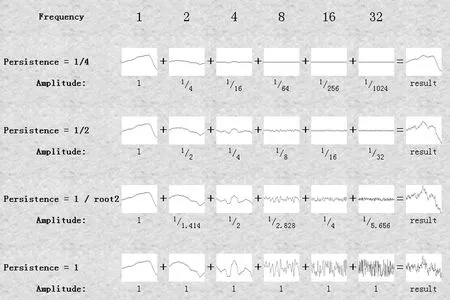
图5 噪声叠加状况表

2 插值

1)在完成目标噪声函数创建后，需对此噪声函数的返回值进行平滑处理。再次，可选择的方式众多，然而在效果上存在区别，有些具备良好效果。典型插值函数涉及3个输入：a、b以及x。应于a与b间实施插值，x的取值区间为0至1。X取值决定了插值函数具体返回至何值。若x为0,其返回a,若为1，则返回b。若x取值大于0且小于1，其会返回a至b间的某值。

应用线性插值[5]途径能够确保插值函数于插值点上的输出结果无误，然而无法确保插值点上插值函数所对应的导数。

就所生成曲线的平滑程度而言，相比线性插值，余弦插值更佳。但后者存在速度稍慢这一不足。

除了可保证函数输出外，Hermit插值[6]途径还可确保插值点上插值函数的导数等于0，如此可满足平滑性要求。

若再将插值点位置插值函数的二阶导数取值设定成0，那么能够实现平滑度的进一步提升。5次插值函数如下：

s(x) = 6x5-15x4+10x3

图6差值过程

图5所示各小块均为不同的采样率应用下杂点纹理随机采样结果。所展示的细节随着采样率的下降而变少，反之所获细节愈多。左上角小块应用的最低采样率，所得细节最少。右下角小块则应用了最高采样率，所得细节最多。通过这6张小图用来合成最终柏林噪声。当进行合成时，在合成比重上，各张小图有所区别，细节愈少，所占用的合成比重愈大，反之则愈小。以上图为例，左上角小图的采样纹理关系到最终柏林噪声的基本样式，其余5张小图的全部纹理逐一叠加构成了细节构建，然而比重逐渐下降。

所合成的柏林噪声[7]最终显示为图7:

图7 柏林噪声图

2)样图细化

纹理所指为物体表面的一种视觉体现，其可体现物体表面光泽、质地与颜色等信息，由此来同其它物体加以区分。在计算机中可视为一类二维平面，凭借一定映射途径映射至三维物体表面上。针对样本，此次研究选用纹理合成途径[8]。首先应保证所选择的数据源具备非均匀各向异性、高精度，故而，将数据源确定为心脏切片图，详见图8。

经过柏林噪声处理后的纹理细化图9：

3)心脏体的构建

图8 心脏切片纹理图

图9 心脏切片纹理细化图

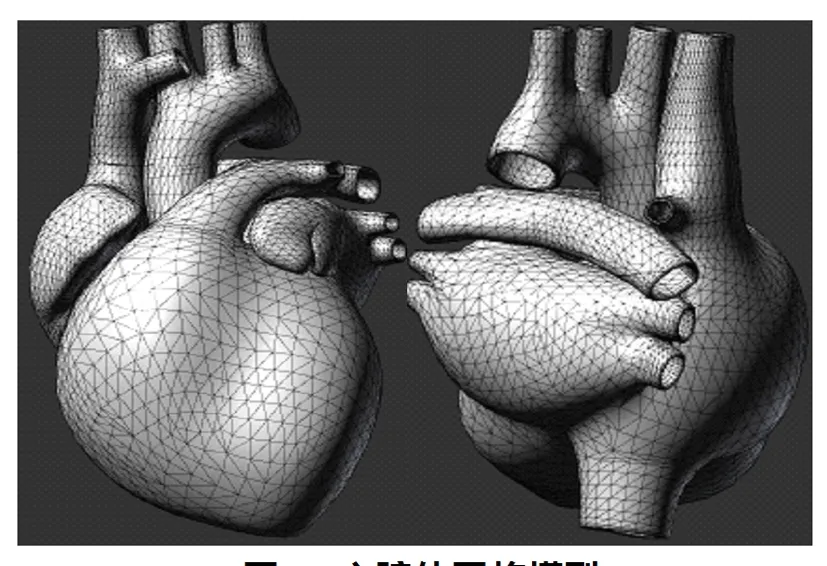
图10 心脏体网格模型

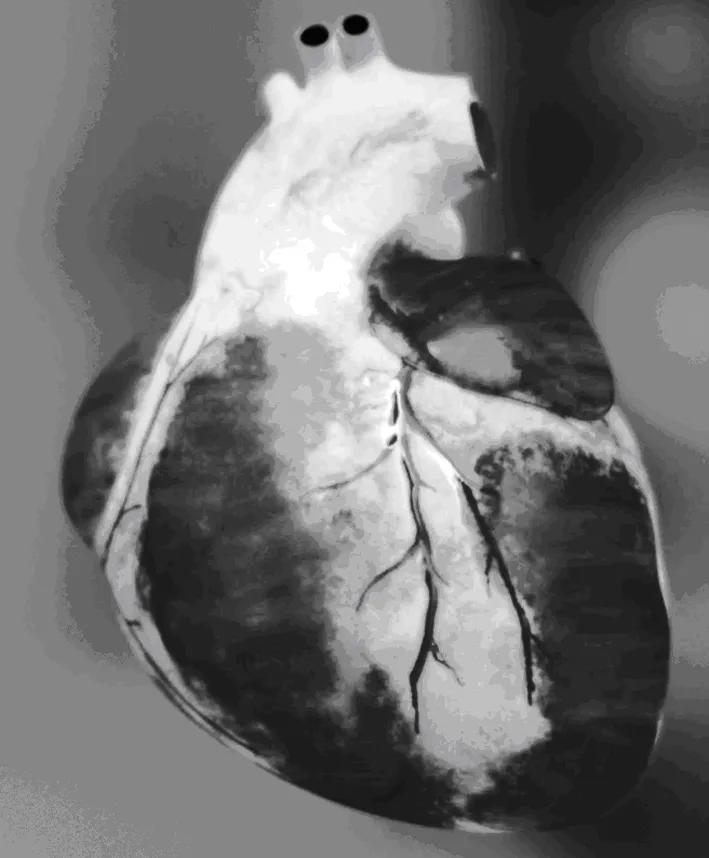
图11 心脏合成效果图

为了确保所构建的心脏模型满足精度要求，第一步通过Maya软件完成心脏体原型的构建；第二步，在软件内完成以obj为后缀的模型文件的导出操作，此模型结构呈网格状(详见图1)。由于仅通过表面网格构造不能充分展示心脏内部，故而，应借助模型转换工具(3D Object Conveter)[9]把完成构建的心脏模型生成为以ply为后缀的文件，然后借助四面体网格生成库转换心脏网格为三角体网格，如此可利于纹理贴图。保存三角体网格模型为ele文件、node文件。其中，前者内含此模型各顶点所链接的索引信息；后者内含所有顶点的位置信息。此次研究所构建的心脏三角网格体模型所含三角网格与顶点分别为17718个、10007个，如图10。