基于改进光流法的血流仿真方法研究①

，

(福州大学物理与信息工程学院，福建 福州 350116)

0 引 言

在手术中，流血现象十分的常见，血流仿真的真实感和实时性就显得十分必要，国内外的大量专家学者对此进行了研究。

关于流体的模拟研究，一直是虚拟手术中研究的热点和难点，从本世纪开始，流体模拟研究的新方法和新思路就开始大量涌现。2015年, 肖苗苗等人[1]使用异构计算平台Open CL对SPH(smoothed particle hydrodynamics)方法进行加速,充分利用了Open CL与图形渲染API的数据互通；2015年，Ladicky等人[2]提出一种用数据流驱动的方法来模拟流体的流动。

血流模拟的主要难点是兼顾血流流动的真实感和实时性，上面提及的方法侧重于改善流体模拟的实时性，而忽略了流体模拟的真实感。为此，在研究中引入了基于梯度的光流法。由于一阶近似在大范围速度场中误差较大，提出一种新的迭代方法，优化速度场的细节，增强血流模拟的真实感。针对FLIP方法中网格插值粒子过程中计算误差较大的问题，对原有的插值方法进行改进，以减小误差，提高仿真的精度。

1 光流法

拟引入光流法对流体表面的速度场进行求解，并在前人研究的基础上对求解过程的相关方法进行改进，以提高求解精度。

光流法求解速度场可分为以下几步：离散求解、迭代计算和表面投影。下面对求解过程作一个简单的介绍。

1.1 离散求解

(1)

接下来引入两个常见的正则化矩阵：一个平滑矩阵，和一个支持较小速度场矢量的矩阵(也叫做Tikhonov 正则化矩阵)。要计算速度场u，需要将公式(1)的数据项和两个正则化矩阵最小化，然后最小化能量项的加权和，方便接下来计算速度场：

(2)

在最小二乘意义上的离散情况的能量最小化由下式给出

βS∑j|uj|2+βT|u|2dΩ

(3)

在式中，βS和βT分别表示对应项的比例因子，∑j表示四个维度上的和。Φr是光流应用的时间导数, 即参数r引起的变化。通过Φ2来计算空间梯度，其中，Φ2是通过计算要得到的速度场。

公式(3)的离散最小化产生如下一个线性方程组

Aofu=b

(4)

通过上式计算u。矩阵Aof包含离散化的能量项，见下式。

Aof=[Φ2]T[Φ2]+βS∑jLj+βTI

(5)

公式(5)中的三项分别对应前面提到的数据项、平滑度和Tikhonov项。[Φ2]表示一个n×4n的矩阵，这个矩阵包含Φ2的离散梯度，L表示离散的拉普拉斯矩阵。公式(4)中。

b=[-Φ2]TΦr，Φr=Φ2-Φ1

由于公式(1)中的第二项是非线性项，在实际应用中很难线性化，所以在实际应用过程中常常对对应的导数采取一阶近似的方法[3]。

1.2 迭代计算

迭代方法结合了递归重采样的分层和在粗糙层次改变数据使之发生变化这两种方法[4]，有助于减少一阶近似所产生的误差。

如果第一个通过光流法计算得到的速度场与预期理想的速度场较为接近，那么就可以除去有误差的部分，用剩余的部分产生第二个速度场u2，这个过程称之为剩余迭代，迭代进行到无法计算或者输出结果的质量不理想为止。

迭代的重新线性化使输入更符合我们的要求，它与分层相结合的解决方案能显著改善速度场的最终质量。

1.3 表面投影

计算好速度场后，需要把速度场从源表面投影到目标网格上。给定一个通过光流法产生的速度场，执行一个二分法搜索每个单元沿着目标的梯度，直到在网格上找到与源单元表面值相匹配的点。将投影作为估计当前速度场值uk的一个更新步骤，其递归公式如下。

uk+1(x)=uk(x)+bisect(x+uk(x),-

n(x+uk(x)))

(6)

公式(6)中，函数bisect表示第一个参数沿着第二个参数传递的方向进行的实际查找。在这种情况下，n是指目标Φ2的正定化梯度，且通常是体积内点的反转。

2 血流与固体的交互仿真

对血流与固体的交互过程进行仿真，首先将血液粒子化，用求得的速度场驱动血粒子运动完成血液的整体流动，

2.1 FLIP方法

血液粒子化后，引入了FLIP(Fluid Implicit Particle)[5]的方法实现网格到粒子的插值计算。FLIP方法的步骤如下。

1) 初始化血粒子位置和速度。

2) 在交错的mac网格节点上，计算附近粒子速度的加权平均值，并将速度保存。

3) 用保存的节点速度减去更新后的节点速度，对每个粒子进行插值。

4) 以网格节点速度值驱动血粒子的运动。

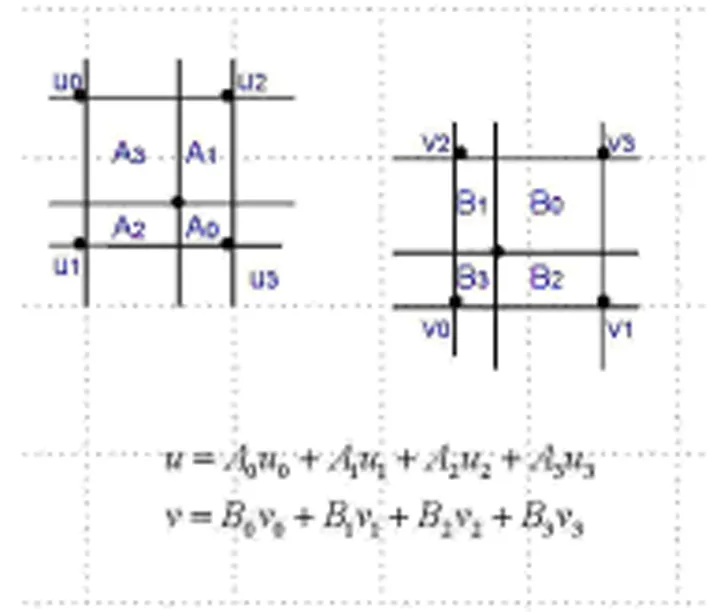
图1 网格到粒子的插值

针对第3步的插值方法，提出一种改进的平流算法[6]的方法，以减少插值计算的量。方法简要概述如下：一个单参数x1和两个带有速度场u1→2和u2→1的输入Ψ1和Ψ2。在这种情况下插值结果Ψ0由下式给出

(7)

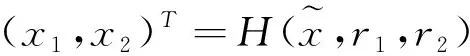
(8)

其中advect是平流算法，p为插值点，r为参数。公式(7)即为常规的重心转换。

2.2 渲 染

血流与粒子交互的过程中，需要将粒子抽取成表面并渲染。这一过程将用到Marching cube[7～8]算法，该算法的核心是抽取等值面并按一定的方式连接起来绘制一个整体的表面。

整个交互过程的流程图如下

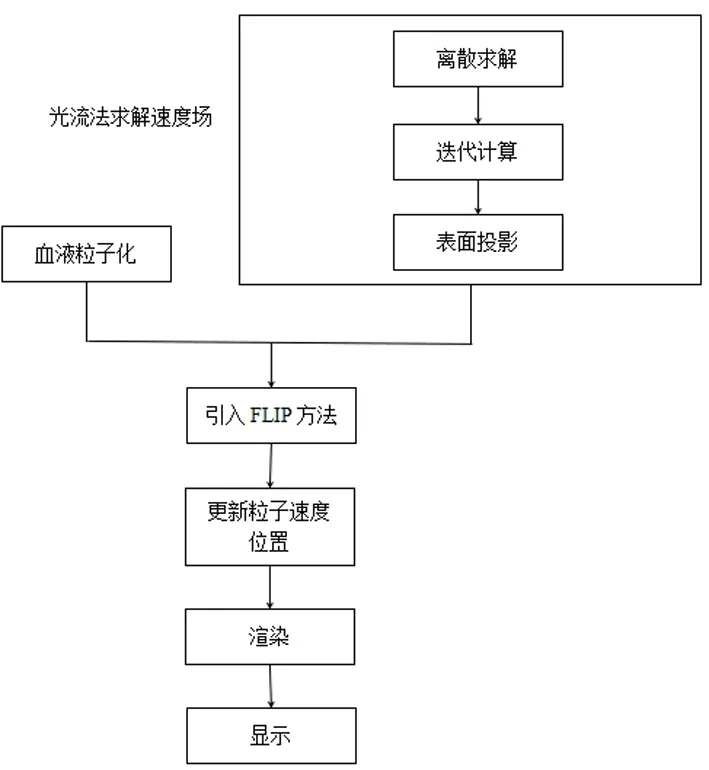
图2 血流仿真整体流程图

3 仿真过程及结果

实验环境介绍如下。硬件环境为：Intel Core i5-3210M，主频2.5GHz，4G内存，显卡为NVIDIA GEFORCE GT 635，显存2G。软件环境为：操作系统为Windows 7系统(64位)，开发环境为Microsoft Visual Studio 2013(Win 32)，算法语言为C++，生成manta可执行程序，通过打开相应的Python文件，调用OpenGL库渲染来达到仿真的效果。

下图是血流向下流动时与固体相遇交互的场景仿真，分别是第14、44、74、104和134帧的图像。

图3 血流与固体交互过程

图3所示过程可以看出，血流自上而下流动，遇到固体时，血流分成两股，分开后的血流在固体下方流动一段距离后又逐渐合成一股。下表是相关的统计数据。

表1 血流与固体交互仿真效率的分析

从表1可以看出，随着流体粒子数的增加，更新粒子所用的时间相应地变长了，但从74帧以后，更新流体粒子的时间间隔趋于稳定，整体来看，改进后的算法处理效率高。

由于血流表面的投影是在欧拉网格上进行的，因此网格数对表面的仿真精度有着重要的影响，下表显示了在不同网格数的情况下仿真动画的FPS(帧率)。这里的帧率取的是平均值。并与文献[9]中的FPS结果进行对比。

表2血流与固体交互仿真中不同网格数对应的FPS

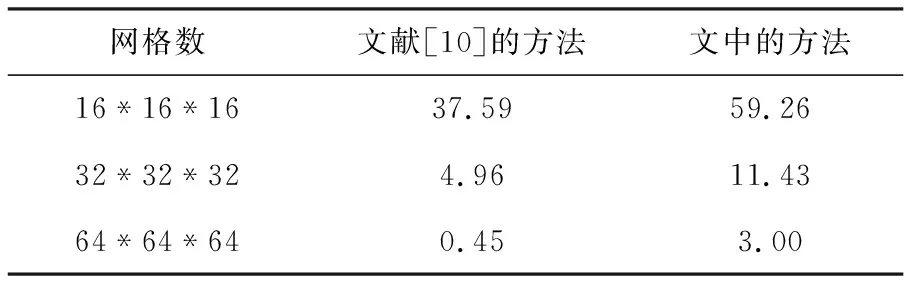
网格数文献[10]的方法文中的方法16*16*1637.5959.2632*32*324.9611.4364*64*640.453.00

随着网格数量的增加，计算量也相对增加，流体动画的帧率在下降。研究中，在粒子数等变量一定的情况下，从表2可以看出，相比文献[9]的方法，文中的方法在网格数相同的情况下，FPS都相对较高，故仿真的精度较高，血流仿真的效果较好。

4 结 语

从血流仿真的真实感的角度出发，研究中引入了基于梯度的光流法。由于一阶近似在大范围速度场中误差较大，提出一种新的迭代方法，优化速度场的细节，增强血流模拟的真实感。针对FLIP方法中网格插值粒子过程中计算误差较大的问题，对原有的插值方法进行改进，以减小误差，提高仿真的精度。实验结果表明，文中的方法基本满足血流仿真中真实感和实时性的要求。