动态自适应人工鱼群算法研究

陈桂霞

（江苏联合职业技术学院扬州分院 信息工程系，江苏 扬州 225000）

标准人工鱼群算法（Standard Artificial Fish Swarm Algorithm，AFSA）具有快速性收敛性，在运行过程中，鱼群在初期会呈现出较快的聚集现象，迅速向最优个体靠拢。但是，当人工鱼群运行到后期的时候，由于采用的步长、视野等参数缺少变化，其收敛速度会明显变慢，而且容易使算法跳过最优，导致算法的解精度降低。本文研究一个能有效提高人工鱼群算法解精度的方法—参数自适应变化机制，该方法令人工鱼群算法的两个主要参数visual和step，在一定范围内自适应动态变化[1]。

1 参数自适应机制

根据相关研究可知，参数visual决定了个体鱼的搜索范围，如果visual较大，则鱼个体的搜索范围比较广，能够发现更多的最佳个体，可保证较强的全局搜索；如果参数visual较小，则鱼个体的搜索范围较小，会局限于该个体的周围，以保证精细的局部搜索。

根据群体智能算法的空间搜索机制可知，群体智能算法在运算早期应该着重于全局搜索，以保证较快的收敛速度和广阔的搜索范围[2]。在运算后期则应该着重于精细的局部搜索，针对最佳个体周围邻域进行搜索，以提高算法的求解精度。故visual的变化采用动态机制处理要优于固定机制，考虑到logistic模型的动态变化性，故采用logistic模型对visual进行调整。设visual的变化范围是[visualmin,visualmax]，则参数visual的变化设定为公式1。

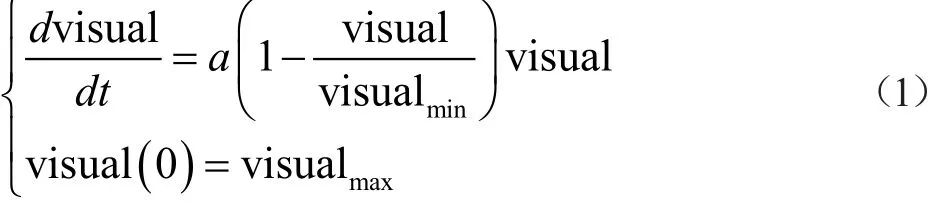
根据该模型，可得到visual的缩放变化公式2。

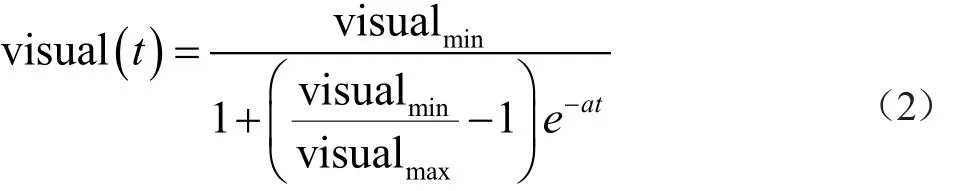
公式中，t为算法的迭代次数，a为初始衰减率，用于调整visual的下降速度。a的初始值越大，visual的下降速度越快；反之，visual的下降速度越慢。从公式1可以知道，当t=0时，visual(t)=visualmax，随着t不断迭代增加，visual逐渐收敛于visualmin。

由人工鱼群算法的计算原理可知，步长step亦会影响算法中个体的搜索范围。step越大，个体鱼向最优位置靠近的速度越快，如果算法处于早期，采用较大的step，将会使算法的收敛速度较快，且跳出局部极值的能力也更强；反之，如果在算法运行早期采用较小的step，则会使算法的收敛速度变慢，且跳出局部极值约束的能力变差。

在算法的后期，因为已经基本确定了最优解的搜索范围，则应选择较小的step，以提高算法的最终求解精度，避免由于过大的步长使算法跳过了优质解，所以这种动态措施要优于固定step的机制[3]。经过上述分析，可以知道，在鱼群算法的早期应采用较大的step值，而在后期应逐渐收敛到较小的step值。设step的取值范围为[stepmin，stepmax]，设定其变化规律为公式3。根据该模型，可得步长step的调整公式4。

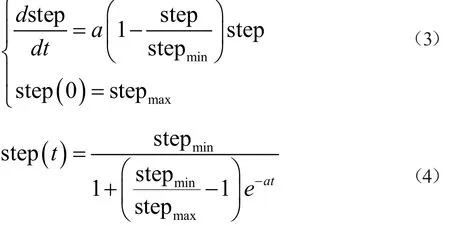
根据经验可设置visual和step两个值的取值范围。通常visual的取值在1～10；step的取值在0.5～8；a设为100。

2 算法实现

动态自适应人工鱼群算法（Dynamic Adaptive Artificial Fish Swarm Algorithm，DLAFSA）

输入：规模为N的种群。

输出：最佳个体Xgbest(t)。

步骤1：初始化算法参数，包括种群规模、视野最大值及最小值、步长最大及最小初始值、尝试次数。迭代次数设置t=0。

步骤2：在解空间内对鱼群采用随机机制进行初始化。

步骤3：扫描种群，取出当前最优解Xgbest(t)，写入公告板。

步骤4：鱼群中全部个体执行随机自由游动，并更新各自的自身状态Xi(t)。

步骤5：鱼群内个体在各自的视野visual内执行觅食行为。

步骤6：鱼群内的个体执行聚群操作。

步骤7：鱼群内的个体执行追尾操作。

步骤8：对visual和step分别按照公式2和4进行修正调整。

步骤9：更新公告板，迭代计数器t=t+1。

步骤10：若算法满足终止条件，则输出公告板上的最优解Xgbest(t)，算法结束。否则，如果算法进入后期，则随机淘汰种群内的10%的个体，然后在解空间上，再以Xgbest(t)为中心，以2×visual为半径的范围内，随机生成10%的个体，并跳转到步骤4。

3 仿真实验和结论

将DLAFSA算法与标准人工鱼群算法应用C语言进行编码实现，并对两个算法进行实验对比。采用8个经典Benchmark函数进行测试，8个函数分别是：Sphere函数f1(x)、Griewank函数f2(x)、Rastrigin函数f3(x)、Ackley函数f4(x)、Rosenbrock函数f5(x)、Schwefel函数1f6(x)、Quartic函数f7(x)、Schwefel函数2f8(x)。

从测试数据可以看出，对于所有测试函数来讲，在f1和f6两个函数上，两种算法均能获得最佳解，在其他6个函数上，两个函数均没有获得最佳解，但是对比两个算法所获得的解平均值和解方差来看，改进之后的算法明显优于标准人工鱼群算法。表1列出了两个算法在8个测试函数上的收敛成功次数和收敛成功时所需的平均迭代次数，从表1数据可以看出，改进后的自适应人工鱼群算法在8个函数上的收敛成功次数要明显大于标准人工鱼群算法，其所需迭代次数也明显小于标准人工鱼群算法。基于以上数据的对比可以得出结论，改进之后的DLAFSA较AFSA能更好地保证全局搜索和局部搜索的平衡。

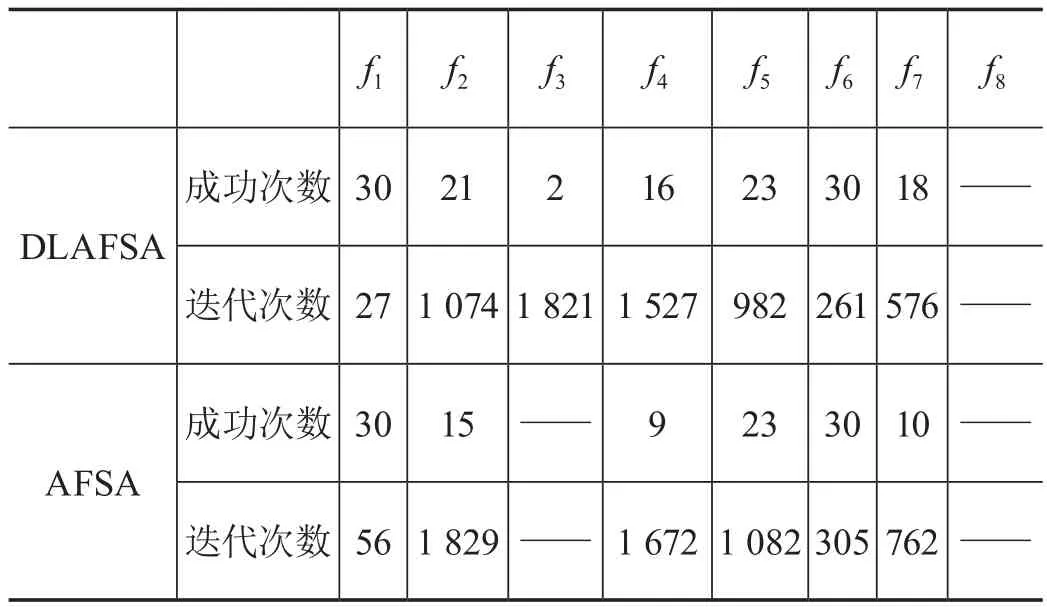
表1 DLAFSA与AFSA在Benchmark函数上的成功次数迭代次数比较

本文通过引入Logistic模型，使人工鱼群算法的两个重要参数—步长和视野实现动态自适应调整，使鱼群中的个体在早期具有较大的步长和较宽阔的视野，以保证算法具有较快的收敛速度和较广阔的搜索范围，而在后期逐渐转入精细的局部搜索，使算法的解精度得以提高。最终实验结果表示：动态自适应人工鱼群算法的解精度明显优于标准人工鱼群算法。