基于磁感应的油藏裂缝内地下无线传感网络定位*
2018-12-26郭会军李维勤林遂芳
郭会军,李维勤,林遂芳
(西安理工大学自动化与信息工程学院,西安 710048)
目前全球能源处于石油向清洁能源过渡的时代,原油和天然气在世界一次能源消费结构中占比呈下降趋势(仍超过50%)。但是随着能源需求的不断增长,再加上较低的油藏采收率(≤60%),可用的油藏消耗速度仍然日益加快。在节能减排的背景下,提高油藏的采收率对于保障能源安全具有重要意义[1]。
提高采收率需要对油气田开发管理规划和开采工艺措施进行优化,需要实时获取整个油藏的物理化学参数,如压力、温度和流体类型等,但是目前尚缺乏能直接深入油藏内部进行实时在线监测的有效手段。考虑到油藏开发中常运用水力压裂技术在井筒和目标岩层之间产生若干既窄又长的裂缝,作为油藏和井筒之间的流体通路,通讯方式和定位穿过裂缝进入油藏的传感器节点成为实现分布式测量的难点。文献[2]于2006年首次提出了基于磁感应通信的地下无线传感网络,开辟了研究油藏参数分布式测量的新领域。此后,学者们在传感器的微型化、节点无线充电、信道建模、通信协议和节点定位等方面展开了研究工作,其中节点定位是否准确是制约实施油藏参数分布式测量的重要环节[2-5]。
地下无线传感网络中,环境和通信距离的限制使得锚节点整体比例很低,传感器节点邻居锚节点数往往少于3个以至没有,常规无线传感网络节点定位方法[6-8]已无法适用这种情况。此外,节点间距离估计还受线圈方向、节点周边外界磁场变化等因素影响[9]。为此文献[10]研究了2-D环境下信标位置固定,基于磁感应通信的移动节点定位。文献[11]研究了2-D环境下参考节点位置固定,基于阻抗测量的节点定位。文献[12]采用3方向通信线圈,研究了3-D环境下地下无线传感网络的节点定位,并且采用了极大似然函数来估计节点位置。文献[13]通过半定规划结合共轭梯度法SDP+CGA(Semi-Definite Programming Enhanced Conjugate Gradient Algorithm)的优化计算,得到随机分布的基于磁感应通信的地下无线传感网络的节点位置。但是上述方法不仅误差普遍较大,而且应用条件严格,不便于实际使用。同时油藏环境特殊不适宜在其内布置锚节点,锚节点比例偏低使得定位问题更为复杂。
考虑到油藏裂缝中节点定位的特殊性,本文提出了一种基于接收信号磁感应强度的两步式节点定位方法。文中两个锚节点部署在井筒,传感器节点随机分布在裂缝内,节点间均采用三方向线圈天线通信,节点距离依据接收磁感应强度进行估计。然后将定位转换为半定规划问题,采用可变方向增强拉格朗日方法ADM(Alternating Direction Augmented Lagrangian Method)进行求解,在此基础上引入粒子群优化算法在节点小邻域内精细搜索获得最优定位,最后通过仿真对算法的性能进行了分析比较。
1 根据磁感应强度测量节点间距离原理
水力压裂技术产生的裂缝长度通常可达100 m,宽度和长度分别为0.01 m和1 m。为了对油层进行分布式测量,微纳传感节点混在携砂液中(含石英砂)随压裂进程进入裂缝,其在裂缝中的位置因而是随机分布的[4]。体积和功率较大的锚节点通常布置于井筒内部,由外部电源供电,可直接与裂缝内的传感器节点进行磁感应通信,锚节点同时通过磁感应方式为传感节点提供电能;微纳尺寸的传感器节点具有全向线圈天线,同时配置超级电容器储存耦合电能。考虑到供电及传感器通信能力等因素,在面向油藏裂缝的地下无线传感网络中,锚节点和传感节点之间通信(下行链路)是单跳方式,传感节点与锚节点之间通信(上行链路)采用多跳方式[5]。
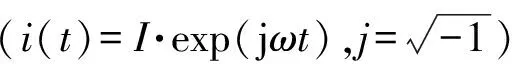
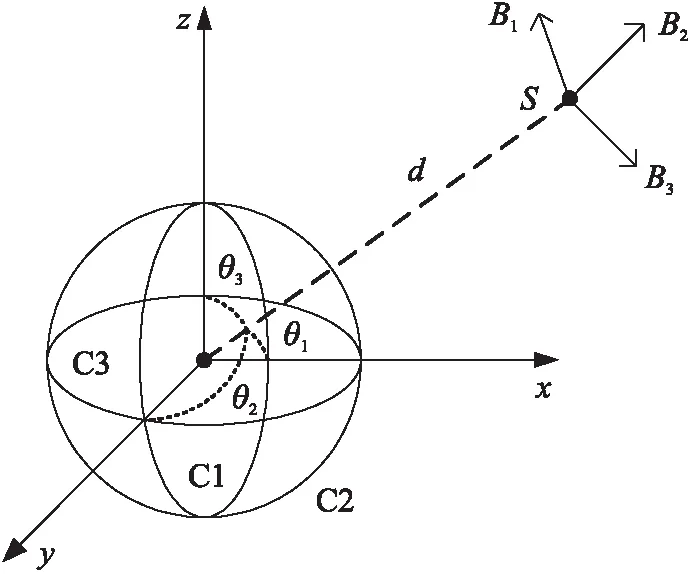
图1 发射线圈及其磁场
令Bk表示第k个发送线圈在节点S处产生的磁通密度,θk表示S与xyz轴的极角。当距离d远大于4倍的线圈半径时,S处的磁通密度为
(1)
式中:Bkr与Bkt分别表示磁通密度的径向和轴向分量,μ是磁导率。M表示电流所产生磁矩的幅值,可由下式确定
M=NIAF
(2)
式中:N和A分别表示线圈的匝数和线圈的面积,F表示垂直线圈所在平面的单位矢量。
由式(1)可知总的磁通密度Bk为
(3)
将式(3)两边平方且代入式(1)可得
(4)
式中:
(5)
假设已知Bk,则
(6)
同时S的3个极角满足
cos2θ1+cos2θ2+cos2θ3=1
(7)
将式(6)代入式(7)可得
(8)
则距离d可表示为
(9)
当3个发送线圈具有相同的磁矩幅值,即Mk=M时易知Ck=C,则式(9)可简化为
(10)
令
(11)
则最终的距离估计简化为
(12)
而在S处,第k个发送线圈产生的磁通密度被3个接收线圈测量,其值为
(13)
式中:下标1,2,3表示互相正交的3个接收线圈,当忽略损耗时易得
Bkx=Bk
(14)
可知3个接收线圈测量的磁通密度为常值,与其方向无关,从而有利于节点布置。这样根据接收线圈的磁场测量值由式(13)和式(12)即可确定其与锚节点之间的距离,节点之间距离也可采用这种方式测定。
2 基于ADM的节点初始定位
2.1 节点接收信号磁通密度的估计
考虑在水力压裂产生的裂缝中存在N个位置随机的传感器节点{xi∈R2:1≤i≤N},同时存在K个位置已知的锚节点{ai∈R2:1≤k≤K}。令传感器节点i与其邻居节点NHi之间距离为
{dij∈R:1≤i≤N,j∈NHi}
(15)
传感器节点i与锚节点之间的距离为
{dik∈R:1≤i≤N,1≤k≤K}
(16)
令Brms1,…,Brmsn表示传感节点接收的n个磁通密度信号样本,假设它们是独立同分布均值为(方差为(2的高斯变量。定义如下似然函数
(17)
其对数型似然函数为

(18)
则均值θ的极大似然估计为
(19)
简单推导后可得
(20)
上式表明可以从m个接收信号样本中对参数(进行极大似然估计,估计结果实际为m个接收样本的均值,且为无偏估计。基于接收信号强度(的无偏估计,根据式(12)可对收发节点之间的距离d进行估计。
2.2 节点定位问题的半定规划表示
定义传感器节点i与邻居节点j之间距离估计误差,传感器节点i与信标节点k之间距离估计误差分别为
(21)
(22)
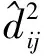
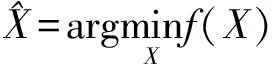
(23)
易知f(X)为凸函数[14],半定松弛之后将其转化为如下的半定规划问题
(24)

(25)
Y-XTX0
(26)
式中ei和ej为单位列矢量,I表示单位阵,Y∈RN*N为实对称矩阵。
2.3 基于ADM的节点初始定位
式(24)所示半定规划属于高维问题,约束条件数目趋近待优化参数的阶数,基于内点的传统迭代法求解时不仅计算时间长而且存储繁琐,文献[14]指出ADM方法能够在求解高维半定规划问题的同时,大幅减少计算量和存储需求。为此将式(25)重新整理为如下的矩阵形式

(27)
式中:
(28)
(29)
(30)
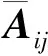
(31)
此时A(Z)为Z的线性映射,同时定义
(32)
则原问题转化为如下二次型半定规划问题

(33)
假设矩阵A行满秩,定义如下增强拉格朗日函数
(34)

(35)
(36)
(37)
迭代若干步后,即可获得全部节点位置的初步估计值,而关于算法的全局收敛可参考文献[15]。
3 基于粒子群算法的精确定位
上述半定规划将求解从低维空间转化到了高维空间,ADM算法获得的解与真实值之间仍然存在相当的误差[13,15]。为了获得更好的位置估计,有必要引入更为精细的寻优算法。倘若在以ADM算法所获估计值为圆心,半径不超过节点通信半径的圆形区域内进一步搜索寻优,有可能获得误差更小的位置估计。相比其他搜索寻优算法,粒子群算法PSO(Particle Swarm Algorithm)在具有较强的搜索能力的前提下,涉及参数较少且实现简单[16],适宜用于本文所述情形。
定义如下目标函数
(38)
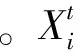
(39)
(40)
(41)
4 仿真分析与性能评估
采用MATLAB对本文算法进行了仿真和验证,并与ADM+CGA算法结果进行比较。两个锚节点布置在钻井井筒中固定位置,传感器节点随机散布在裂缝中,裂缝内部没有锚节点。如前所述水力压裂工艺产生的裂缝宽度很小,混在携砂液(起支撑裂缝作用)进入裂缝内部的传感器节点定位问题等效为平面内节点定位问题。为了研究噪声引起的磁场测量误差对定位的影响,利用距离测量误差取代磁场测量误差,观察相对定位误差随距离测量误差的变化。引入噪声因子nf∈[0,1]反映距离测量噪声方差大小,包含测量误差的距离估计可表示为
(42)
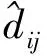
(43)


表1 仿真参数
在nf=0.5和传感器节点数为50的情况下,首先采用ADM算法进行了初始定位,结果如图2所示,可见存在较显著的定位误差(ERA=6.923 7)。而后以ADM定位作为初值,分别采用CGA算法和PSO算法进行了精确定位。图3和图4分别为CGA算法和PSO算法定位结果,其相对定位误差分别为0.577 1和0.587 1,与图2对比可见定位精度获得显著提升。
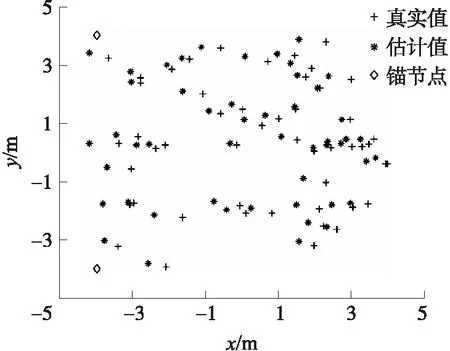
图2 ADM算法定位
然后在不同的传感器节点数量(传感器节点从50~100,步长10)和不同的距离测量噪声强度nf(0.05~0.60)的情况下,观察本文算法和ADM+CGA算法的相对定位误差,结果如图5和图6所示。
图5表明在锚节点数量为2,通信距离固定条件下,ADM+CGA和ADM+PSO算法的定位误差随着传感器节点的增加均呈下降趋势,ADM+PSO算法略优于ADM+CGA算法。从图6可以看出,在锚节点为2,传感器节点为60,通信距离为3.2 m场景下,随着噪声强度从低到高的增加,ADM+CGA和ADM+PSO算法的定位误差均逐渐变大,但是ADM+PSO算法结果仍优于ADM+CGA算法。
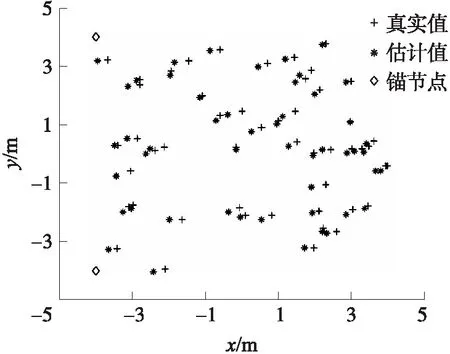
图3 ADM+CGA算法定位
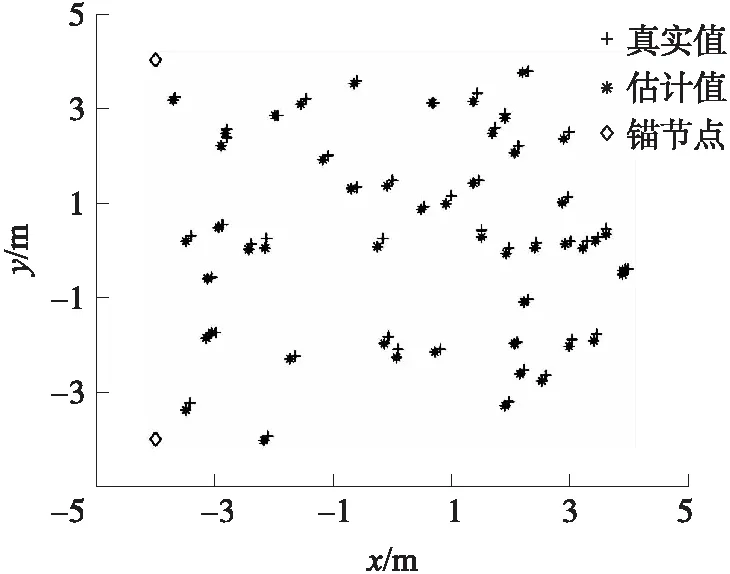
图4 ADM+PSO算法定位

图5 相对定位误差随传感器节点数变化

图6 相对定位误差随噪声变化
5 结论
对于锚节点布置在井筒,传感器节点随机分布于油藏裂缝条件下的地下无线网络节点定位,可从节点接收信号的磁感应强度中估计出其与邻居节点和锚节点的距离,在此基础上将定位问题转换为半定规划问题,利用变方向增强拉格朗日方法和粒子群优化算法结合的方法可获得较好的定位结果。仿真结果也表明,本文方法优于ADM+CGA方法。
