原子钟在线监测评估方法设计

2018-12-26邓小波

无线电工程 2018年1期

关键词：原子钟稳定度时频

邓小波，赵斌，王铮

(1.兰州大学资源环境学院，甘肃兰州 730000；2.中国人民解放军61711部队，新疆喀什 844000；3.中国电子科技集团公司第五十四研究所，河北石家庄 050081)

原子钟在线监测评估方法设计

邓小波1,2，赵斌2，王铮3

(1.兰州大学资源环境学院，甘肃兰州 730000；2.中国人民解放军61711部队，新疆喀什 844000；3.中国电子科技集团公司第五十四研究所，河北石家庄 050081)

大型通信、测量电子系统一般配备2台或2台以上原子钟作为系统的时间、频率基准，互为备份构建主、备时频信号基准，以提高系统时频信号可靠性，保障系统连续运行。主备原子钟间虽然可通过相位比对、数据分析检测到原子钟工作状态异常状况，但是由于缺乏参考，难以通过时频系统本身区分故障来源，存在故障定位难的技术难点。针对这一问题，提出了一种基于中间振荡器的主、备用原子钟频率跳变检测、短期稳定度分析评估方法，为时频系统主、备用原子钟故障定位提供技术手段，提高时频系统故障判断准确性，并缩减系统故障定位、故障恢复时间。使用3台铷原子钟进行了测试验证，实验结果表明，该方法可实现时钟稳定度的评估，并可实现时钟频率跳变的故障定位。

原子钟评估；稳定度评估；频率跳变检测

0 引言

在通信、测量电子系统中，时间频率系统作为通信、测量系统的时频基准，为其他功能子系统提供稳定、准确度时频信号，而原子钟作为时频子系统的频率信号根源，其工作状态将直接影响工作性能。原子钟的主要性能指标包括频率准确度、频率漂移率和频率稳定度指标，通过以往的工程经验，原子钟的故障主要是其物理器件故障，如真空度下降、铷泡故障等原因导致原子钟失锁，输出频率发生跳变，直接影响输出信号的准确度与稳定度[1]。

在系统运行过程中，为保证系统运行的稳定性、可靠性，在时频系统设计时，多采用双机热备的双原子钟设计方案，并通过相位比对设备检测主用、备用原子钟间相位差值，当相位差值发生跳变时，可判断原子钟出现故障。然而对于故障的定位，由于缺乏参考输入，无法直接判断故障发生位置为主用原子钟或备用原子钟，往往需要通过系统运行功能、性能状态来判断主用或备用原子钟故障，具有较大的滞后性，无法在原子钟故障初期本文发现并定位故障[2-3]。虽然配备双热备原子钟，却无法保障时频子系统服务的连续性高质量服务，因此提出了增加一个中间振荡器作为参考频率源，通过主、备用原子钟与中间振荡器的相位差值，采用三角帽法计算时钟频率稳定度，采用最小二乘法进行频率跳变监测与故障源定位，在系统设计成本增加不大的前提下为原子钟性能评估、原子钟故障定位提供数据支持与技术手段。

1 系统总体设计

在主用原子钟A、备用原子钟B间引入中间振荡器C，使用相位比对设备对原子钟A、B及中间振荡器C输出频率信号进行相位比对，依据相位比对数据对3路时频信号进行频率稳定度评估、频率跳变检测，保障时频系统的高可靠性运行[4]。其中，中间振荡器可依据系统监测性能、成本需求灵活选用铷原子钟或恒温晶振。系统设计框图如图1所示。

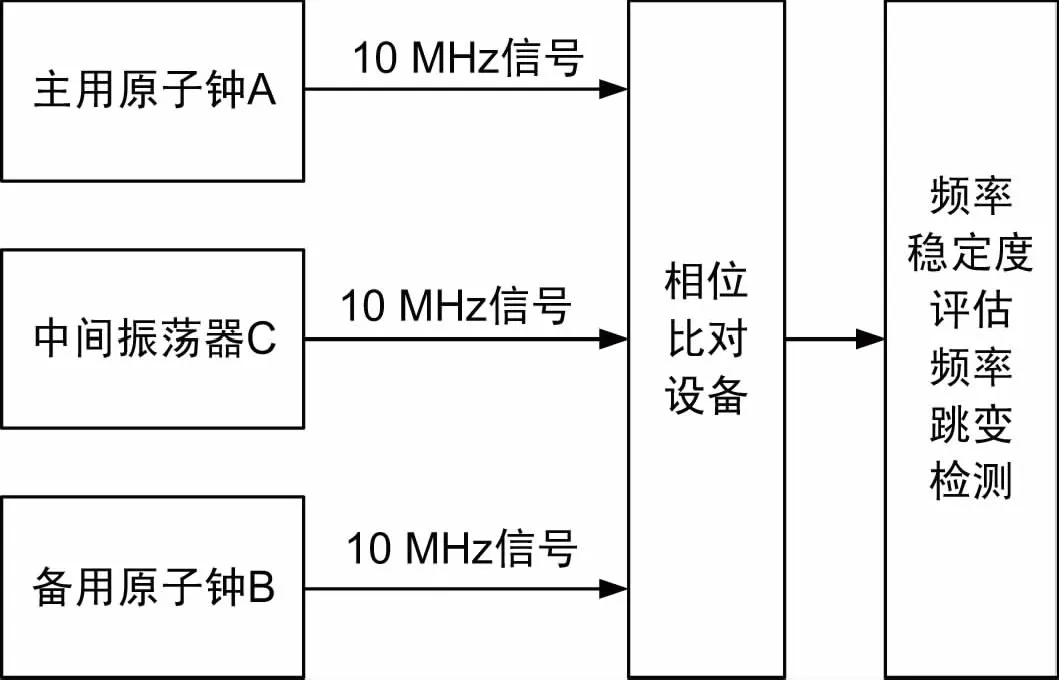
图1 基于中间振荡器的时频在线监测系统

2 基于三角帽法频率稳定度评估

频率稳定度表征频率源输出频率信号准确度的变化程度，一般采用方差表征数据集合的稳定度，原子钟频率稳定度评估一般采用阿伦方差对原子钟相位信号进行采集计算，测量方法为使用高于被测频率信号稳定度1个数量级的频率信号作为参考[5]。

Allan方差公式为：

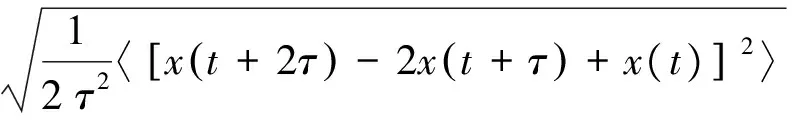
式中，x(t)为时钟在t时刻的相位值；τ为取样间隔；〈〉代表求平均值。

在实际系统运行过程中，不具备更高稳定度级别的参考时钟信号，无法针对时钟频率稳定度进行直接测量，为实现针对主、备用原子钟的频率稳定度评估，引入中间振荡器，采用三角帽法进行主、备用原子钟及中间振荡器的频率稳定度评估[6]。

通过测量时钟a和b间相位差值，可计算a和b时钟的相对频率稳定度ADEVabτ。

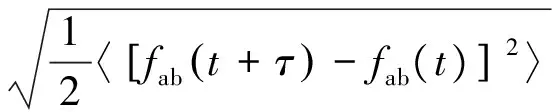
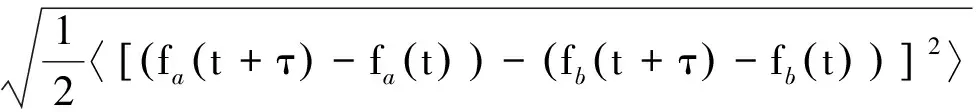
由于a和b时钟为独立运行时钟，因此可得

由此可得，

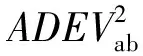
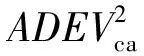
式中，ADEVabτ、ADEVbcτ和ADEVcaτ可通过时差测量运算直接获得，通过解算可以获得：

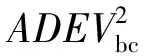
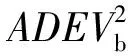
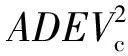
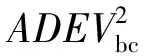
因此通过实时在线测量主/备用原子钟、恒温晶振的相差信息，可通过三角帽法解算时钟的频率稳定度指标，当任意时钟稳定度恶化时，可快速定位故障时钟源，并依据系统需求进行主、备原子钟切换，保证后端设备使用。

3 基于最小二乘法的频率跳变检测

频率准确度是指被测信号实测频率fx与其标称频率f0间的频率偏差程度，频率准确度公式为：

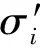
由于系统运行过程中缺乏高准确度的测量参考时钟，无法直接计算评估时钟频率准确度，只可计算时钟间相对频率准确度，通过实时测量主、备原子钟间相对频差、主/备用原子钟与中间振荡器间相对频差，利用最小二乘法对主/备用原子钟与中间振荡器间相位差值进行最小二乘法频率计算[9]，并实时比对实时测量值与最小二乘法预测值间的频率差值，当频率测量值超限时，针对超限情况进行判断，即可判定频率跳变来源。

基于最小二乘法的频率跳变检测原理如图2所示。

图2 基于最小二乘法的频率跳变检测原理

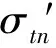
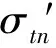
通过比较ΔΦ与预设门限值，即可监测时钟跳变情况，当发生预测值残差超限时，可依据三角闭合法进行判断跳变来源，若ΔΦab、ΔΦac发生超限，而ΔΦbc未发生超限，则可判断时钟a发生频率跳变。

4 时钟在线评估系统实验验证

在实际项目应用中使用3台铷原子钟进行时钟的在线监测评估，使用多通道比相仪进行时钟a、b和c间的相位比对，使用三角帽法、最小二乘法频率跳变监测算法进行相差数据处理[5]，为体现评估与跳变监测系统能力，其中a、c原子钟正常运行，b原子钟在数据采集开始时进行了开关机，相位数据处理结果如图3和图4所示[11-12]。

通过数据分析，可发现时钟a、c稳定度指标相对较高，同时通过最小二乘法时钟相位预测残差示意图(如图5所示)也可分析，时钟b在150 s、550 s位置发生2次残差值跳动，依据前面所述的故障定位方法，发现时钟ab与时钟bc间相位预计残差跳动，因此定位故障为b原子钟发生了频率跳变，传统主、备相位比对图5中时钟ab相位预测残差，发现时钟ab间相位预测残差发生跳变，无法依据测量值定位故障源，仅可依靠后续用时设备指标变化反推时钟跳变源为主、备原子钟，而采用中间振荡器的原子钟在线监测与评估方法则可迅速定位故障为时钟b发生频率跳变，导致其稳定度下降，完成了b时钟失锁的故障检测[13-14]。

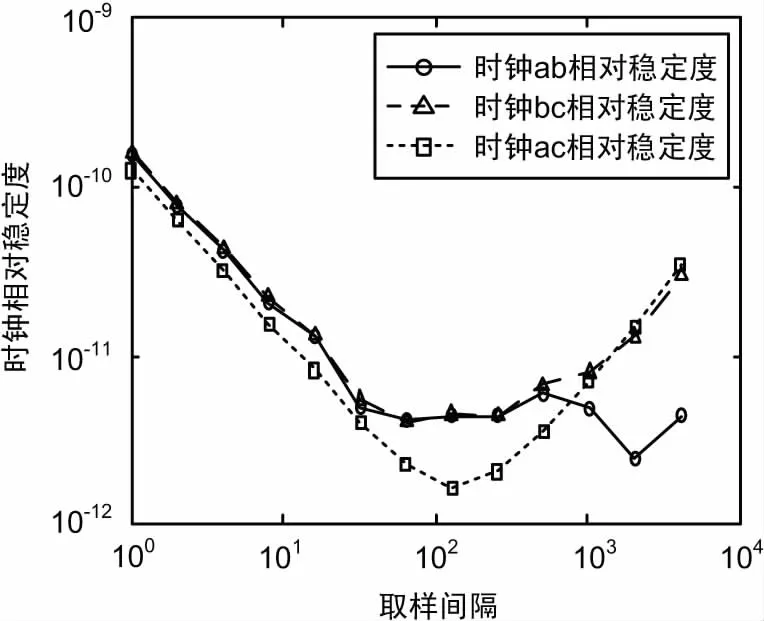
图3 时钟相对频率稳定度示意

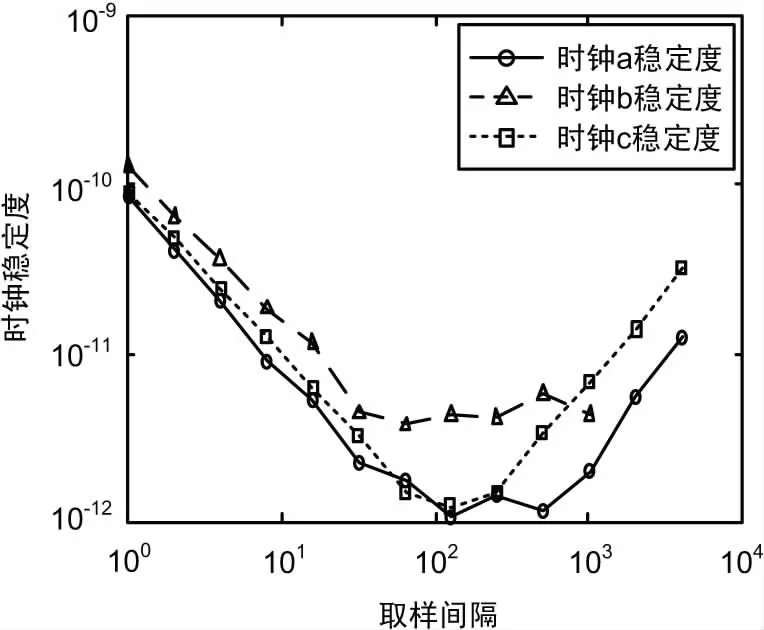
图4 时钟稳定度示意

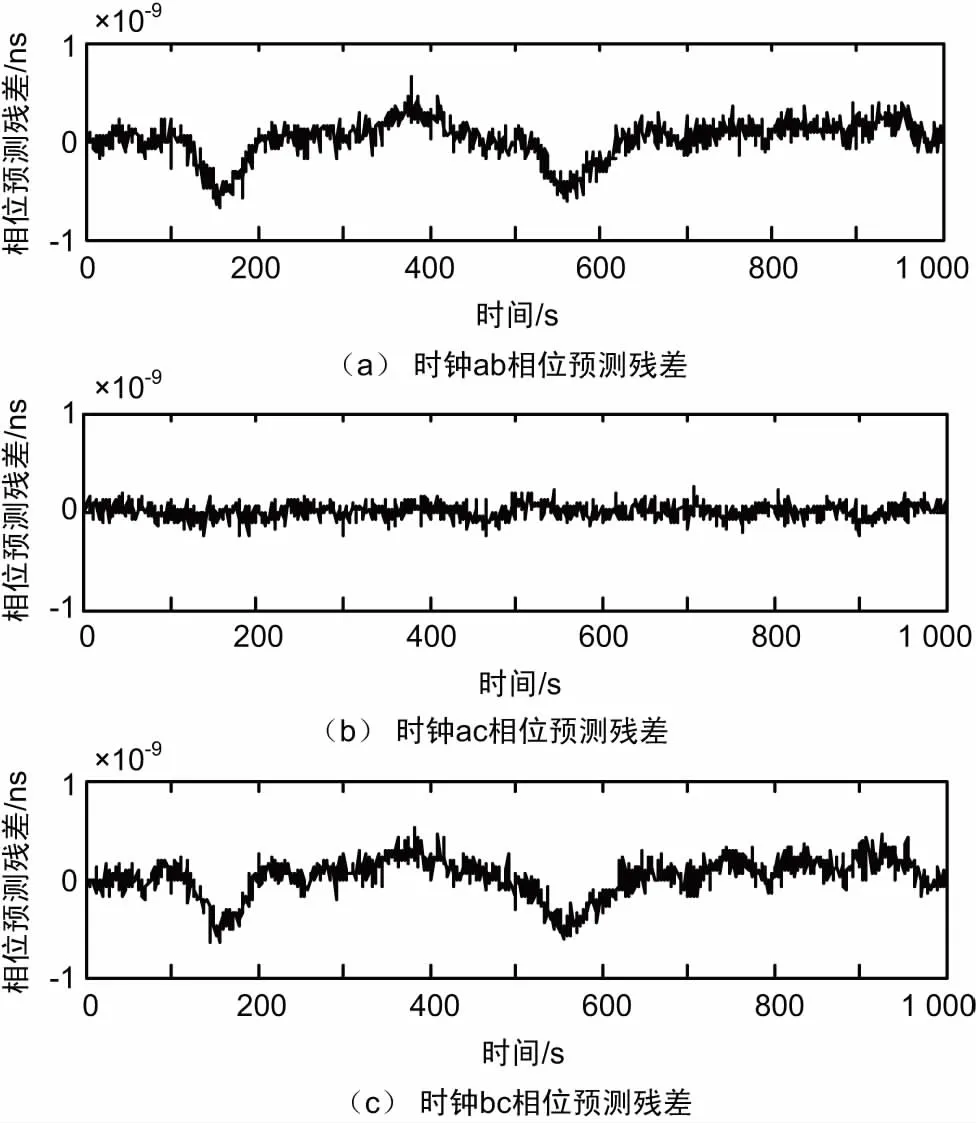
图5 最小二乘法时钟相差预测残差示意

5 结束语

本文针对时间频率系统原子钟在线评估，介绍了相关原子钟性能指标评估的模型与算法，并基于三角帽法稳定度评估、最小二乘法时钟频率跳变检测进行了实验验证。实验验证结果表明，采用增加中间振荡器的时频系统在线评估构架可有效针对原子钟稳定度、原子钟频率跳变进行在线评估、监测，并可为故障定位提供数据手段，增加时间频率系统工作可靠性，降低故障定位和故障恢复时间。

[1] 李孝辉,杨旭海,刘娅，等.时间频率信号的精确测量[M].北京：科学出版社,2010:104-144.

[2] 应展烽，吴军基，易文俊.基于小波变换和三点法的基波频率测量[J].电机与控制学报，2010，14(2)：65-70.

[3] 卫国.频率源的时域噪声特性分析[J].中国科学,1992(10)：1096-1102.

[4] 郭海荣.导航卫星卫星钟时频特性分析理论与方法研究[D].郑州：解放军信息工程大学，2006.

[5] 赵娜，胡彩波，赵伟，等.卫星钟及其性能监测与故障处理[J].无线电工程，2012，42(4):30-33.

[6] SESIA I,GALLEANI L,TAVELLA P.Implementation of the Dynamic Allan Variance for the Galileo System Test Bed V2[C]∥Proceedings of IEEE EFTF-FCS,2007:946-949.

[7] GALLEANI L,TAVELLA P.An Algorithm for the Detection of Frequency Jumps in Space Clocks[C]∥Proceedings of 42nd Annual PTTI,2010:503-508 .

[8] 李孝辉.卫星导航系统时间流测试[C]∥中国天文学会,2014年学术年会论文集,2014.

[9] 李玮.卫星导航系统时间测试评估方法研究[D].北京：中国科学院研究生院(国家授时中心),2013.

[10] 李作虎.卫星导航系统性能监测及评估方法研究[D].郑州：解放军信息工程大学,2012.

[11] 潘小培,屠鲁征,罗定昌.综合原子时及其结果分析[J].中国科学,1988(8)：851-860.

[12] 卫国.原子钟时间尺度的稳定性分析[J].中国科学,1922(1)：80-86.

[13] HUANG Xinming,GONG Hang,YANG Wenke,et al.AnItegrity Monitoring Algorithm for Satellite Clock Based on Test Statics[C]∥Proceedings of China Satellite Navigation Conference,2012:515-526.

[14] 吴守贤,漆贯荣.时间测量[M].科学出版社,1983：112-118.

DesignofOnlineMonitorandEvaluationMethodforAtomicClock

DENG Xiaobo1,2,ZHAO Bin2,WANG Zheng3

(1.CollegeofEarthEnvironmentalSciences,LanzhouUniversity,Lanzhou730000,China;2.Unit61711,PLA,Kashi844000,China;3.The54thResearchInstituteofCETC,Shijiazhuang050081,China)

Large-scale communication and measurement systems normally have two or more atomic clocks to form a master-slave time and frequency reference,which increases the system reliability and ensures continuous operation.Although the abnormal state of master and slave clocks can be detected by measuring their phase difference,but it’s hard to identify the source of fault due to the lack of external reference.In order to solve this problem,the paper proposes a master-slave clock frequency jump detection and stability evaluation method based on middle oscillator.This method can improve the fault detection accuracy of time frequency system and reduce the fault location and recovery time.Three Rb clocks are used in experiment to verify this method,and the result shows that the method can successfully evaluate the clock stability and identify the fault source.

atomic clock evaluation；stability evaluation；frequency jump detection

2017-09-15

中国电子科技集团公司航天信息应用技术重点实验室基金资助项目(EX156290055)

10.3969/j.issn.1003-3106.2018.01.10

邓小波，赵斌，王铮.原子钟在线监测评估方法设计[J].无线电工程,2018,48(1):46-49.[DENG Xiaobo,ZHAO Bin,WANG Zheng.Design of Online Monitor and Evaluation Method for Atomic Clock[J].Radio Engineering,2018,48(1):46-49.]

TN967

1003-3106(2018)01-0046-04