输电线横风向动张力理论分析与试验研究

汪 伟，孙成丽，汪 睿

(1.武汉理工大学土木工程与建筑学院，武汉 430070；2.武汉理工大学理学院，武汉 430070；3.武汉地铁集团有限公司，武汉 430035)

由于架空输电线缆空间跨距大、截面小、自身轻柔、且结构阻尼小，因此成为了一类典型的风敏感结构。在风工程领域中，一般将风荷载可以看作两部分的组合，分别为平均风和脉动风，平均风周期长，而脉动风周期很短。并且把平均风的作用看成静荷载，把脉动风的作用看成动荷载。在各种风振响应中，由脉动风引起的导线的抖振响应是抗风设计的关键。

导线风致响应可以分为静风荷载作用下的静力响应和静平衡状态处脉动风引起的动力响应。在较高的风速下，导线平面的静力变形和风偏非常显著，这也使得导线张力从初始状态发生了相当大的变化，从而导致了系统动力特性的变化。Irvine[1]最先系统地开展了柔性索结构的理论分析，详细阐述了两端固定索的静、动力特征及响应的计算方法。国内学者马星等[2]利用Irvine的理论解析解，建立起输电塔线线性体系的耦合振动方程。Wang等[3]给出了输电线风振响应的理论计算方法，指出了平均风偏的非线性静力状态及气动阻尼对输电线三维动张力的影响尤为重要。Loredo-Souza和Davenport[4]比较了使用基于拟静力模型的线性随机振动理论和气弹风洞试验得出的响应，结果证实了由于气动阻尼较大，背景分量在顺风向响应中占主导地位。

文章给出了弦向动张力作用的背景分量和总响应的功率谱及均方值的频域解析解。并以单跨四分裂输电线为例，通过标准气弹模型风洞试验，对已有的理论模型进行验证。从而揭示了输电线风振响应特点与规律，为更好地计算导线的风致响应提出了新的方法。

1 理论分析框架

1.1 静力响应分析

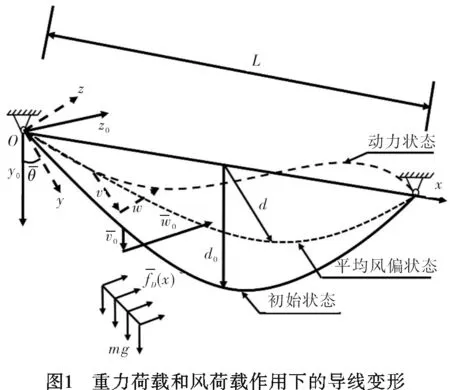
输电线两端固定在同一水平高度上，垂跨比为d0/L=1/30～1/50的均匀悬挂导线。初始状态，单位长度重力荷载为mg=q0，水平弦向张力为H0，初始位置为y0(x)，垂度为d0=q0L2/8H0，如图1所示。此研究考虑风致响应最为不利的风向，与导线垂直的方向。单位长度上的风荷载由下式给出

(1)

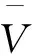
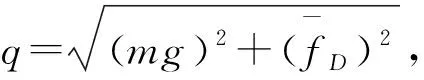
弦向张力H由下面的非线性方程确定

(2)

式中，E是杨氏模量，A是导线的面积。

1.2 背景响应分析

背景响应可以直接由影响线函数确定。对于一个给定的响应r(t),其背景分量由下式给出

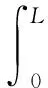
(3)

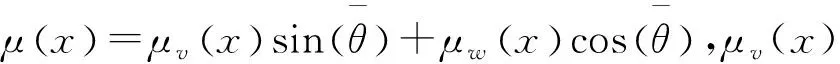
水平弦向动张力的影响线函数为

(4)

其中

(5)

背景响应的均方值可以计算为

(6)

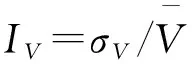
2 标准气弹模型风洞试验

2.1 试验工况与模型设计

此次风洞试验在西南交通大学XNJD-3风洞中进行，考虑到模型和风洞实验室的尺寸以及模拟紊流边界层尺寸等要求，模型几何相似比为λl=1∶50。为了使试验结果有代表性，此次试验导线型号为JL/G3A-1250/125，其参数如表1所示。

表1 导线原型参数

根据气弹模型的相似准则，确定模型的各项标准缩尺比参数，如表2所示。

表2 导线模型相似比

此次试验输电线模型为单跨四分裂，跨度为10 m，对应实际跨长500 m，两端铰支。考虑风致响应最为不利的风向角，即垂直于导线90°方向。风速为2.8 m/s、4.3 m/s、5.7 m/s、7.1 m/s共4种工况，对应实际风速分别为20 m/s、30 m/s、40 m/s、50 m/s。

2.2 试验动张力分析

利用上述理论模型计算背景响应，并将其与试验背景响应和试验总响应进行对比，对比结果见表3、图2～图5。

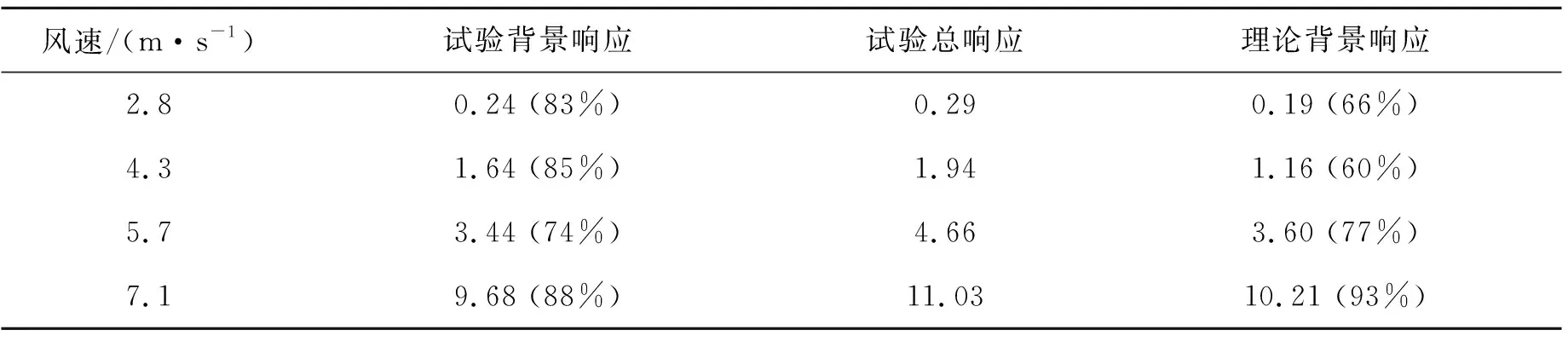
表3 各工况理论与试验响应均方值(×10-2)

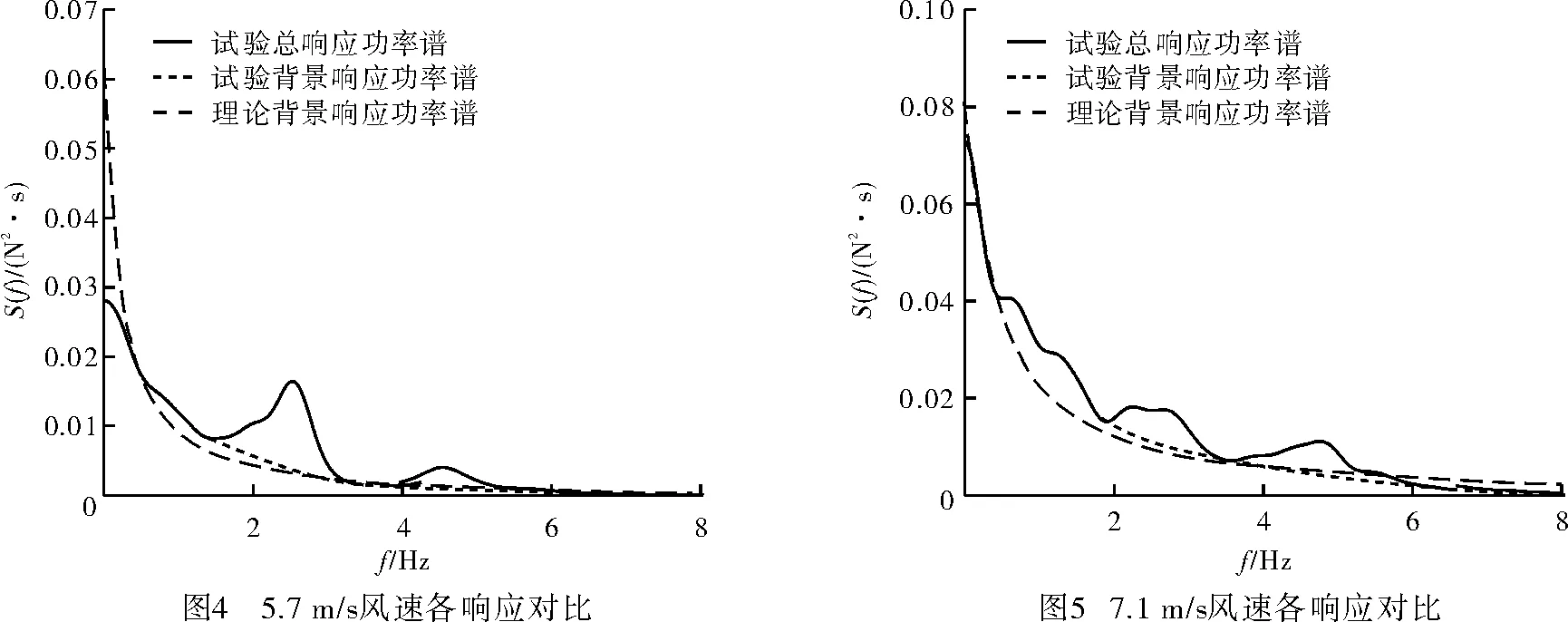
由图形和表可以看出，动力响应以背景响应为主。影响线方法计算的背景分量的均方值和功率谱曲线都能和试验测得的结果吻合良好，试验测得的弦向动张力背景响应占试验总响应的74%～88%，理论算得的背景响应所占比重为60%～93%，试验测得的弦向动张力背景响应略高于理论模型计算的背景响应。

3 结 论

文章研究了风荷载作用下输电线横风向动张力响应，将静力平衡状态处的动力响应分为背景响应和共振响应，背景响应通过影响线函数进行计算，并与标准气弹模型风洞试验结果进行对比。研究发现，影响线方法计算的背景分量的均方值和功率谱曲线都能和试验测得的结果吻合良好，动力响应中背景响应占主导。而且随着风速的增大，实验测得的背景响应和总响应都增大，理论计算的背景响应也随着风速的增大而增大。