冲击荷载下钢骨混凝土梁残余变形公式拟合

段圣允

(沈阳贵聚建设工程有限公司，沈阳 110020)

构件在冲击荷载下常因产生过大变形而宣布破坏，故其在冲击荷载下的变形量对于评估构件的受损程度具有重要意义。刘德源、李玉楠、瞿海雁等[1-3]基于刚塑性理论对钢管混凝土构件、钢筋混凝土构件冲击荷载下的变形进行了拟合，而钢骨混凝土梁在冲击荷载下的变形计算尚有不足，故以数值模拟结果为基础，结合刚塑性理论，考虑冲击速度、冲击质量、型钢强度、构件跨度的影响，对冲击荷载下的残余位移进行公式拟合。

1 刚塑性理论

刚塑性理论提出，冲击动能主要转化为了构件的塑性应变能，且塑性应变能主要集中在“塑性铰”区；瞿海雁[3]根据塑性铰理论，提出可以根据冲击动能与构件能量的守恒，在跨中和支座位置分别采用“塑性铰”，求出构件的转角和位移，图1为塑性铰简化模型。

冲击荷载下构件的变形经历弹性变形段、弹塑性变形段，最终进入到一个稳定变形段，产生一个稳定的变形，该变形主要由塑性应变能产生。塑性应变能EP的大小可由构件的动态塑性弯矩Md与构件的转角θ相乘得到，且塑性耗能EP与冲击动能EK之间存在着一定的比例关系，冲击荷载下的动态塑性弯矩Mdm与静荷载下的正截面受弯承载力Ms之间存在一定的比例关系

EP=Mdθ=2Mdmθ+2Mdsθ

(1)

EP=αEK

(2)

Mdm=βMs

(3)

而转角θ与残余位移Ud又满足简单的几何关系

Ud=tanθ·L/2≈θ·L/2

(4)

其中，Mdm为跨中位置的动态塑性弯矩；Mds为支座位置的动态塑性弯矩；参数α、β为比例系数，静载下的受弯承载力Ms可由文献[4]的公式进行计算。

2 构件设计

参考相关规程[4，5]设计钢骨混凝土梁，两端固定梁几何尺寸为b×h×L=180 mm×230 mm×2 000 mm。距离横截面上下25 mm放置4根三级螺纹钢；正中位置放置一根横截面尺寸为H×B×t1×t2=100 mm×100 mm×6 mm×8 mm的H型A3钢；冲击质量M=400 kg、冲击速度V=6 m/s。其余构件均在此构件基础上通过单因素改变冲击速度V、冲击质量M、型钢强度Q、构件跨度L的方式实现。

3 公式拟合

3.1 比例系数α

表1～表4显示的是不同参数对比例系数α的影响。由表可知，比例系数α随着冲击速度、冲击质量、构件跨度的增大而增大，随着型钢强度的提高而减小，且变化都较明显。它们对比例系数α的影响可引入修正系数C1、C2、C3、C4进行考虑。

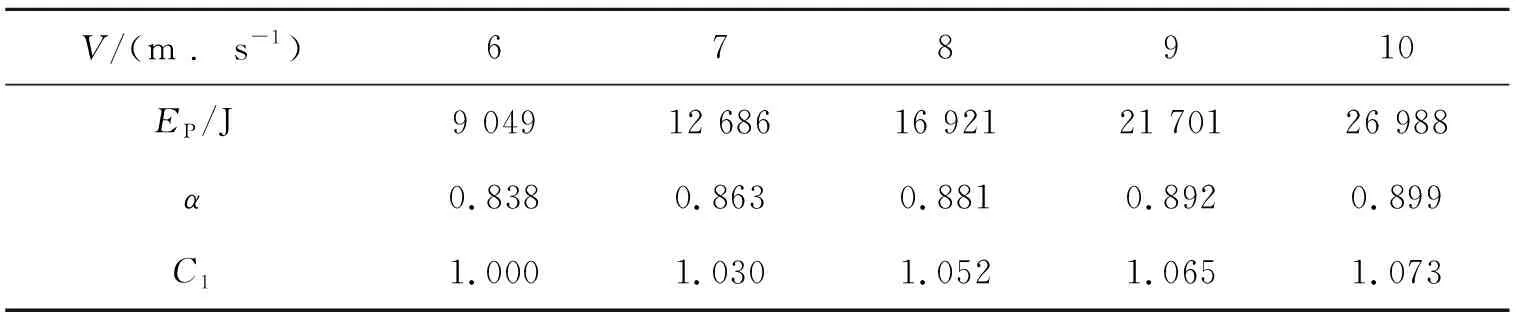
表1 冲击速度对α的影响

表2 冲击质量对α的影响

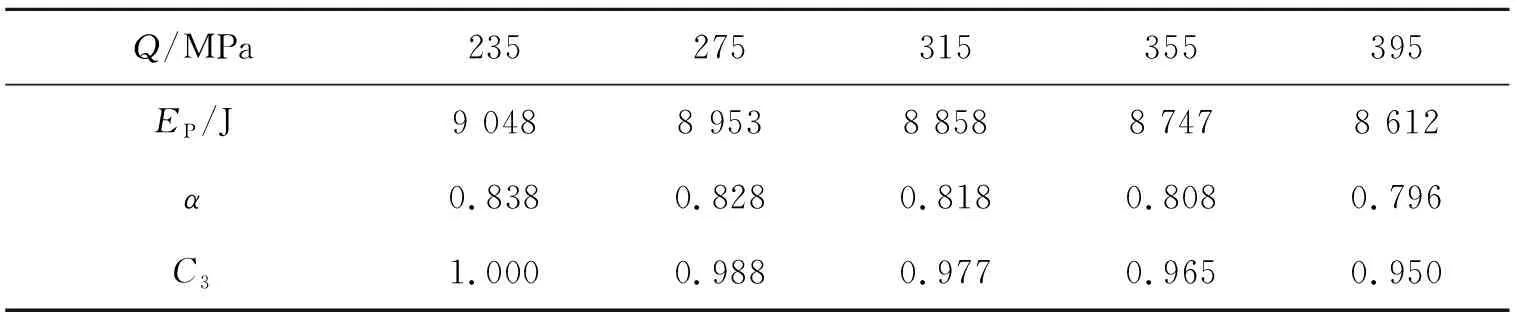
表3 型钢强度对α的影响

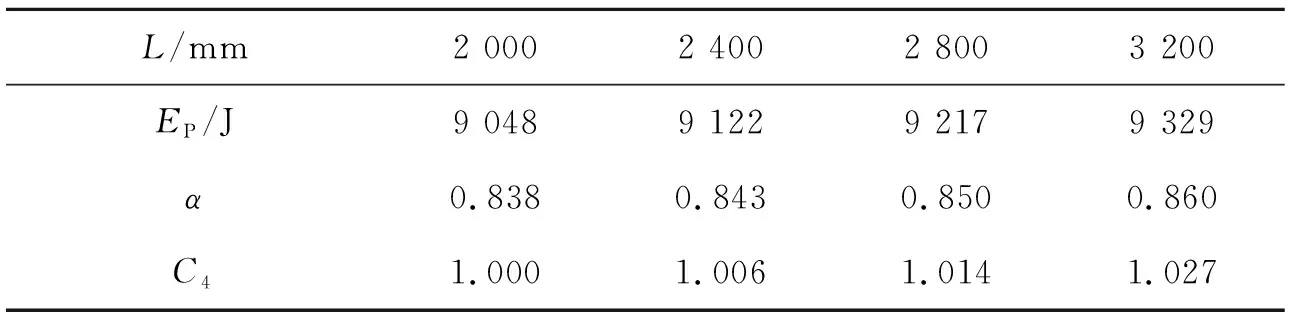
表4 构件跨度对α的影响

对表1～表4的计算结果进行数据拟合可以得到系数C1与V、C2与M、C3与Q、C4与L的函数关系

C1=0.668+0.466(V/6)-0.134(V/6)2

(5)

C2=0.909+0.094(M/600)

(6)

C3=1.073-0.073(Q/235)

(7)

C4=1.023-0.065(L/2 000)+0.042(L/2 000)2

(8)

则，侧向冲击下通过修正系数修正后的塑性耗能与初始动能关系式为

EP=0.833C1C2C3C4EK

(9)

3.2 比例系数β

由表5～表8可知，冲击速度、冲击质量、型钢强度下的跨中弯矩与支座弯矩比值变化极小，为计算方便可把Mdm/Mds比值取为定值1.2；但构件跨度对该比值的影响较大，需考虑构件跨度对比值的影响，引入修正系数E4对其进行修正。

冲击速度、冲击质量取不同值时，比例系数β的波动较小，仅在1.421～1.396、1.421～1.437范围内变化，故可忽略冲击速度、冲击质量对比例系数β的影响；型钢强度和构件跨度对β的影响可通过修正系数D3、D4进行考虑。

修正系数E4与构件跨度L的拟合公式为

E4=1.268-0.348(L/2 000)+0.079(L/2 000)2

(10)

则，跨中动态塑性弯矩Mdm与支座动态塑性弯矩Mds的关系为

Mdm=1.2E4Mds (11)

表6 冲击质量对β的影响

表7 型钢强度对β的影响

表8 构件跨度对β的影响

由表5～表8的相关数据通过拟合处理可得到修正系数D3与型钢强度Q、修正系数D4与构件跨度L的关系式

D3=1.082-0.083(Q/235)

(12)

D4=1.146-0.148(L/2 000)

(13)

则，侧向冲击下通过修正系数修正后的跨中动态塑性弯矩与静载截面极限弯矩公式为

Mdm=1.421D3D4Ms

(14)

3.3 拟合公式验证

为验证拟合计算公式的有效性，另取几种不同的工况(见表9)并通过软件得出模拟结果，与拟合公式的计算结果进行对比。

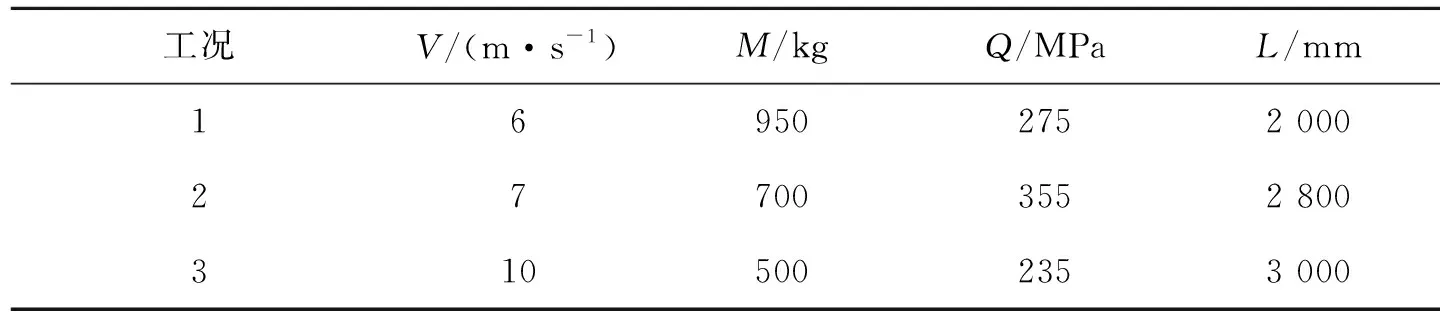
表9 验证工况

通过表10数据的对比分析发现，拟合公式值与软件模拟值相差较小，可用来快速估算冲击荷载下结构的残余变形。

表10 拟合值与模拟值对比

4 结 论

在大量数值模拟结果的基础上，结合刚塑性理论，通过数据拟合，给出了冲击荷载下构件的残余位移简化计算公式，公式值与模拟值误差较小，可用于快速估算撞击荷载下的残余变形。