基于多维尺度法和卡尔曼滤波的机器人传感器网络跟踪定位

严尔军,张 强

(1.青海交通职业技术学院 信息工程学院,西宁 810003; 2.西安理工大学 机械工程学院,西安 710048)

随着人工智能的不断发展,机器人系统已经被广泛应用于各种领域,如分布式传感、目标搜索、采矿、绘制地图等[1-3].无论在任何环境中,必须首先掌握机器人自身以及其在周围环境中的位置关系才可有效地执行任务.在多数场合下,执行任务的机器人数量往往可达数十个之多.目前,对于机器人定位常用的方法是航位推测法,这种方法在近距离定位的情况下精度高,但在长距离运动时误差不断累积,具有发散性,且存在随机误差[4-5],因此,需要绝对定位手段进行校正补偿.GPS作为常用的定位方法,由于其设备太大,无法安装在微型传感器上,GPS不能在室内实现定位,且需要消耗大量的能量.学者们针对GPS定位在室内机器人上的应用开展了大量研究,并提出“到达角”(AOA)技术[6-7],可估计机器人到达信号方向以指出位置,然而这些技术需要天线系统,导致硬件要求非常复杂.同时其缺点是由多径和非视线现象引起的误差[8-9].多维尺度(Multidimensional Scaling,MDS)是指用于多维数据探索性分析的一系列方法.MDS方法最初由Torgerson[10]提出,该算法基于度量分析和余弦定律,将物体放置在欧氏坐标系中,以反映测量的距离或彼此之间的不同.Agrawal等[11]利用MDS算法对由大量节点组成的无线传感器网络进行定位.该方法进行了大量的模拟分析,以解决由各向异性的网络拓扑和复杂地形所造成的缺点,但缺乏对通信成本、消息复杂性和功耗的分析.针对大规模网络中节点距离的传感器功率限制问题,文献[8]提出了用节点间最短路径逼近欧氏距离的MDS-MAP算法,在已知局部连通性的基础上,构造了二维地图,利用Dijkstra算法求出了最短路径,此外,MDS还适用于通过距离测量进行三维定位[12-14].以前,滤波算法是用来减小雷达和生物传感器等跟踪设备造成的测量误差的,然而在距离测量可用的情况下,对跟踪节点的研究还不多见.主要难点在于估计节点间距离的非线性方程.Kalman(KL)滤波器为定位问题构造了一个线性滤波器,MDS定位算法为节点间距离定位提供了有效的模型[15].因此,线性KL滤波器结合MDS跟踪可以将跟踪与独立节点的跟踪扩展到一个考虑节点距离的模型.此外,线性滤波器的有效实现使其适合于更广泛的实际应用.

基于上述原因,本文提出了一个线性卡尔曼滤波器.该滤波器与MDS相结合来跟踪传感器网络节点的位置,给出了一种在测量对应的成对距离时寻找节点变化位置的有效方法,并据此设计了KL滤波器,以实现对室内机器人在传感器网络下的精确定位.

1 定位算法

1.1 MDS算法

经典MDS通常利用相异性矩阵计算低维空间中(通常是二维或三维)对应的节点信息.假设网络中布置有N个需要定位的机器人,每个机器人上设置有传感器网络节点,分别由x1,x2,…,xn表示,D=[dij]N×N为距离矩阵,dij表示节点i与节点j之间的实际距离，即

(1)

式中:m为坐标维度.

MDS方法的目标是在m维空间中找到网络节点[x1,x2,…,xN],xi=[xi1,xi2,…,xim]T使目标函数F(y)最小,得

(2)

式中:yi=[yi1,yi2,…,yim]T为m维空间中的向量.

定义矩阵B=-(1/2)CND2CN,表示X元素的双中心距离平方矩阵,其中CN是中心算子,CN=IN-(1/N)IIT,I是N阶列向量.对矩阵B进行奇异分解(SVD),B=UVUT,获得双中心距离矩阵平方的所有特征向量U和特征值V,进一步可求得N个节点的坐标矩阵为

(3)

由于矩阵B的奇异值求解需要用正交三角(QR)分解来估计所有特征向量和特征值,运算量大,耗时较长.本文利用快速不动点算法来估计B的最大特征向量,将特征向量估计表示为优化问题，即

(4)

在每次迭代时,都采用归一化算法w←w/‖w‖,利用施密特正交化过程,使第p个特征向量与其他特征向量不相关，即

(5)

因此,可获得每个特征向量对应的特征值为

(6)

式(5)和式(6)中提出的增量更新需要多次迭代才能收敛.

1.2 卡尔曼滤波

卡尔曼滤波器根据其测量结果对系统隐含状态进行估计,该滤波器用于处理状态转换和测量过程中出现的高斯噪声.将N个机器人群作为一个离散时间系统，得

(7)

式中:θk为系统在时间指数k时的状态；Zk为Hkθk的测量值和矩阵；Hk为测量结果矩阵，Fk为预测矩阵，其作用是预测下一个取样步骤时的测量值；ωk为过程协方差;vk为测量协方差.

假设wk-1，vk的协方差矩阵Qk和Rk为零均值高斯噪声,则系统状态可以用卡尔曼滤波进行重建，即

(8)

系统状态的更新方程为

(9)

式中:I为单位矩阵;δZk为预测观测值与测量值之间的差值;xk|k-1为系统状态在第k步的先验估计;θk|k-1为系统状态在第k步的先验估计；θk-1为k-1时刻实际测量值；矩阵Fk为预测矩阵，用于预测下一个取样步骤时的测量值；Pk|k-1为状态误差协方差矩阵在第k步的先验估计；Pk为状态误差的协方差矩阵;Kk为卡尔曼增益.

1.3 基于卡尔曼滤波的MDS算法

基于MDS方法获得的传感器网络节点距离定位是非线性的,因此，建立直接模型来反映节点位置的成对距离误差是非常复杂的.在本文中,从给定的测量距离矩阵D中跟踪双中心距离平方矩阵Bk的变化,跟踪系统的状态为矢量，即

(10)

测量矢量Zk是实际距离测量D的双中心距离平方矩阵为

(11)

反映测量误差Zk的噪声模型不再遵循高斯噪声,因此不能使用卡尔曼滤波器.两个传感器节点i和j之间距离测量可表示为

(12)

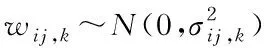
(13)

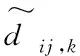
(14)

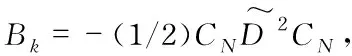
(15)

式中:⊗为Kronecker积,令Λ=CN⊗CN;估计值Zk的协方差矩阵为

E{vect(Bk)vect(Bk)T}=ΛψkΞkψkΛ

(16)

建立了基于MDS跟踪传感器位置的状态方程和测量误差.设系统状态定义为N2×1,xk=vect(Bk)的向量,相应的状态方程可以表示为

(17)

式中:F=IN2.

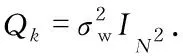
(18)

式中:H为单位矩阵IN2.

vk的协方差矩阵计算式为

(19)

在定义了所有矩阵F,H,Q和R之后,按照式(8)和式(9)方法进行了机器人位置的预测、更新.由于Bk描述的系统状态在每次迭代时都被跟踪,因此,可实时获得矩阵Bk的特征向量和特征值,并根据式(3)获得机器人的位置信息.

2 实验结果

在二维平面内布置N=30个机器人传感器节点的全连通网络用于位置定位,节点最初分布在100 m×100 m的区域内,坐标(10,10),(10,90),(90,10)和(90,90)处固定4个信标用于节点的基准定位.每次迭代获取机器人节点位置时,节点在垂直方向和水平方向上都远离信标,移动步长控制在(0,2)范围内均匀分配.由于噪声随节点间距离的增加而增大,定位估计的精度会随着时间的推移而衰减.为了对比多维尺度法、卡尔曼滤波联合定位方法和其他定位方法的性能,定义第k次迭代处的平均误差距离(MED)为

(20)

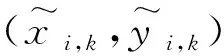
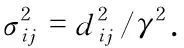
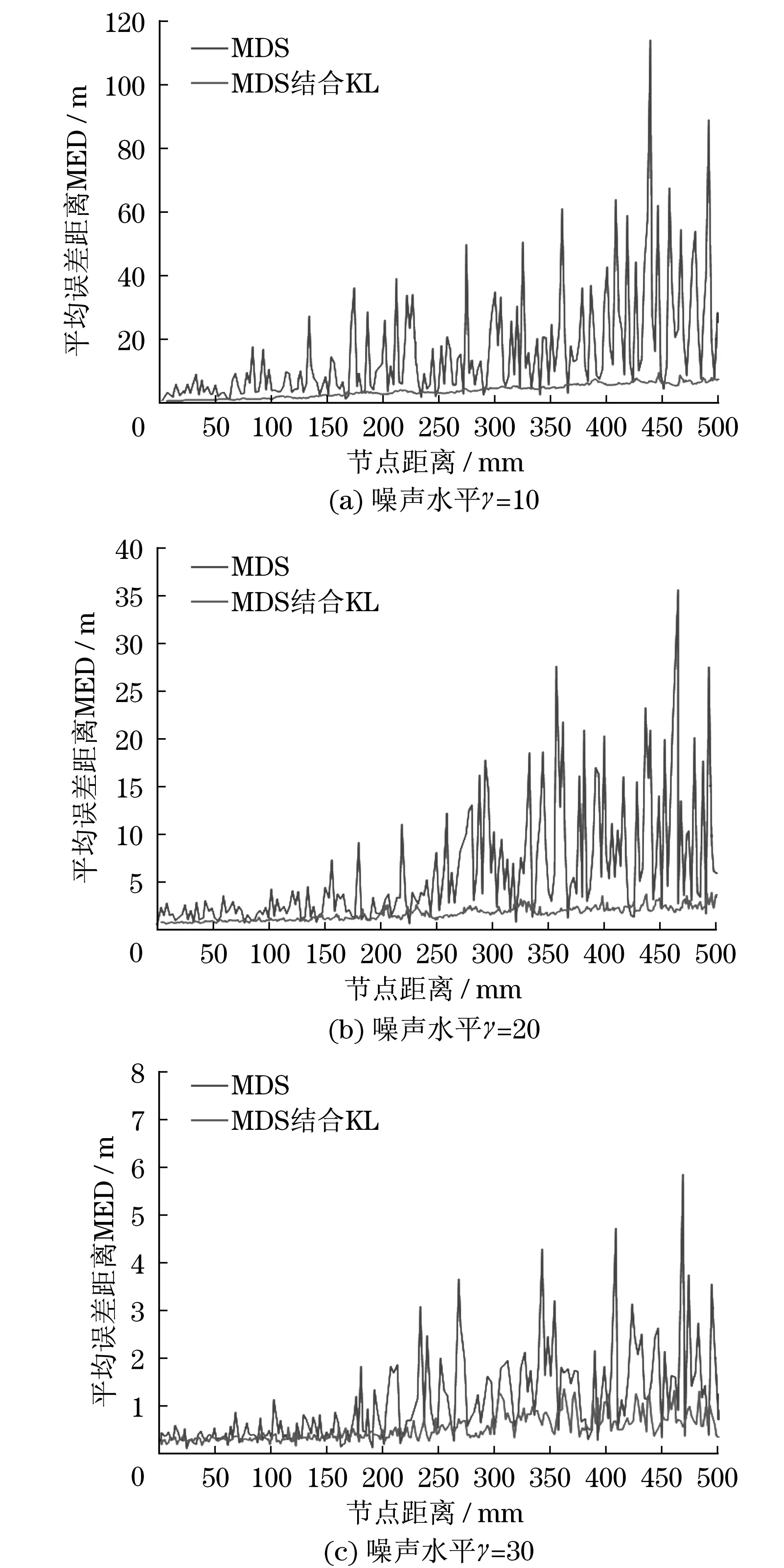
图1 不同噪声水平下的平均误差距离Fig.1 Mean error distance under different noise levels

由图1可知：随着传感器网络节点逐渐远离原点,噪声干扰对距离测量误差的影响逐渐增大.基于MDS法的机器人传感器网络节点定位误差随距离的增大逐渐发散,存在较大误差.而本文提出的MDS和KL联合定位方法测量的平均误差距离MED逐渐收敛,远低于传统的MDS定位方法.在γ=10噪声水平下,MDS法定位误差高达100多m,而本文提出的MDS和KL联合定位误差小于20 m;同样,在γ=20,定位误差小于5 m,在γ=30,定位误差在1 m左右.相比于MDS法,误差减小到20%以下，证明了本文提出的MDS和KL联合定位方法对提高定位跟踪性能的有效性.

在时间为150 s及γ=30噪声水平下,对机器人传感器网络节点位置信息进行了测量,如图2所示.通过显示与原始节点之间的实际位置、估计位置,对MDS结合KL定位方法进行了定性评价.由于噪声的影响,估计的位置与节点的实际坐标间存在较大的距离误差.采用MDS和KL联合定位方法,误差的波动远小于传统的MDS定位方法.

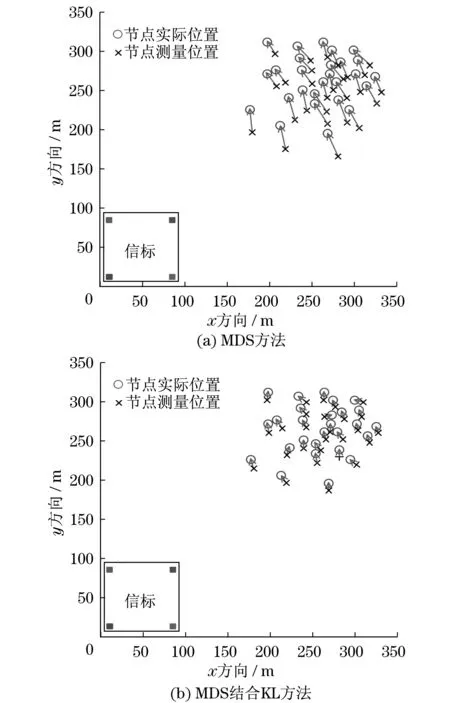
图2 不同定位方法下机器人群位置信息Fig.2 Robots position information under different positioning methods

取其中一节点,获得t=200 s时节点的运动轨迹,如图3所示.在连续时间内,基于MDS的节点移动轨迹呈现出快速变化,而采用MDS结合KL法得到的节点轨迹更为光滑,更适合节点实际运动的估计.

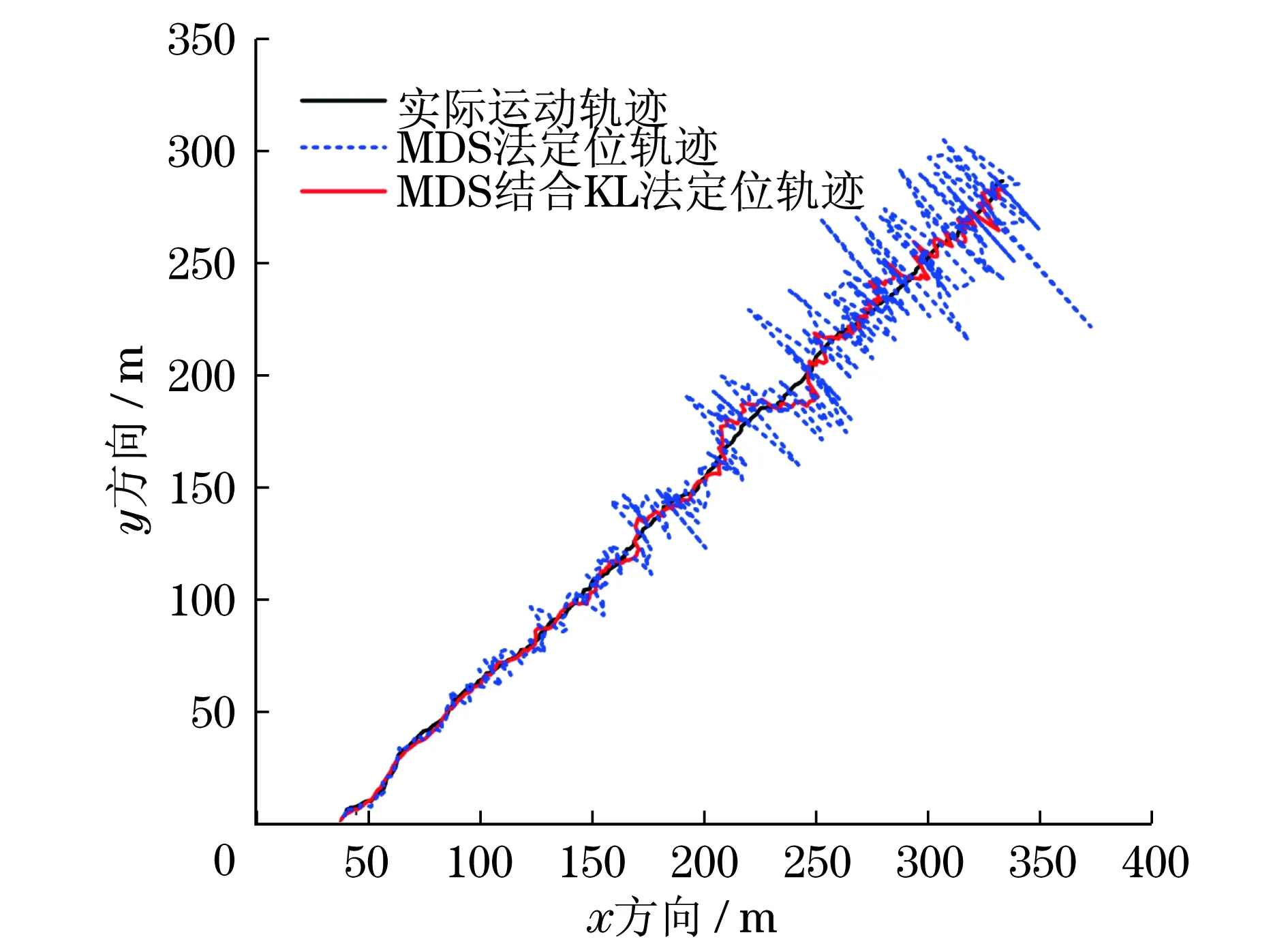
图3 不同定位方法下单个机器人节点运动轨迹Fig.3 Single robot node trajectory under different positioning methods

进一步研究在不同节点数量二维传感器网络下,传统MDS法、扩展卡尔曼滤波方法及MDS和KL联合定位方法的定位性能,机器人节点数量分别为N=20和N=30,测量时间为t=100 s,如图4所示.对比不同定位方法下的误差变化如表1所示.

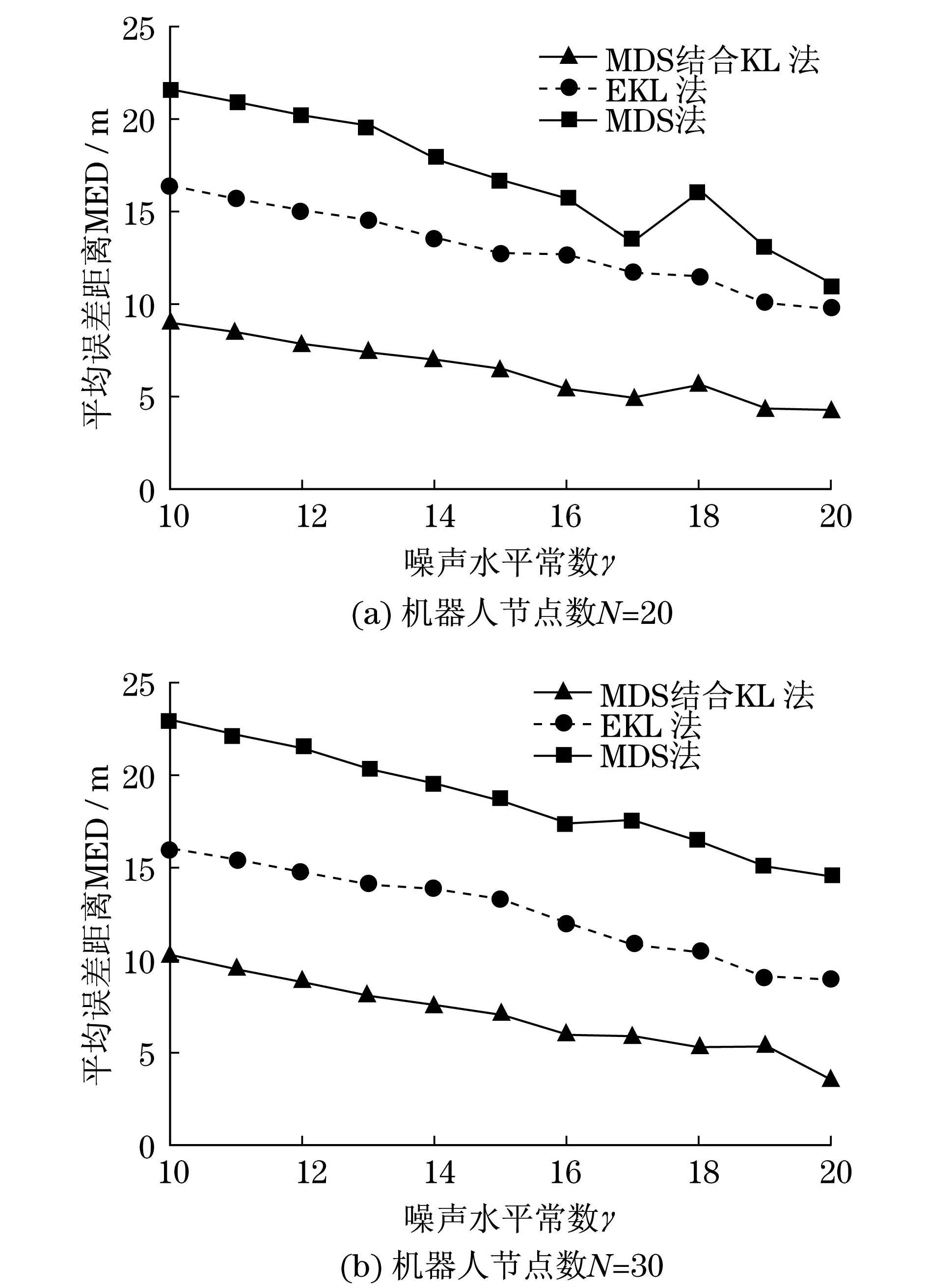
图4 不同节点数量下各定位方法的平均误差距离Fig.4 Mean error distance of different positioning methods under different robot numbers表1 不同定位方法下的误差变化Tab.1 Error under different positioning methods

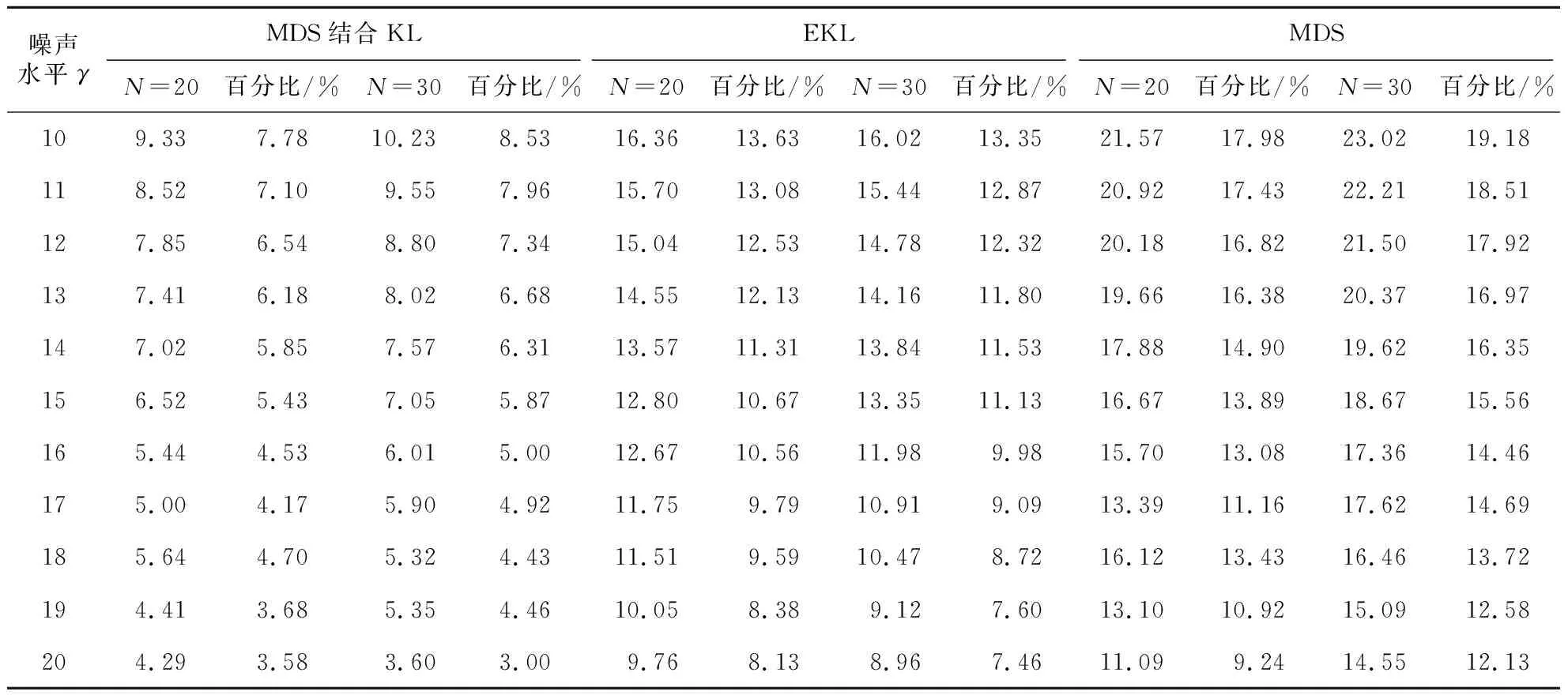
噪声水平γMDS结合KLEKLMDSN=20百分比/%N=30百分比/%N=20百分比/%N=30百分比/%N=20百分比/%N=30百分比/%109.337.7810.238.5316.3613.6316.0213.3521.5717.9823.0219.18118.527.109.557.9615.7013.0815.4412.8720.9217.4322.2118.51127.856.548.807.3415.0412.5314.7812.3220.1816.8221.5017.92137.416.188.026.6814.5512.1314.1611.8019.6616.3820.3716.97147.025.857.576.3113.5711.3113.8411.5317.8814.9019.6216.35156.525.437.055.8712.8010.6713.3511.1316.6713.8918.6715.56165.444.536.015.0012.6710.5611.989.9815.7013.0817.3614.46175.004.175.904.9211.759.7910.919.0913.3911.1617.6214.69185.644.705.324.4311.519.5910.478.7216.1213.4316.4613.72194.413.685.354.4610.058.389.127.6013.1010.9215.0912.58204.293.583.603.009.768.138.967.4611.099.2414.5512.13

分析可知：在不同节点数量和不同噪声水平下,EKL相比传统MDS法在一定程度上降低了节点的定位误差,但与传统MDS和EKL相比,本文提出的MDS结合KL法的传感器网络定位方法显著降低了定位误差.不同噪声水平及不同传感器网络节点数量下,基于MDS法的传感器网络节点定位误差最高接近20%,基于EKL法的定位误差在7.46%～13.13%范围内变化,而本文提出的MDS和KL联合定位方法误差始终控制在8%以内,表明此方法可有效应用于传感器网络下机器人的定位.

3 结语

本文提出了一种基于MDS和KL滤波器相结合的机器人传感器网络节点有效定位跟踪算法.使用4个已知位置的信标,可实现对任意位置处节点的定位.利用MDS提供了所有传感器节点的成对距离矩阵,针对MDS法定位中受到噪声的影响,特别是当传感器节点远离其他传感器节点时,噪声水平会增加,引入KL滤波器有效降低了噪声引起的定位干扰.通过仿真实验验证了该算法的有效性,表明该算法在定位精度上优于传统的MDS和EKL跟踪算法，同时，该算法有效地降低了实际环境中的噪声影响,具有很好解决移动传感器定位问题的潜力,满足了高精度定位的实际要求.