基于退火遗传算法的多连接查询优化应用研究*
2018-12-24赵宇兰
赵宇兰
(山西大学商务学院 信息学院,山西 太原 030031)
0 引言
查询优化是数据库技术的研究重点,而多连接查询(Multi-Join Query,MJQ)是查询优化的一个技术难点。在分布式数据库中,MJQ连接次序的选择是影响查询性能的关键因素,如何寻找多个关系的最佳连接次序,使得查询的执行代价最小,仍然是一个NP-hard问题。本文应用退火遗传算法来解决多连接查询优化问题,通过实验得到一组遗传控制参数的最佳值,并比较了在连接关系个数不同情况下本文算法与基本遗传算法的性能。
1 MJQ问题描述
在传统的关系数据库应用中,单个查询涉及的关系个数N通常比较小(N<10),关系中包含的元组个数也不多。随着现代数据库应用复杂性的需要以及数据量的急剧膨胀,单个查询中包含的Join数也在增加,这为多连接查询的优化增加了难度。
MJQ问题可以采用查询图G=(V,E)描述,其中,R∈V为查询图中所有结点的集合,即基关系集;J∈E为查询图中无向边的集合,即连接操作。
对于一个多连接查询Q=(R1joinR2)AND(R2joinR3)AND(R3joinR4) AND(R4joinR5) AND(R5joinR2),对应的查询图如1所示。
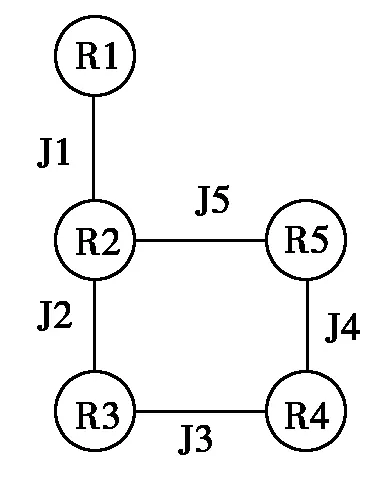
图1 MJQ图
图1的任何一种可能的连接序列可以转化为一种连接树。查询Q的搜索空间为上述5个基关系的所有排列。n个基关系对应的连接树的数目T(n)在不排除笛卡尔积的情况下可以由如下递归形式表示[4]:
(1)
将基关系的连接次序考虑在内,对于n个基关系,则存在T(n)=T(n)n种不同形态的二叉树。一个MJQ对应的所有可能的查询语法树,构成了MJQ的计划搜索空间[5]。
MJQ问题的求解目标就是在计划搜索空间中寻找逻辑等价的执行代价最小的连接树。由于查询处理的代价与中间操作结果的元组数目相关,因此MJQ的执行代价可以用MJQ过程中产生的中间结果的元组数的总和表示。
假设一个连接操作J=R1joinR2,在属性值均匀分布的情况下,计算代价为:
(2)
其中,|R|表示关系R的元组数;C表示R1和R2的公共属性集,ci为R1和R2的某个公共属性;v(s,R)表示R中属性s的不同取值的数目。
(3)
假设多连接查询中包含n个基关系,则每个查询计划的执行代价cost可以通过连接树中所有中间关系Ji的元组数的总和进行估算,估算公式为:
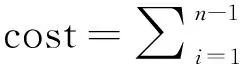
.(4)
MJQ优化的目标是找出查询计划集合C中的一个c0使其满足
cost(c0)≈mincost(c),c∈C.
(5)
2 利用模拟退火算法对遗传算法进行改进
基本遗传算法(Simple Genetic Algorithm,SGA)的形式化定义为8元组:SGA=(C,P0,E,M,Ps,Pc,Pm,T),其中,C为染色体编码方法,P0为初始种群,E为染色体的适应度函数, M为群体规模,Ps为选择算子,Pc为交叉算子,Pm为变异算子,T为算法终止条件[5]。为了避免遗传算法过早收敛,杨艺等在SGA算法中引入了模拟退火机制,形成了退火遗传算法(Simulated Annealing-Genetic Algorithm,SA-GA)。SA-GA算法的主要实现步骤见表1。
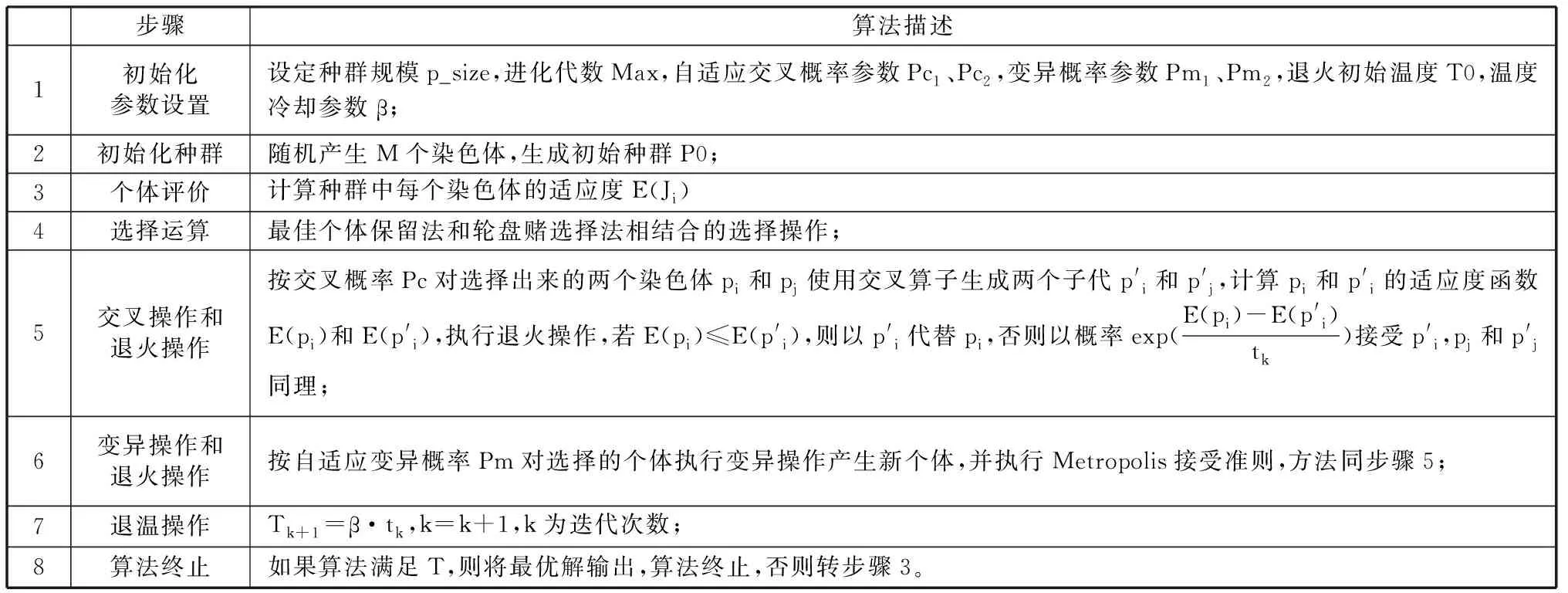
表1 SA-GA算法的实现步骤
3 SA-GA算法在MJQ优化中的应用
3.1 生成有效连接树
假设R为查询图G所有基关系集,J为连接操作序列集合,根据查询图G构造一棵连接树的算法。考虑到连接树生成过程中,没有连接属性的关系存在笛卡儿积,影响算法的效率,因此,加入启发式信息来避免产生无效连接树。
连接树生成算法实现过程如下:
Create_tree()
{计算J中连接操作的个数n
FOR 1 .. n DO
{ LTree=R中包含J的左关系结点;
RTree=R中包含J的右关系结点;
IF LTree<>RTree
以LTree为左子树,RTree为右子树,Ji 为根结点,建立连接子树SubTree;清除R中的LTree和RTree;插入到R中;
END IF
END FOR
END Create_tree
3.2 设计适应度函数
由于连接树的代价越小,其对应的执行计划越优,查询效率越高。本算法依据 (2)(3)(4)式中MJQ代价模型设计适应度函数,其表达式如下:
E(Ji)=(1/cost(Ji)).
(6)
其中,E(Ji)为第J代种群中染色体Ji的适应度函数值。
3.3 生成初始种群
SA-GA算法的演化过程在不断变化的种群中完成,因此初始种群的生成和种群规模会直接影响算法的效率。对于查询图G,生成初始种群的过程如下:
FOR i=1 .. p_size DO
Create_tree();
按照3.1染色体编码规则生成一个染色体;
加入染色体到初始种群p0;
ENDFOR
4 实验设计和结果分析
4.1 实验设计
实验过程分三个步骤进行:
1) 测试初始种群规模对查询计划执行代价值的影响。
2) 算法执行300代,分析历代适应度函数变化趋势,测试算法的收敛性。
3) 对SA-GA和SGA进行对比实验,验证SA-GA算法的有效性。
4.2 实验结果分析
1) 不同初始种群p_size下的SA_GA性能比较
随机生成10个关系,测试不同种群规模下算法执行5次的计划生成代价均值。其他控制参置为:进化代数Max为300,交叉概率Pc1=0.9、Pc2=0.4,变异概率Pm1=0.1、Pm2=0.006,退火初始温度T0=2 000,温度冷却参数β=0.6。运行结果如表2。
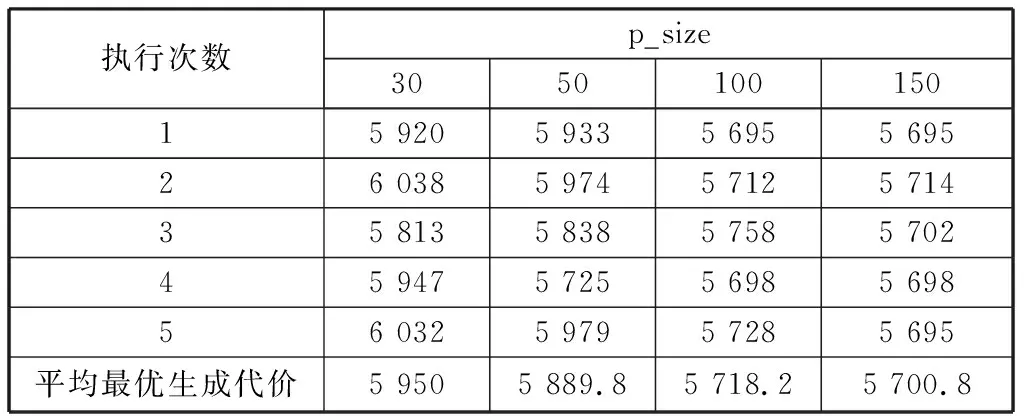
表2 不同种群p_size下的运行结果
从表2数据看出,当p_size=100 时,SA_GA算法的性能要优于p_size=30和p_size=50,并与p_size=150时差别不大,因此p_size=100为较好的选择。
2) 测试历代适应度函数变化趋势
以10个关系的连接操作为例,初始种群规模100,其他参数同1),算法执行5次取均值,经过300代遗传,适应度函数变化趋势如图2。
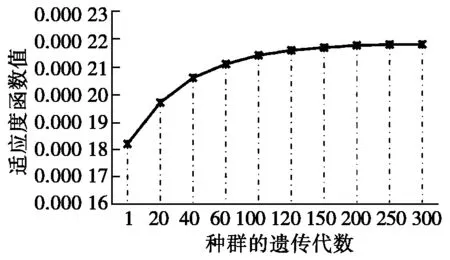
图2 适应度函数变化趋势
从图2可知,算法经过200代遗传后适应度函数值趋于稳定,连续保持最佳100代,执行代价为5 695,计划生成时间为0.785 698秒。实验结果证明算法具有良好的收敛性,可以得到最优解。
3) SA-GA与SGA的对比分析
测试关系个数分别为2~30时,SA-GA和SGA的计划执行代价、计划生成时间和查询响应时间。对于不同关系个数情况下的查询,两种算法各执行10次取平均值。图3是不同关系个数下两种算法计划执行代价对比图。图4是不同关系个数下两种算法的响应时间对比图。图5是不同关系个数下两种算法计划生成时间对比图。
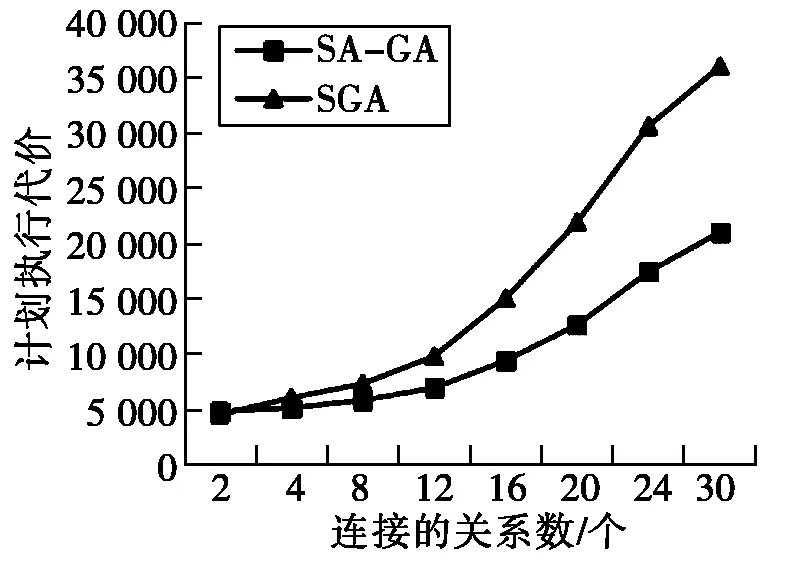
图3 两种算法的计划执行代价对比
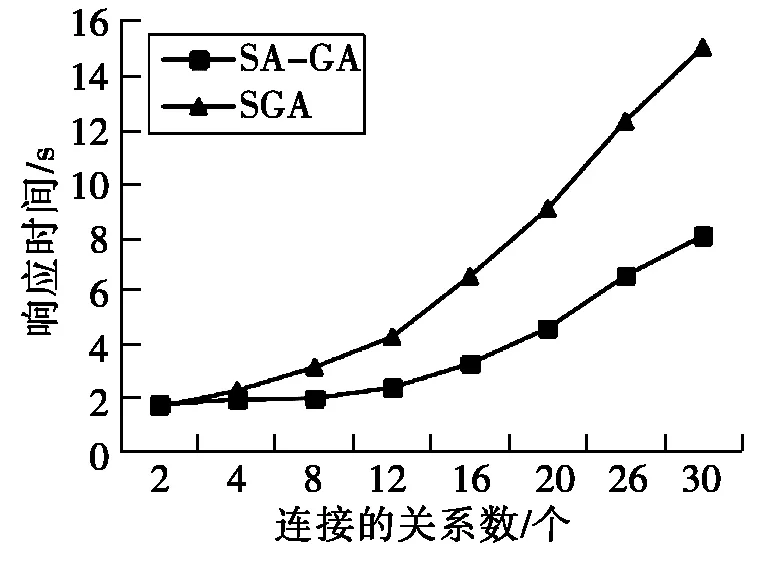
图4 两种算法的查询响应时间对比
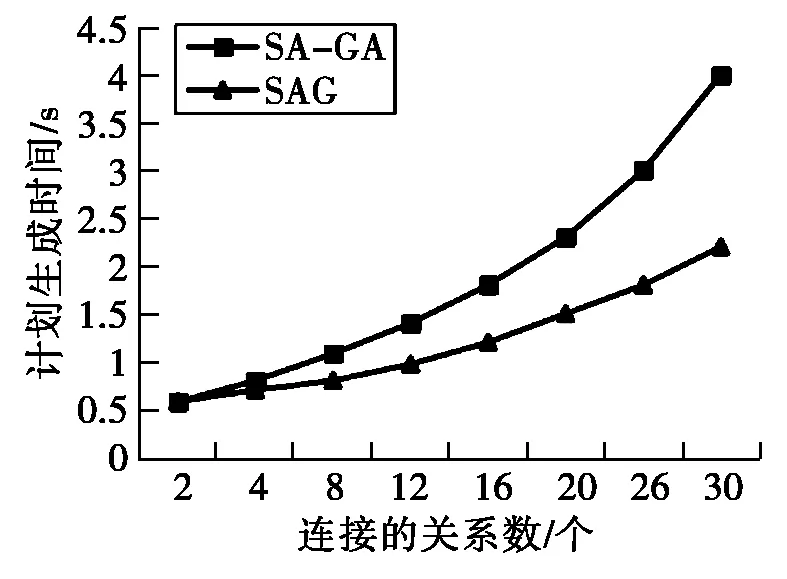
图5 两种算法的计划生成时间对比
实验结果表明,当连接的关系数小于4时,两种算法的计划执行代价和计划生成时间基本相同。但随着连接的关系数的增加,SA-GA算法的查询优化效果明显好于SGA,查询响应时间降低了近50%。这是因为采用自适应交叉和变异概率,增加了种群的多样性,有效地平衡了算法的全局与局部搜索能力,大幅度地降低了计划执行代价。
不足的是,SA-GA算法的计算复杂度要高于SGA算法,因此,计划生成时间要比SGA算法长。但由于SA-GA算法能生成比SGA算法更优的查询执行计划,且执行代价更低,响应时间更短,可以在可接受的计划生成时间内得到近似于最优的计划。
5 总结
针对遗传算法局部搜索能力不强,容易过早收敛的弊端,将模拟退火机制引入到种群的交叉、变异过程中,以期获得全局最优解。仿真实验验证了退火遗传混合算法在MJQ中的有效性。实验结果表明,连接关系数越多,该算法的寻优效果越显著。但是,由于遗传算法本身的局限性,遗传算子的设计以及两种变异的变异率对算法的影响还需要做更多的研究与改进。
