区域极端暴雨非连续性影响频率分析

李 丽

(辽宁抚顺清原满族自治县基层水利管理服务总站，辽宁 抚顺 113015)

当前全球性气候变化对区域水循环的过程产生了一定的影响，主要对区域极端暴雨洪水时间的频率上产生不同程度的影响，对暴雨洪水时空变化规律影响程度较高，同时对当前水利工程防汛应急造成不同程度的威胁[1]。而且，在气候变化影响下，水文极值序列的一致性假设受到极大挑战，非一致性问题给水文极值序列频率分析带来了极大的困难[2]，为此急需对气候变化下的水文非一致性频率影响进行评估，GAMLSS模型主要用于气候变化影响暴雨洪水非一致性评估模型[3- 8]，本文以北方典型干旱半干旱区东白城子流域为研究对象，定量分析区域暴雨洪水极值的变化规律与气候变化扰动之间的关系，从而分析气候变化扰动对区域暴雨洪水极值的影响，研究成果对于气候变化下北方干旱半干旱区的防洪及生态安全影响具有重要参考价值。

1 研究方法

GAMLSS模型在概率密度函数f(yi|θi)认为随机变量yi服从θi=(μi，σi，υi，τi)的概率分布，每个参数都可以表示为解释变量的函数。其中μi，σi分别为位置参数和尺度参数，表示分布的均值和标准差，υi，τi为分布的形状参数，分别表示峰度和偏度。通过单调函数gk(·)，可以表示出分布参数θk与解释变量Xk之间的关系：

(1)

即

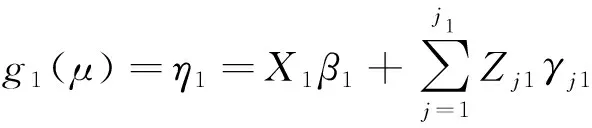
(2)

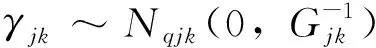
如果不考虑随机观测变量的参数分布影响，则可令jk=0，模型转换方程变为：

gk(θk)=ηk=Xkβk

(3)

若假定随机变量Y服从两参数概率分布，那么GAMLSS模型为：

g1(μ)=X1β1
g2(σ)=X2β2

(4)

模型假定随机分布参数与时间之间的变化矩阵方程为：

(5)

将式(5)带入式(4)，得到分布参数与时间t的函数关系：

g1(μt)=β11+β21t+……+βI11tI1-1
g2(σt)=β12+β22t+……+βI22tI2-1

(6)

GAMLSS模型的回归参数β的似然函数为：

(7)

以物理因子为解释变量，则分布参数与其关系可表示为：

(8)

采用RS算法以似然函数最大为目标函数，求解回归参数β的最优值。

2 研究区域概况

绕阳河为辽河中下游支流，全长283km，整个流域集水面积10360km2，绕阳河流经辽宁阜新、盘锦两个城市，流域平均河道比降为0.26%，区域属于北方典型干旱半干旱区域，近些年来，受到气候扰动变化影响，区域暴雨洪水极端天气较为频繁，暴雨洪水的非一致性频率受到不同程度的影响。

2.1 暴雨极值的非一致性分析

本文所分析的全球气候变化信号为：北极涛动(AO)、北太平洋涛动(NPO)、太平洋年代际振荡(PDO)与南方涛动(SOI)。多项研究表明上述4种气候变化信号对中国区域气候有显著影响。利用GAMLSS模型构建分布参数与解释变量的统计关系(本文为时间(ti)、气候指标)。当累计概率分布参数为常量时，GAMLSS模型就变成传统的一致性模型(M0);当模型中累计概率分布参数随时间ti变化时，GAMLSS模型为非一致性模型(M1)；当累计概率分布参数随气候指标变化时，GAMLSS模型为非一致性模型(M2)。本文对三种模型分别进行分析，见表1。利用AIC准则来优选模型(Model1、Model2、Model3)，AIC越小，模型越好，见表2。

对于三个模型，AIC值最小的分布均为对数正态分布(LOGNO)，其中最小的为考虑气候指标的Model 3，统计参数时变模型Model 2与一致性模型Model 1模拟效果相近。

表1 气候扰动非一致性模型描述

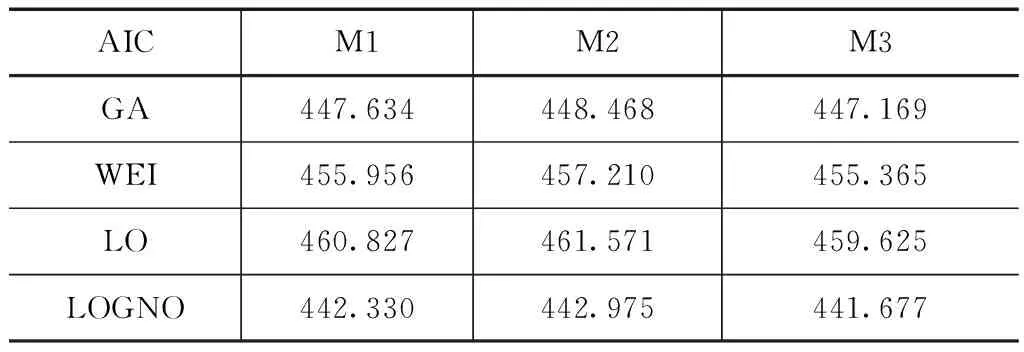
表2 各模型年最大降雨量序列模拟AIC值

2.2 气候扰动变化区域暴雨极值的非一致性评估

结合后不同模型构建了评估方程，基于各评估方程对各气候扰动模式下暴雨极值的非一致性进行评估，评估结果见表3—4，各模型年最大降雨量序列拟合残差worm图和Q-Q图如图1所示。

表3 各模型年暴雨极值序列模拟参数值

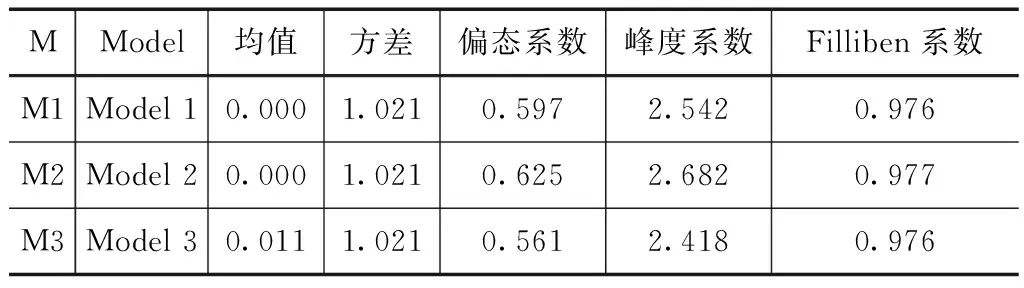
表4 各模型拟合残差的分布矩及计算的Filliben系数

各模型年最大降雨量序列最优分布的参数(μ和σ)见表3，一致模型(Model 1)的μ和σ均为常数；时变模型(Model 2)的μ是时间t的线性函数，σ为常数；利用R平台“gamlss”包里的逐步回归方法(stepwise)，通过优选，考虑气候指标模型(Model 3)的μ为一个常数，σ与气候指标PDO成线性关系。表明东白城子流域年最大降雨量均值比较稳定，其波动主要是受太平洋年代际震荡PDO所影响。表4给出了各模型年最大降雨量序列GAMLSS模型拟合残差的分布矩及Filliben系数，从表4中可以看出，Filliben系数均较高，表明模型模拟效果较好。

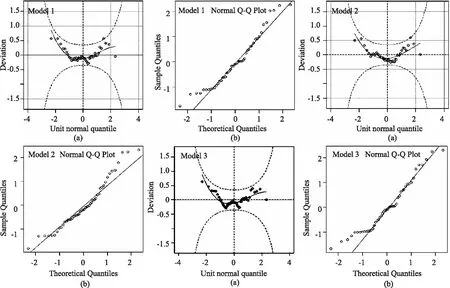
图1 各模型年最大降雨量序列拟合残差worm图(a)和Q-Q图(b)

M1、M2和M3的三条分位数曲线如图1所示，对应频率分别是2.5%、50%和97.5%。可以看出，对于一致性模型(M1)，给定频率下的年最大降雨量值始终为一个常数，无法识别出年最大流量的变化趋势。对于非一致性模型M2，其分布参数是时间的线性函数，蓝色线识别出东白城子流域的年最大降雨量呈上升趋势，这与前文的MK检验结果一致，这表明分布参数时变的非一致性模型M2具有能有效识别序列变化趋势的能力。然而，M2只能识别出整体的变化趋势，在各个时段内的变化无法判断，如年最大降雨量在2002年后呈现轻微的下降趋势。

3 结论

(1)东白城子流域年最大降雨量序列在M1、M2和M3条件下的最优分布均为对数正态分布(LOGNO)，M1的均值μ和方差σ为常数，M2的μ与时间呈线性关系，σ为常数，M3的μ为常数，σ与PDO呈线性关系。东白城子站和韩家杖子站年最大流量序列在M1、M2和M3条件下的最优分布均为对数正态分布(LOGNO)，M1的均值μ和方差σ为常数，M2的μ与时间呈线性关系，σ为常数，M3的μ与AO呈线性关系，东白城子站的σ为常数，韩家杖子站的σ与AO呈线性关系；

(2)东白城子流域年最大降雨量序列和东白城子站及韩家杖子站的年最大流量序列的非一致性模型(Model 2和Model 3)的AIC值均比一致性模型(Model 1)要小，即非一致性模型能更好地描述年气候变化扰动下北方旱区的暴雨极值的非一致性。