磁场的环量:从含时场到稳恒场
2018-12-24李凤敏
李凤敏
(天津职业技术师范大学理学院 天津 300222)
磁场的环量是描述磁场的一个重要物理量.对于静磁场或者恒定磁场,磁场的环量由安培环路定理给出,其形式是[1,2]
∮B·dl=μ0Ic
(1)
方程左边环路积分中的磁感应强度来自于电路中各处电流的贡献.方程右边的电流是穿过环路的传导电流
(2)
对于稳恒情况,电路或者电流是闭合的,电路中的任意地方传导电流都是相等的.对于开放电路,例如一段在空间运动的带电直线等,电磁场是随时间变化的,磁场的环量由全电路的安培环路定理给出
(3)
方程右边括号中的第二项是位移电流,是电位移通量的时间变化率.如果带电直线段变成无限长,那么电场磁场都不随时间变化了,教科书中一般会这样解释:此时位移电流消失,全电路的安培环路定理式(3)就变成了稳恒电路的安培环路定理式(1).但是,位移电流是怎么慢慢消失的,一般没有说明详细的过程.为了研究清楚其中的细节,有必要从非稳恒情况,例如一段运动的有限长的带电直线出发,考察从式(3)到式(1)的详细过程.
1 从非稳态到稳态
如图1所示,假设电流沿z轴从负的无限远处向正的无限远处流动,闭合环路设在原点O处.下面分3种情况讨论全电路的安培环路定理:(1)电流到达P1点;(2)电流到达P2点;(3)电流到达无限远处.

图1 电流沿z轴从负的无限远处向正的无限远处流动
1.1 当电流到达P1点
当电流到达P1点时,传导电流没有穿过环路,因此式(3)为

(4)
如图2所示,在P1(0,0,z)点处取电荷dq(记dq=Q),其在圆平面上场点(x,y,0)的场强
(5)

图2 电流到达P1点
该场对以O为圆心,以R为半径的闭合回路所围圆面的电位移通量为
积分得

(6)
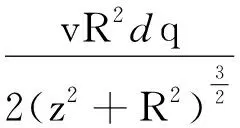
(7)
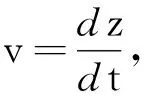
从负无穷到P1点的所有运动电荷对该环路的位移电流为
(8)
此时由全电路安培环路定理及位移电流可计算环路上任意点的磁感应强度的大小,根据式(4)及式(8)有2πRB=μ0ID,即
(9)
如图3所示,利用任意一段载流直导线的磁场公式
(10)
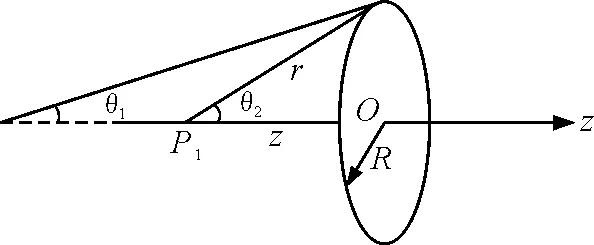
图3 一段载流直导线的磁场
结果与式(9)完全相同,也就是说环路处的磁场完全由运动电荷产生,而位移电流对磁场的贡献为零,这一结论与相关文献[3~6]的观点一致.
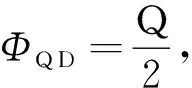
IQD+Ic=0
(11)
1.2 当电流到达P2点
接下来分析电流穿过如图1所示的回路到达P2点的情况.当电流到达P2处时,Q的电场对圆环平面的电位移通量

(12)
位移电流为

(13)
由于电流到达P2处时有传导电流穿过环路,因此
∮B·dl=μ0Ic+IQD+ILD+IRD
(14)
式中IQD,ILD,IRD分别代表正在通过回路、回路左边和回路右边的电荷对位移电流的贡献.下面分别对ILD,IRD进行计算.
回路左边的电荷对位移电流的贡献可由式(7)积分得
(15)
回路右边的电荷对位移电流的贡献由式(13)积分得
(16)
将式(11)、(15)、(16)代入式(14)中得2πRB=μ0ILD+IRD,即
(17)
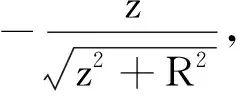
此结果与式(17)完全相同,再次看到环路处的磁场完全由运动电荷即传导电流产生,位移电流对磁场的贡献为零.

图4 电流到达P2处
1.3 当电流到达无限远处
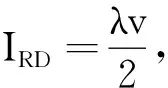
无限远,电流稳定后由式(14)、(15)、(16)有
∮B·dl=μ0λv=μ0Ic
(18)
式(18)即为稳恒电流的安培环路定理,其中的传导电流是电路中各处位移电流之和.由此我们知道安培环路定理两边的来源也是一致的.
2 结束语
从一段运动的带电直线形成的开放电路出发,通过微观层次上的电荷运动,讨论了从全电路的安培环路定理到恒定情况下安培环路定理的详细过程.从全电路的安培环路定理回到恒定磁场安培环路定理的关键是,对于恒定情况,全电路中各处运动电荷的位移电流之和数值上正好等于传导电流.希望这一结果对于更好地理解安培环路定理有所帮助.
