一些奇异实积分的特殊复围道积分计算方法*

邢家省，杨义川

(1.北京航空航天大学数学与系统科学学院，北京 100191；2.北京航空航天大学数学、信息与行为教育部重点实验室，北京 100191)

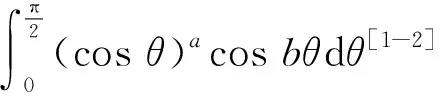
定理1[1-2]设b>a>-1，则

证明设z=eiθ，则

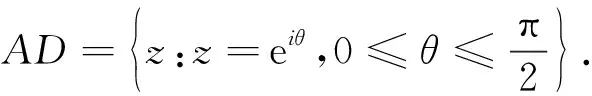
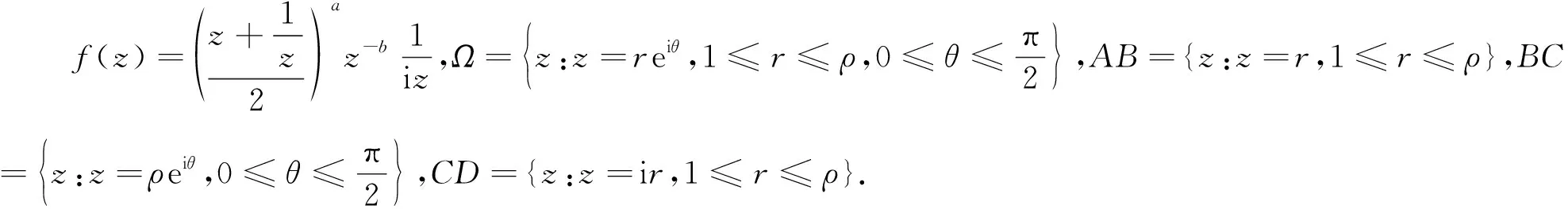
利用贝塔函数与Γ函数的关系[1-2]，可得

于是

从而

利用余元公式[1-2]，可得

对于Γ函数在负的自变量处的定义，是通过余元公式的形式给出的.

定理2[1-2]设-1

设ρ>ε>0，Cε={z:|z|=ε}，Cρ={z:|z|=ρ}，AB={z:z=x,ε≤x≤ρ}.考虑沿道路AB,Cρ,BA,Cε上的复积分，利用留数定理可得

易知

故

(1)

定理3[1-4]设-π<λ<π，则

(2)

定理4[1-4]设0<λ<π，则

由定理3的证明即可给出定理4的证明.

定理5[1-4]设0

定理6[1-4]设0