k级近似概念及其应用

范 妍，魏 玲

(西北大学 数学学院, 陕西 西安 710127)

形式概念分析是由德国数学家Wille于1982年提出的[1]用于数据分析和知识发现的理论。国内外许多学者对形式概念分析进行了深入的研究,并在概念格的属性约简[2-6]、规则提取[7-8]、概念格构造[8-11]等方面取得了一定的成果。形式概念分析已广泛应用于软件工程[12]、决策分析[13]等领域。

在形式概念的数据基础—形式背景上,根据对象拥有的属性是否相同,可将对象集进行划分,从而形成多个对象等价类。魏玲[14]等人通过研究对象等价类与概念的关系,证明了概念的外延一定是由若干个对象等价类的并得到的,而并非等价类的并一定是概念的外延,于是这些不是外延的对象子集涵盖着的有用的信息就不能通过概念来获取。其原因是概念对于对象集和属性集的要求比较苛刻,通过概念来进行形式背景的信息获取有一定的局限性。于是很多学者将获取概念的条件弱化后提出近似概念[8,11,15],从而进一步获取信息。

Wan和Wei在文献[15]中提出基于k-阶关系的近似概念,对某些不是概念却有一定实际意义的二元对进行获取,并且赋予较为其合理的语义解释。本文提出的k级近似概念则是对这种基于k-阶关系的近似概念进行改进,使其具有更符合实际应用的语义。首先,本文研究了k级近似概念的相关性质,及其与形式概念、基于k-阶关系的近似概念之间的关系。此外,本文利用k级近似概念为某些非外延等价类的并赋予合理的语义解释,并据此语义对对象等价类进行排序,最终为实际决策提供帮助。

1 预备知识

1.1 形式概念分析基础知识

定义1[1-2]称(G,M,I)为一个形式背景,其中G={g1,…,gn}为对象集,每个称为一个对象,M={m1,…,mq}为属性集,每个mj(j≤q)称为一个属性,I为G与M之间的二元关系,I⊆G×M。若(g,m)∈I,则g具有属性m,记为gIm。

对于形式背景(G,M,I),在对象子集X⊆G和属性子集B⊆M上可以定义一对对偶算子:

X*={m∈M|∀g∈X,gIm}

B*={g∈G|∀m∈B,gIm}

X*表示X中所有对象共同拥有的属性集合,B*表示共同拥有B中所有属性的对象集合。

本文记{g}*为g*,g∈G;记{m}*为m*,m∈M。若∀g∈G,m∈M,都有g*≠∅,g*≠M,m*≠∅,m*≠G,则称形式背景是正则的。本文研究的形式背景都是正则的,且是有限的。

定义2[2]设(G,M,I)为一个形式背景,X⊆G,B⊆M,如果二元组(X,B)满足X*=B,B*=X,则称(X,B)为一个形式概念,简称概念。其中称X为概念的外延, 称B为概念的内涵。

∀g∈G,(g**,g*)是概念,称其为对象概念。类似地,∀m∈M,(m*,m**)也是概念,称其为属性概念。

文献[2]给出了形式背景下算子的相关性质。

性质1[2]对于形式背景(G,M,I),设X1,X2,X⊆G,B1,B2,B⊆M,则有下列基本性质:

(ii)X⊆X**,B⊆B**，

(iii)X*=X***,B*=B***，

(iv)X⊆B*⟺B⊆X*，

(vii)(X**,X*)和(B*,B**)都是概念。

用L(G,M,I)表示形式背景(G,M,I)的全体概念。若在L(G,M,I)上定义偏序关系为:

(X1,B1)≤(X2,B2)⟺X1⊆X2(⟺B2⊆B1)

若(X1,B1),(X2,B2)∈L(G,M,I),有

(X1,B1)∧(X2,B2)=(X1∩X2,(B1∪B2)**)，

(X1,B1)∨(X2,B2)=((X1∪X2)**,B1∩B2)

也是概念,从而L(G,M,I)是格,并且是完备格,称其为概念格。

∀X⊆G,B⊆M,记IB=I∩(G×B),则有X*B={m∈B|∀g∈X,(g,m)∈I}。当B为属性全集M时,简记为X*。

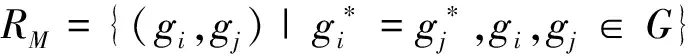
定理2[14]设(G,M,I)为一个形式背景,G/RM为其上的划分,记

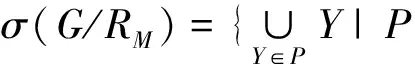
则∀(X,B)∈L(G,M,I),都成立X∈σ(G/RM)。

定理2表明,在形式背景(G,M,I)下,任何一个概念的外延都是由RM中某些等价类的并构成,但等价类的并不一定都是外延。σ(G/RM),若Y**≠Y*,则称Y为非外延类。

1.2 基于k-阶关系的近似概念基本理论

定义3[15]设(G,M,I)为形式背景,∀B⊆M,若

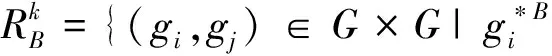
定义4[15]设(G,M,I)为形式背景,∀g∈G,称([g]k-,g*)是g的k-左邻域近似概念,([g]k+,g*)是g的k-右邻域近似概念,分别记为gk-LNAC和gk-RNAC。

定理3[15]设(G,M,I)为形式背景,∀g∈G,有[g](|M|-2)+=g**。

定理3表明,当k=|M|-2时,相应的右邻域近似概念([g](|M|-2)+,g*)是概念格的对象概念。

例1我们将文献15中例1的形式背景进行净化,得到本例形式背景表1。这是一个购房者对于若干小区各项指标是否满意的调查表。其中,G={1,2,3,4,5} 是小区的集合,M={a,b,c,d,e}是调查指标的集合,其中a-房屋价格,b-交通状况,c-娱乐设施,d-物业管理,e-工程质量。在表1中,×表示购买者对此项满意,空格则表示购买者不满意。

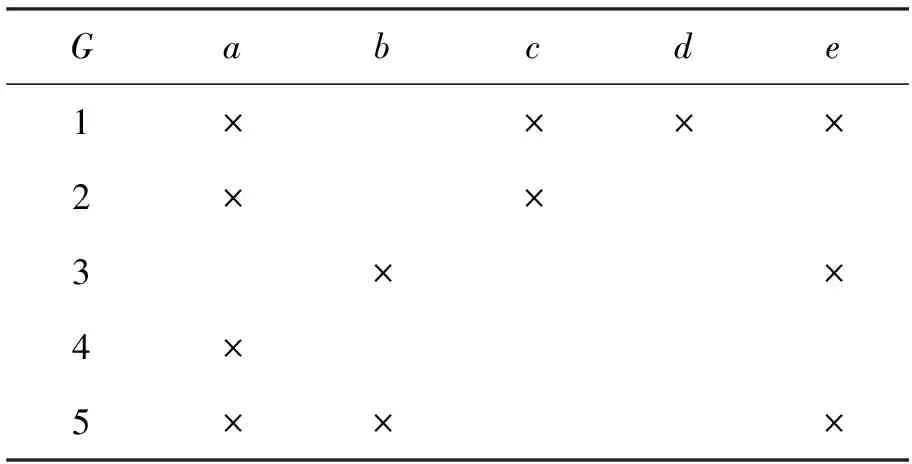
表1 形式背景(G, M,I)Tab.1 A formal context (G, M,I)

为了便于描述,本文例子中的集合均以元素序列形式给出。若取B=M={a,b,c,d,e}则根据定义3和定义4可以得到所有的gk-LNAC和gk-RNAC,如表2和3所示。

我们以对象5为例给出gk-LNAC和gk-RNAC的解释。g0-LNAC=(5,abe):购房者对5号楼盘的房屋价格,交通情况和工程质量均满意。gk-RNAC=(5,abe)(0≤k≤3):能够让购房者在这三方面满意的只有5号楼盘;g1-LNAC=(35,abe):若对房屋价格要求不高,3号楼盘可作为备选;g2-LNAC=(345,abe):若购房者不考虑交通状况和娱乐设施,则还可以将4号楼盘作为备选;g3-LNAC=(345,abe):在不考虑房屋价格、交通情况和工程质量这3个指标时,{3,4,5}是最大的选择范围。

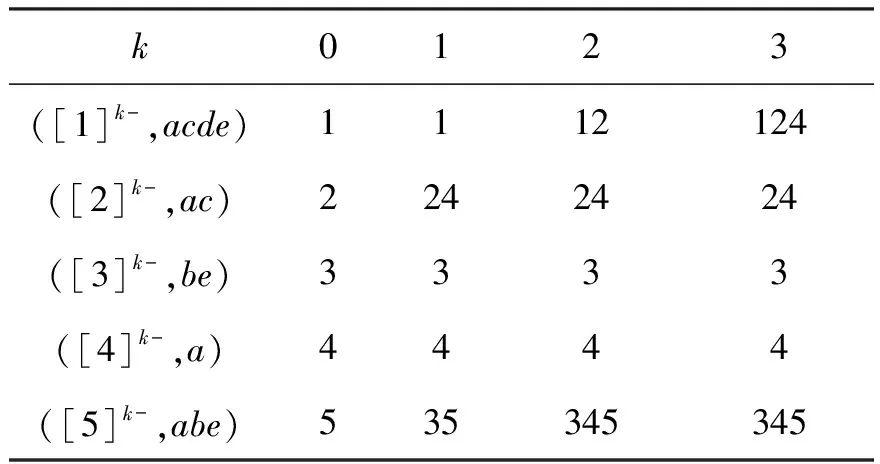
表2 gk-LNACTab.2 gk-LNAC

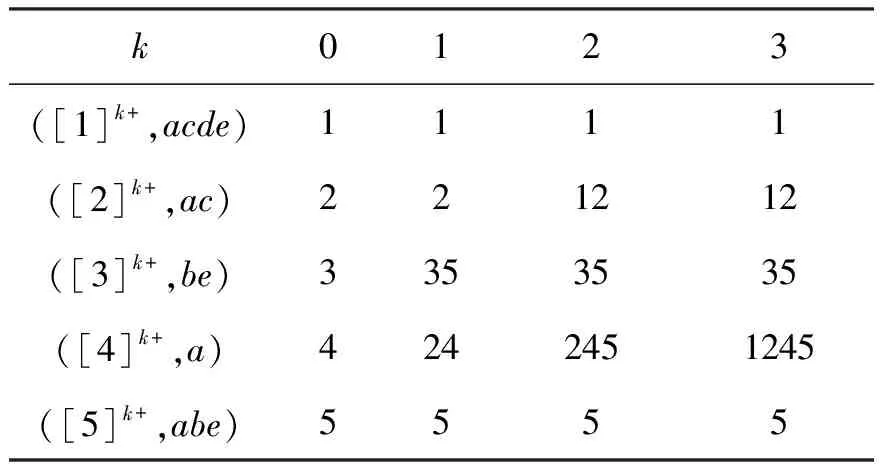
表3 gk-RNACTab.3 gk-RNAC

2 k级近似概念

针对以上分析,本节在k-阶关系基础上提出k级关系,进一步定义k级近似概念,并为非外延类赋予更有助实际决策的语义解释。

2.1 k级近似概念的定义及性质

例2(续例1) 令B=M={a,b,c,d,e},0≤k≤3,我们可以得到每一个对象关于B的k级近似概念，如表4所示。

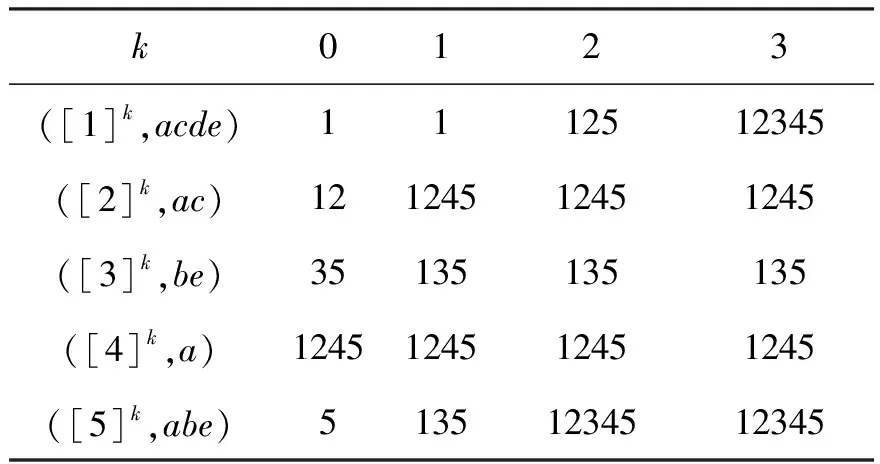
表4 gk-NACTab.4 gk-NAC

以对象5为例来说明k级近似概念对非外延类赋予的语义解释, 若某人对5号楼盘满意:① 0-NAC:(5,abe)表示购买者对5号楼盘的房屋价格,交通情况和工程质量均满意,并且只有5号楼盘能够让购买者在这3个方面满意;② 1-NAC:(135,abe)表示,若购买者愿意放松一个条件以增多备选项,那么放松交通状况的要求,1,5将作为备选,若放松房屋价格的要求,3,5 将作为备选;③ 2-NAC:(12345,abe)表示,若购买者愿意放弃交通情况和工程质量两个条件,那么2和4进入备选范围,1,2,4,5将作为备选;同时,5的2级近似概念表示在只剩一个条件要求时,所有的楼盘均可作为备选。

根据定义5, 可以得出k级近似概念的以下性质。

性质2设(G,M,I)为形式背景,B⊆M,∀g,gi,gj∈G,0≤k≤|B|-1,有

(i) 若k1≤k2,则Rk1(B)⊆Rk2(B);

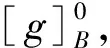
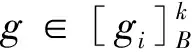
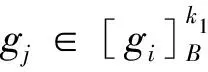
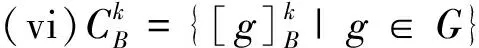
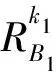
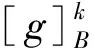
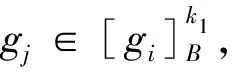
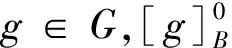
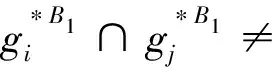
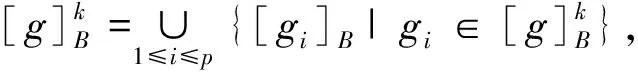
证明根据性质2的(iv)及定义5可证。

推论1和性质2的(iii)将G上的等价关系和k级关系联系起来。

2.2 k级近似概念与形式概念的关系

Düntsch和Gediga在文献[9]中将模态逻辑中的可能性算子与必然性算子引入形式概念分析理论,提出了面向属性概念格;进而Yao又提出了面向对象概念格[16]。随后,这两者的相关研究也已成为形式概念分析理论的重要研究内容之一。本节,我们也考虑这两种算子,并研究相应的概念与k级近似概念的关系。以下的定理4、推论2及推论3给出相关结论。

定义6[9]设(G,M,I)为形式背景,X⊆G,B⊆M,定义□算子和算子:X□={m∈M|m*⊆X},B□={g∈G|g*⊆B},X={m∈M|m*∩X≠∅},B={g∈G|g*∩B≠∅}。

其中,X□表示的属性集合是:具有其中属性的对象一定在X中;X表示的属性集合则是:具有其中属性的对象一定与X有交集。对偶地,B□表示拥有的属性包含在B中的对象集合;B则表示拥有的属性与B交不为空的对象集合。

定理4设(G,M,I)为形式背景,B⊆M,g∈G,则g*B=G⟺[g]|B|-1=G。

证明g*B=G⟺∀gi∈G,都有∅,且⟺G⊆(根据定义5) ⟺

该定理说明, 如果一个对象和其余任意的对象都有共有属性, 那么该对象能与任意对象构成k级关系。

推论2设(G,M,I)为形式背景,∀g∈G,([g]0,g*)是形式背景(G,M,I)的对象概念。

推论3设(G,M,I)为形式背景, (X,B)∈L(G,M,I),则∀g∈X, 存在k使得([g]k,g*)满足B⊆g*,X⊆[g]k。

推论3说明,任一概念的内涵和外延分别包含于某对象的k级近似概念的外延和内涵,而且可能包含于不同对象的k级近似概念的内涵与外延中。

2.3 k级近似概念与基于k-阶关系的近似概念的关系

从本质上,k级关系是对k-阶关系的弱化,从而使得在基于k-阶关系的近似概念的基础上,k级近似概念的对象增多。定理5给出k级近似概念与基于k-阶关系的近似概念的关系。

定理5设(G,M,I)为形式背景,∀g∈G,([g]k+,g*)是g的k-阶右邻域近似概念,([g]k-,g*)是g的k-阶左邻域近似概念,([g]k,g*)是g的k级近似概念,则有

(i) [g]0=[g](|M|-2)+;

(ii)[g]k-⊆[g]k,k≤|M|-2。

证明(i) 根据定理3及推论2可证得。

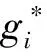
例3(续例2)G={1,2,3,4,5}, ∀g∈G,([g]k+,g*)是g的k-阶右邻域近似概念,根据定理5,有以下结论:

(i)[g]0=[g]3+,表5给出具体结果。即g0能够表示出让购买者在g*这几个方面满意的所有选择;如[5]0=[5]3+,则能够让购买者在房屋价格, 交通情况和工程质量这3个方面均满意的楼盘只有5号楼盘一个。于是,对于购房者在g*的条件下放松0个条件这一情况,([g]k+,g*)在k≤|M|时的取值都是多余的,而([g]0,g*)的表示更为简洁明了。

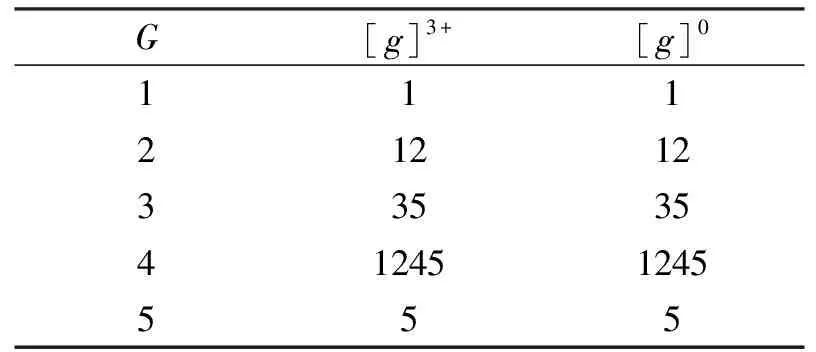
表5 [g]3+与[g]0Tab.5 [g]3+ and [g]0

(ii)[g]k-⊆[g]k,k≤3,表6给出具体结果。于是,对于购房者在g*的条件下放松k(1≤k)个条件这一情况,相比于([g]k-,g*),([g]k,g*)会提供更多的选择。如在2*={a,b}(房屋价格和娱乐设施)两个条件上放松1个条件时,相比于[2]1-={2,4},[2]1={1,2,4,5}会多提供选择1和5,即在不考虑娱乐设施时,1号和5号楼盘也可以作为备选。

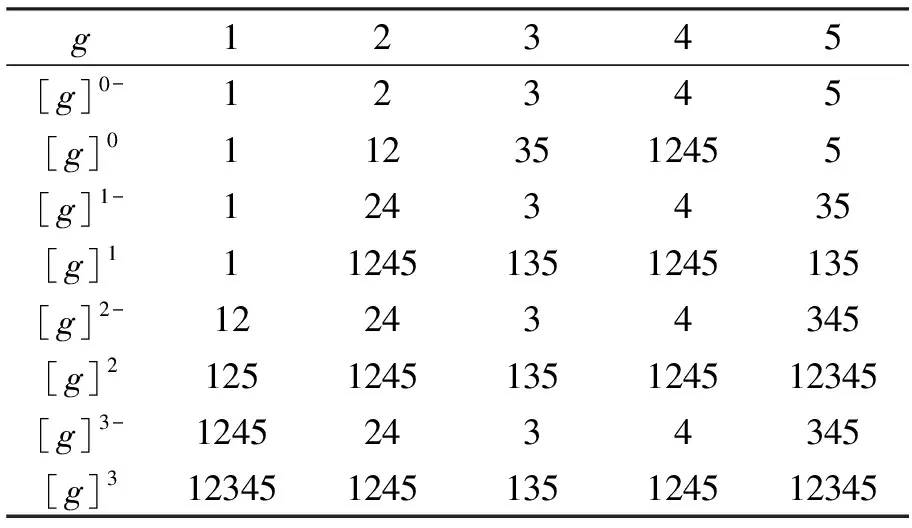
表6 [g]k-与[g]kTab.6 [g]k- and [g]k

应用k级近似概念的语义解决购房推荐这一问题,而这种思想可以进一步拓展到更复杂的推荐工作中。

3 基于k级近似概念的等价类排序

k级近似概念为某些非外延等价类赋予了合理的语义解释,从而给出了所有符合实际要求的决策,并且对基于k-阶关系的近似概念的语义解释做了进一步补充。而实际情况下,满足购买者意愿的往往不只一个,但购买者只能选其一;或购买者无法顾及所有选择,从而有可能错失更为符合自己意愿的选择。此时,我们就需要根据购买者的选择,估测购买者的意愿,进而提供一种针对所有选项的推荐。

本节将对象g的k级近似概念推广到任意对象子集的ki级近似概念,并将其一种语义解释应用于等价类排序。为了研究方便,取B=M。

设(G,M,I)为形式背景,X⊆G为某人满意的对象集,G={g1,…,gn},∀gi,gj∈G,记gj第一次出现在[gi]k中时,k的取值为

kij=

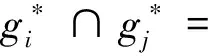
其含义为:若D(X,gk)≤D(X,gj),则gk相对gj更接近X。则有以下结论成立。

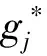
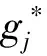
该定理说明,如果一个对象拥有的属性包含另一对象拥有的属性,前者更接近于满意的对象集。

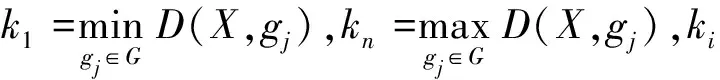
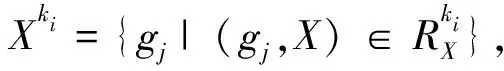
下面给例子说明X的ki级近似概念的语义解释。

例4(续例3) 若购买者对于2和5号楼盘感兴趣,即X={2,5},X={a,b,c,e}。表7给出D(X,gj)的确定,表8是X的ki级邻域。

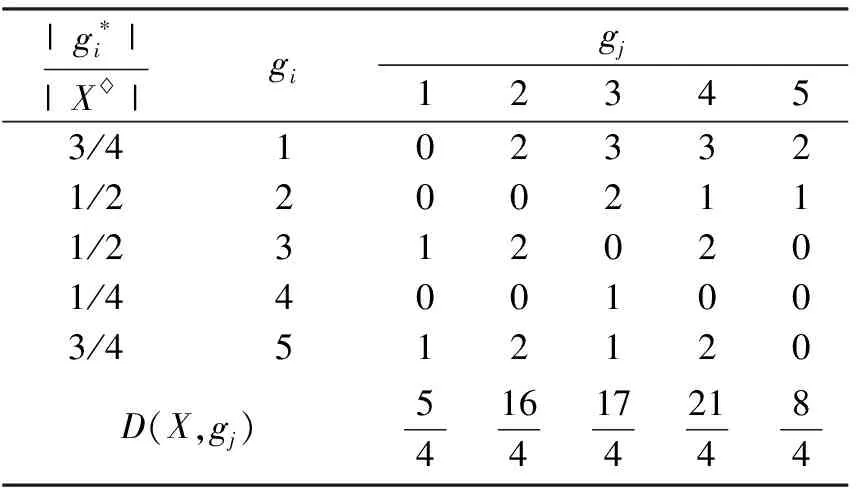
表7 D(X,gj)Tab.7 D(X,gj)

则ki的取值分别为:k1=5/4,k2=8/4,k3=16/4,k4=17/4,k5=21/4。

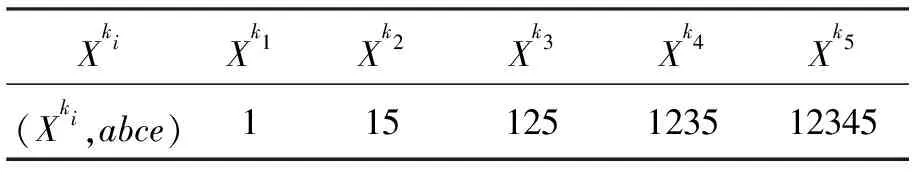
表8 X的ki级邻域Tab.8 Grade kineighborhood of X

X的ki级近似概念的语义解释为:针对购买者的喜好:房屋价格、交通状况、娱乐设施、工程质量,楼盘1为最符合购买者意愿,其次为5号楼盘,2号楼盘,3号楼盘,最后是4号楼盘。

由于X的ki级近似概念基本思想来源于k级近似概念,因此在这里也将其称为k级近似概念。

推荐结果如上,k级近似概念的语义及其应用有以下3个优点:①相比于基于k-阶关系的近似概念的语义解释,k级近似概念的语义扩大了选择范围;②适用于购买者有不只一个满意对象时的推荐工作;③当购房者没有办法顾及所有选择的情况下,给出更符合购买者意向的最优选择, 比如, 购房者对2和5号楼盘感兴趣, 这种方法给出了更好的选择1。

4 结 语

本文的主要目的是构造一种近似概念,从而能够从形式背景中提取出更有利于实际决策的信息。首先,在文献[15]的基于k-阶关系近似概念的研究基础上,提出了k级近似概念;其次,通过k级近似概念,为非外延类赋予合理的语义解释,并且将这种语义解释应用于推荐。最后,将k级近似概念推广到任意对象子集,从而给出了一种等价类的排序的方法,使其语义解释更适合实际推荐工作。进一步,我们还可以在三支概念[17]上探究非外延类的性质及特点,并获取更深层的信息。