基于IGA-IBP算法的高速公路逃费预测
2018-12-22李松江李岩芳王艳春宋小龙
李松江,周 舟,李岩芳,王艳春,宋小龙,王 鹏
(长春理工大学 计算机科学技术学院,吉林 长春 130022)
0 引 言
当前,对于高速公路恶意逃费问题,研究学者都有着不同深入的研究。薛[1]将数据挖掘技术引入收费稽查中并建立系统模型;赵等[2]采用聚类分析、判别分析和逻辑回归分析融合的方法;吴等[3]利用数据挖掘k-means技术研究高速公路的逃费问题。
高速公路收费数据量大且复杂度高,收费管理方式缺乏完善[4],传统的算法难以处理。对于高速公路逃费的预测问题,在结合高速公路的收费数据特征下,本文提出一种基于改进的遗传算法和优化的神经网络的IGA-IBP算法模型,首先选取6个黄金分割变异算子,迭代出适应度函数的最优解,得到最优初始权重值;然后分步动态调整神经网络模型的学习率,考虑隐含层和输出层学习率时加入上一次学习率的变化影响,这使得模型可以加快收敛速度和减小误差,对高速公路收费数据,利用ReliefF算法[5]提取出车辆逃费行为的主要特征作为该算法的输入,建立神经网络模型实现对车辆逃费预测。
1 IGA-IBP神经网络模型
遗传算法通过模拟自然进化过程的生存方式,是一种随机性的全局优化算法[6],经过选择、交叉和变异后可以得到最优解。经典的遗传算法容易陷入“早熟”[7],不能及时跟踪网络的反馈信息,搜索速度慢,处理高速逃费预测这种非线性问题稳定性较差。传统的BP算法满足不了高速公路收费数据的复杂性,全局搜索能力差,输入层、隐含层和输出层在权值和阈值修正过程中学习率β总是一成不变。当β过小时,模型调整较小,逃费预测速度过慢;当β过大时,预测误差函数值较高,容易在最优解处发生振荡,导致出现局部最优解以致模型难以收敛[8]。针对此问题,本文提出IGA-IBP算法,通过改进遗传算法的变异算子、分步调整BP神经网络各层间的学习率并考虑前一次学习率影响因子,以及动态调整车辆行驶时间来提高算法对高速公路逃费的预测准确率和稳定性。
1.1 算法设计
遗传算法中的变异算子对种群优化起重要作用,种群如果失去多样性,则过早收敛[9],优化质量低。因此遗传算法优化时,如何维持种群的多样性是关键问题。本文为了保持种群多样性,在基本的两个黄金分割点基础上提出多个黄金分割变异算子优化传统遗传算法,可以获得进化中的优良新个体,保持群体多样性。对于多元优化自变向量分量xk,k=1,2,…,n,这2n-1条边界按照式(1)的黄金分割法的思路寻求新的迭代空间会大大缩小计算量,考虑到种群的迭代过程变化趋势,本文选取6个黄金分割变异算子,种群中的个体迭代可以如下表示
(1)
遗传算法进化过程中群体向着更优的目标函数进化,第m代个体进化可以按照以上6种原则进化。对种群个体进行迭代,将待求解的目标函数转化为适应度函数,适应度函数根据平均值和方差比构建,适应度函数越大个体越好,适应度函数越小个体越差,选择出6个黄金分割点的适应度函数的最大值,即
(2)
依次迭代个体的适应度函数与上一代的最优解比较,若当前解优于上一代最优解则替换原来的最优解,否则继续迭代个体并判断找出最优解。替换原来最优解后,继续迭代多次比较,最终找出目标最优解。
传统的BP神经网络学习率与误差函数关系较大[10],其学习率在运算过程中不变会影响模型的性能。针对这种现象,本文采用一种分步动态调整不同层间学习率的方法,即分别对隐含层学习率β1和输出层学习率β2调整,并考虑前一次学习率的变化影响。在此方法中,隐含层学习率β1(m)和输出层学习率β2(m)修改公式如下
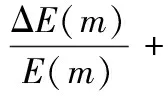
(3)
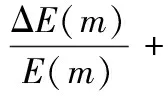
(4)
式中:β1(m+1)表示在第m+1次迭代时训练样本的隐含层学习率,β2(m+1)表示在第m+1次迭代训练时训练样本的输出层学习率,ΔE(m)/E(m)表示训练样本在第m次迭代训练时的均方误差变化率,μ是常数,取值范围为[0,1],本文实验调优后取值为0.6,Δβ1(m-1)表示m前一次的隐含层学习率,Δβ2(m-1)表示m前一次输出层的学习率。
当ΔE(m)>0时,表明误差函数增大,输出预测值与期望值相差过大,权值调整偏大,需要减小输入层到隐含层的权重以及隐含层到输出层的权重。同时可以看出,β1(m+1)<β1(m),β2(m+1)<β2(m),β1(m)和β2(m)减小,可以加快收敛速度;当ΔE(m)<0时,表明学习误差减小,输出预测值与期望值相差不大。因此可以适当提高输入层到隐含层和隐含层到输出层的权重。由于此时误差很小,ΔE/E比ΔE要大很多,因此当β1(m+1)>β1(m),β2(m+1)>β2(m),β1(m)和β2(m)增大,收敛速度同样也加快。在学习率变化的同时考虑前一次学习率的影响,使得学习率连续变化,增强算法的可靠性。
1.2 IGA-IBP算法操作过程
通过1.1节分析,IGA-IBP算法如下,其具体实现步骤如下:
(1)编码方式和种群初始化
考虑权重值的精度要求高,因此采用浮点数编码方式。随机产生一组具有N个个体的种群M=(M1,M2,…,Mn)T,种群中每个个体代表一个神经网络的初始权值分布,个体的长度为神经网络权值的个数,即
L=m×n+n×h+n+h
(5)
其中,m表示输入层隐含层神经元个数,n表示隐含层神经元个数,h表示输出层神经元个数。
(2)确定适应度函数
计算初始种群中每个染色体的适应度值,并定义适应度函数fit(x)。待求解的目标函数f(x)转化为适应度函数fit(x),目标函数求最大化问题时,fit(x)=f(x),解最小化问题时,fit(x)=-f(x)。
(3)个体选择
个体的选择即是个体的概率值计算,采用轮盘赌选择,每次为新种群挑选出新的个体,公式如下
(6)
其中,k为种群个体数目。
(4)交叉操作
使用交叉概率pc对两个个体进行交叉操作,产生两个新的个体。交叉概率计算公式如下
(7)
式中:f表示个体的适应度,favg表示种群中所有个体的平均适应度,fmax表示种群中个体适应度的最大值。通常pc1取0.8,pc2取0.6。
(5)变异操作
分别计算式(2)变异点的适应度值,找出最大点。用变异概率pm计算式(1)优化产生新的个体。根据经验本文初始化变异概率pm=0.08。
(6)循环终止操作
在遗传算法优化神经网络权值中,达到最小目标函数或者完成迭代次数后训练停止,否则重复步骤(2)~步骤(5)。
(7)将改进后的遗传算法操作完成后得到的最优个体作为神经网络的初始权重值,然后按1.1节中的改进的BP算法对神经网络进行训练,得到预测结果。
算法流程如图1所示。
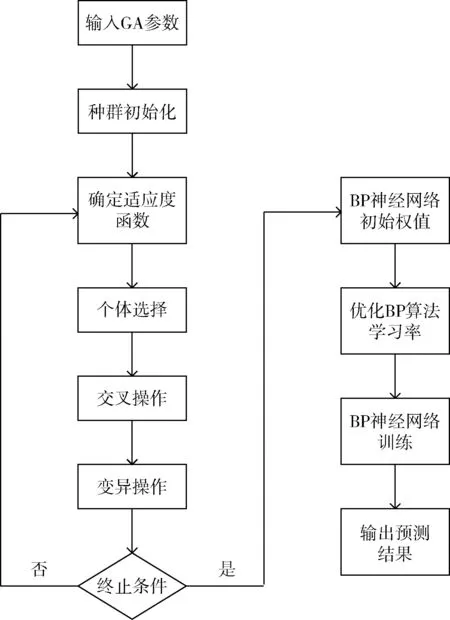
图1 算法模型流程
2 IGA-IBP逃费预测模型数据分析
2.1 特征选取
高速公路收费数据包含许多特征属性,见表1,算法输入相关性不大的特征会降低模型的准确率,因此需清洗脏数据,选出合理的特征属性[11]。

表1 特征属性标号及对应的名称
本文采用ReliefF算法处理逃费问题的IGA-IBP算法的特征选择问题,得到的32个属性特征权重值如图2所示。

图2 不同特征属性权重值
由图2可以看出,收费数据特征属性值的权重不同,标号3,4,7,9,10,12,13,14,18,23,24,30的权重值比较高,均在0.08以上,这些特征属性对于逃费预测判断至关重要。而其它特征属性的权重值较小,属于脏数据,可以删除。因此,本文选择车辆入口牌照号、车辆出口牌照号、出站车型、出口日期、出口时间、入口日期、入口时间、IC卡编号、入口车型、轴数、轴总重、收费额作为IGA-IBP模型的特征向量。
2.2 车辆动态行驶时间计算
司机在高速公路上驾驶速度不一,因此车辆到达收费站的时间不同。有司机因为“跑长买短”出现超时情况,但是实际中一些超时的异常情况跟逃费行为无关,例如在服务区停留休息、道路发生车祸和天气原因等。因此选定一个合适的时间阈值对于模型的预测准确率有很大影响。高速公路的行驶时间主要由两方面决定:在非拥挤道路上的行驶时间和堵车排队等候时间。将路段S分成AB和BC两段,AB为非拥挤路段长度,BC为拥挤排队路段长度,若无拥挤现象,则S=AB;若发生拥堵情况,则BC=S-AB,其具体表达式如下

(8)
其中,mi表示排队的第i种车的数目,di表示第i种车所占的空间长度,n表示排队的车的类型数。非拥挤道路中,假设第i种类型的车辆行驶速度为vi,则车辆在路段AB上的行驶时间为
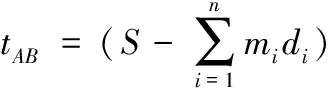
(9)
车辆在堵车排队向前移动直到排队结束的时间是动态变化的,排队时间可以认为车辆C前面排队的每辆车与其相邻的前一车向前移动的时间间隔λi之和,可以表达为

(10)
式中:L代表车辆C到达排队队尾时车辆的排队队长。因此,路段S的行驶时间为

(11)
2.3 数据归一化处理
从原始高速公路数据库中通过结构化查询语句获取的数据,具有不同的量纲和量纲单位,这往往会影响数据分析的结果,因此需要对数据预处理。本文只需对轴总重数据归一化,采用min-max标准化,对原始数据线性变换,使结果值映射到(0,1)之间。其公式如下

(12)
其中,X′为数据归一化结果,X为原始数据样本,Xmax为样本数据中的最大值,Xmin为样本数据中的最小值。根据式(12)计算得出轴总重的归一化数据,见表2。
2.4 模型参数选择
根据高速公路收费数据中已有的车辆通行时间,通过式(11)得出动态车辆行驶时间,并与车辆在两站之间行驶的平均时间比较,如果未超时用0表示,否则用1表示;进站车牌和出站车牌相同用0表示,否则用1表示;进站车型和出站车型相同用0表示,否则用1表示;车辆根据轴数和载重量判断是否超重,如果未超重用0表示,否则用1表示;车辆进站和出站的通行卡相同用0表示,否则用1表示;收费额比正常通行费低用1表示,正常用0表示。高速公路收费数据处理后的神经网络模型所需特征向量见表3。

表2 轴总重归一化前后数据
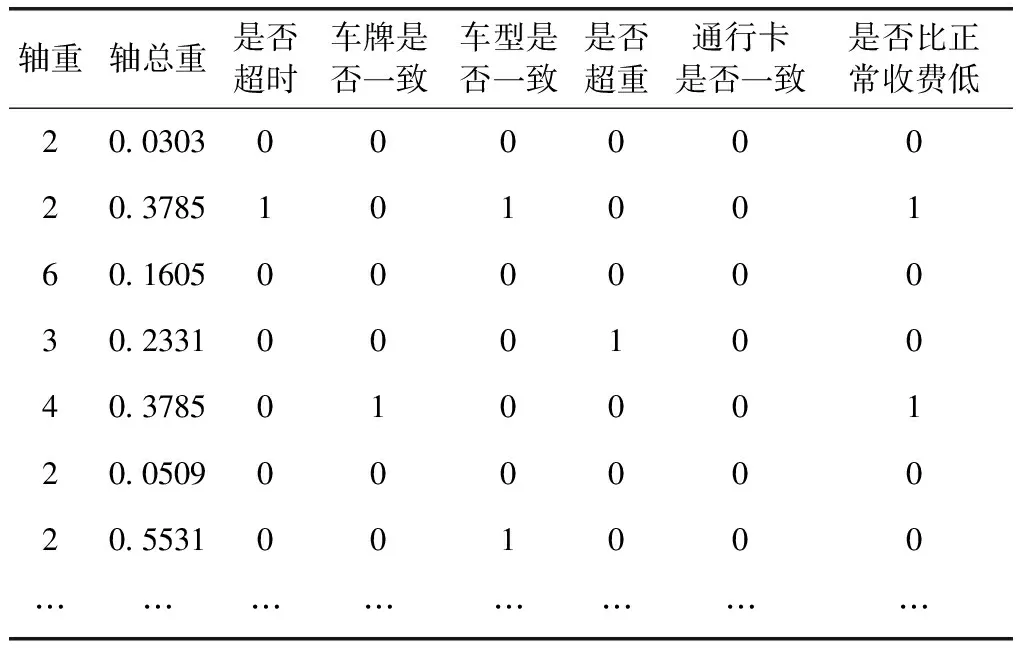
表3 神经网络特征向量
依据上述描述,输入层特征个数为7个,输出层特征个数为1个。根据多次调试后,三层结构对于两层结构预测结果相差不明显,但是训练时间和复杂度明显提升。因此,隐层最终选择两层。隐藏层神经元个数参考式(13),利用试凑法最终确定第一层神经元个数为26,第二层神经元个数为14
(13)
式中:n为隐层神经元个数,m为输入层神经元个数,s为输出层神经元个数,a为一个0~10之间的常数。本文经过多次调优后,n确定为11。学习率大小调整依据1.1节方法调节输入层到隐含层和隐含层到输出层的学习率。对于二分类预测和输出在[0,1]的特点,激活函数选择非线性函数sigmoid,损失函数使用交叉熵函数。
3 实验与分析
3.1 实验数据
实验数据采用吉林省2014年的数据,根据“留出法”和实例完整度将总共筛选出的846 533条数据划分成两部分,80%作为训练集,20%作为测试集。
3.2 评价指标
实验通过算法模型的准确率这个量化的指标对神经网络模型进行评价,计算公式如式(14)所示,对于分类问题,召回率也是重要的评价指标,即所找出的逃费数量占样本总数的比例,对于召回率其计算公式如式(15)所示
(14)
(15)
其中,TP(true positive)表示将正类预测为正类数,FN(false negative)表示正类预测为负类数,FP(false positive)表示负类预测为正类数。
综合考虑准确率和召回率,计算公式如下
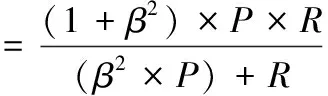
(16)
在不同问题中的准确率和召回率重视程度不同,本文希望尽可能的少遗漏逃费车辆,召回率更重要,因此确定β>1。对于模型的运行速度,可以通过平均检测时间(MTTD)指标,MTTD值越小,模型预测速度越快。
均方根误差(RMSE)、平均绝对误差百分比(MAPE)和相关系数R2可以用来进一步验证模型的性能。其公式如下
(17)

(18)
(19)
其中,n表示数据集,xm表示测得的数据值,xp表示预测值,xmean表示均值。
3.3 实验结果与算法对比
根据IGA-IBP算法结合TensorFlow1.0框架对 2014年的高速公路收费数据进行训练。数据分类预测模型算法较多,为了验证IGA-IBP算法预测结果的性能,本文选取了决策树(decision tree,DT)、K最近邻(K-nearest neighbor,KNN)、IGA-BP和GA-IBP算法的预测模型与提出的IGA-IBP模型对此。
不同算法模型在高速公路逃费预测方面的准确率如图3所示。从图中可以看出,5种算法模型均有较高的准确率,但算法中的IGA-IBP算法准确率最高,到达95.1%。因为该算法动态调整学习率使得损失函数最优,改进的遗传算法加快网络结构收敛速度,同时也优化了BP神经网络的初始值。

图3 不同算法模型准确率对比
不同的需求需要采取不同的方法,本文根据实际情况以及3.2节的描述,在β的取值范围中,令β=2,根据式(16)计算各模型的Fβ值。表4是各模型在训练集上Fβ和MTTD参数对比。对于IGA-BP算法、GA-IBP算法和IGA-IBP算法中的GA存在随机操作,每次操作得到的数据不同,例如运行时间等,因此,本文实验室结果为多次实验后的平均值。

表4 算法模型参数对比
从表4可见,各组中IGA-IBP算法的Fβ值是最大的,表明IGA-IBP模型在准确率和召回率两方面是最平衡的,预测时间MTTD为215 s,预测耗时小,模型运行速度快。KNN模型的Fβ值相比其它模型最低,运行速度最慢,可见,针对本文数据预测,KNN模型性能最差。IGA-BP和DT模型Fβ值和运行速度比较接近,两者表现整体在训练集上不相上下,GA-IBP模型虽然Fβ值较高,但是运行时间过长,原因是GA-IBP模型全局搜索能力较弱。
对于各个算法模型的在训练集和测试集上的参数性能对比,见表5。
从表5可以看出,考虑预测模型的RMSE值时,DT、KNN、IGA-BP、GA-IBP和IGA-IBP测得的值分别为0.47、0.48、0.36、0.22、0.20,IGA-IBP均方根误差最小,对于MAPE,IGA-IBP的Test值为4.14也是最小的,这些值说明了IGA-IBP偏差程度很小,收敛速度快,具有很高的一致性。另一方面,预测模型的相关系数R2,DT、KNN、IGA-BP、GA-IBP和IGA-IBP对应的值分别为0.71、0.63、0.76、0.88、0.91,从此处指标可以说明IGA-IBP训练值和预测值有很高的相似度,预测逃费的值与测量值更接近,得出的预测结果更准确。

表5 不同算法模型的评价比较值
通过以上分析,IGA-IBP比其它算法模型在综合评价指标Fβ方面更优,在高速公路逃费数据的训练集和测试集方面两者误差比很小,而精确度高,IGA-IBP神经网络加快了收敛速度,较高的相关系数对于IGA-IBP则表现出模型具有很好的泛化能力。因此将IGA-IBP模型运用在高速公路逃费实际预测上是可行的。
4 结束语
本文基于高速公路传统逃费预测方法准确率和可靠性低下,人工稽查效率低下、漏查等问题提出了IGA-IBP算法,首先优化遗传算法,提出6个黄金分割变异算子,找出最优初始权值;其次,改进BP神经网络算法,分步动态调整输入层和隐含层之间的学习率,考虑上一次学习率的变化影响,而不同车辆到达收费站的行程时间特征属性不同,因此需动态计算车辆行驶时间。实验结果表明,本文提出的IGA-IBP算法调高了学习速度和预测准确率,在RMSE、MAPE和R2性能均优于传统的算法,对交通部门的决策有着重要的意义。
