基于曲率特征与改进的RANSAC策略的图像匹配算法

王 瑜，禹秋民

(1.汉江师范学院 计算机科学系，湖北 十堰 442000；2.湖南师范大学 数学与计算机科学学院，湖南 长沙 410006)

0 引 言

虽然目前图像匹配[1,2]方法多种多样，但常用的图像匹配方法主要是模板匹配法以及特征匹配法。如谢志江等[3]提出了旋转不变性图像模板匹配快速算法，基于图像的3种不同特征，分两步精确快速地完成了统计匹配运算，实验结果验证了其算法的有效性，但是该基于模板匹配的方法难以顾全图像的细节信息，使得匹配图像中存在较多漏匹配的现象。又如Shen等[4]利用归一化互相关机制与SIFT来设计一种用于遥感图像的匹配方案，测试数据验证了其方案的可靠性，但SIFT机制容易产生伪特征点，导致其鲁棒性与准确匹配数量较低。对此，文献[5]提出了一种采用轮廓向量特征的实时图像匹配方法，依据待测图，优先剔除大量目标非潜在位置区域，仅对剩余少量区域进行计算，非最高层则进行同步局部搜索图像区域构建及匹配，实验结果验证了其算法的优异性，但是该算法计算复杂度较高。

对此，本文提出了曲率特征联合RANSAC策略的匹配方法。借助Harris机制，对图像的特征点进行检测，接着利用检测到特征点的尺度特征构造特征矩阵，用于建立特征点优化模型，从而剔除伪特征点以及冗余特征点，提高了算法的匹配正确度与效率。通过Haar小波获取特征点的主方向，然后建立同心圆区域，按照方向指针求取圆内的曲率特征，以获取特征向量，进而获取较低维度的特征描述符，从而构建了相应的描述符。最后，借助几何距离度量机制来提纯匹配准确性。

1 本文图像匹配算法设计

所提的基于曲率特征与改进RANSAC的图像匹配过程如图1所示。其主要有4个阶段：特征点提取；建立描述符；特征点匹配；匹配提纯。

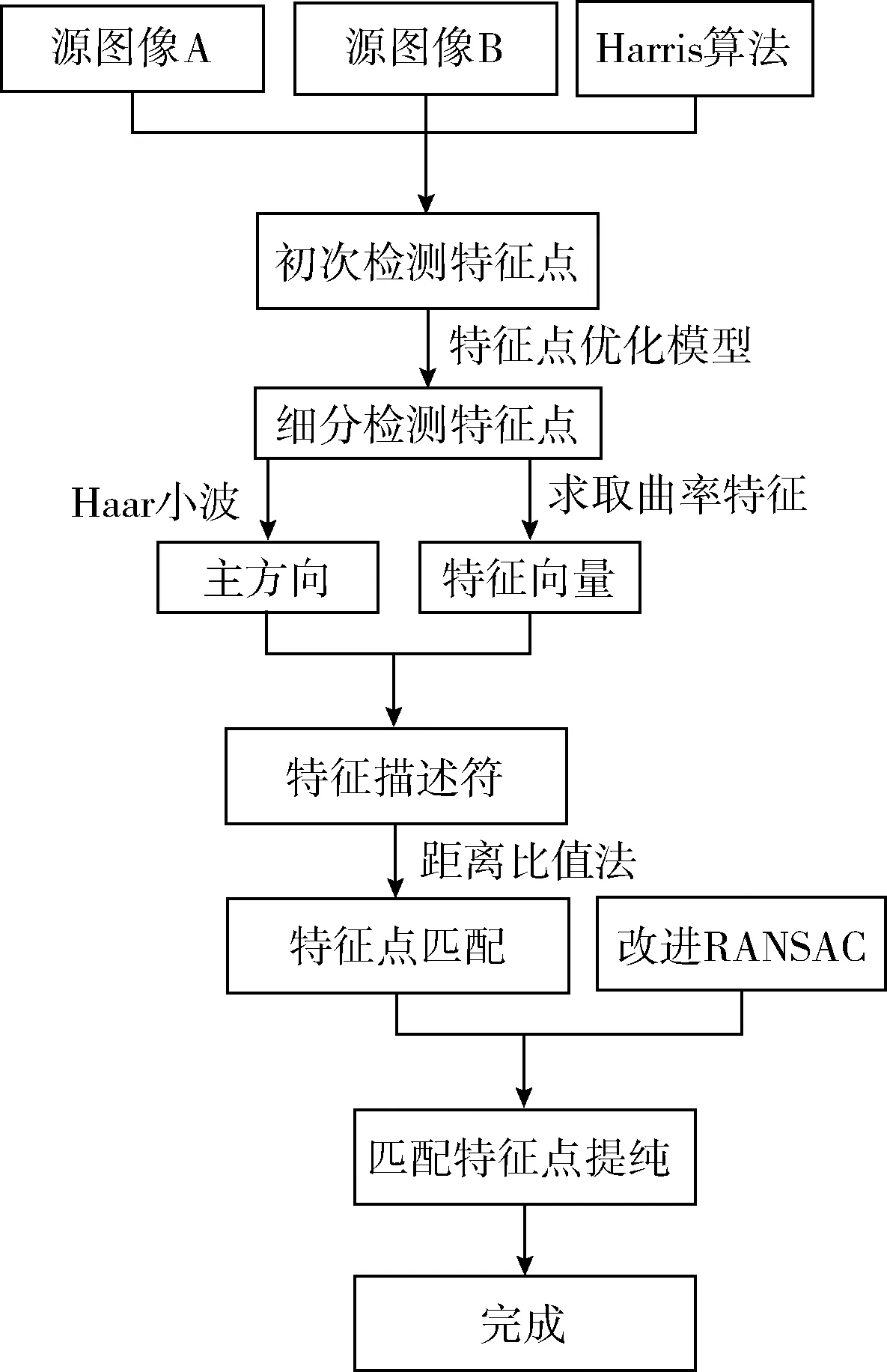
图1 所提算法的匹配流程

1.1 特征点检测

SUSAN算法、Moravec算法、Harris算法以及MIC等算法是目前用的较多的特征点检测方法。这些检测方法中Harris算法的检测精度较高，但Harris算法检测的特征点中也会存在少量伪特征点以及冗余特征点[6]。为了获取到较为理想的特征点，本文首先采用Harris算法对图像进行初次特征点检测，利用检测到特征点的尺度特征构造特征矩阵，用于建立特征点优化模型，再利用该模型剔除伪特征点以及冗余特征点，从而获取到纯度较高的特征点。

Harris算法通过对像素点的亮度变化进行度量，依靠特征点判定模型对图像特征点进行检测，主要过程如下。

对于一幅图像I(x,y)，其对应的自相关函数M可表述为[7]

(1)

式中：E表示高斯滤波器，J和K分别表示图像对于x和y的偏导数，E、J和K分别表述如下

(2)

(3)

(4)

通过自相关函数M构成的特征点判定模型为[8,9]

(5)

式中：Det(M)表示M对应的行列式，Tra(M)表示M的迹，α为常数，不失一般性，在此取值为0.05。

对图像I(x,y)中所有像素点按式(6)进行计算，当某一像素点计算所得的P值大于预定阀值FP时，则将该像素点判定为特征点。

由于Harris算法检测的特征点中存在少量伪特征点以及冗余特征点，在此将建立特征点优化模型对Harris算法检测到的特征点进行优化。

设g(i,j,φ)为Harris算法检测到的任意一个特征点，其坐标为(i,j)，其尺度值为φ，则该点对应的特征矩阵Q为

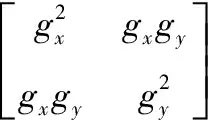
(6)

式中：T(i,j)为加权函数

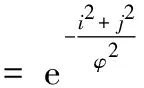
(7)

通过特征矩阵Q形成的特征点优化模型为

U=Det(Q)-0.04Tra2(M)

(8)

当特征点g(i,j,φ)对应的U值小于阀值FU时，则认定该特征点为伪特征点或冗余特征点，将其剔除。

阀值FU为与U值相关的自适应模型

(9)

其中，S为Harris算法检测到的特征点总数。

1.2 构建描述符

本文采用求取Haar小波响应的方法获取特征点的主方向，接着建立同心圆区域，求取圆内的曲率特征，形成特征向量，生成低维度的特征描述符。

选取任意尺度为θ的特征点h(xc,yc)作为圆心，并构造一个半径为6θ的圆。采用4θ大小的Haar小波，求取该圆在x和y方向上的Haar小波响应值。再构建一个角度为60°，以特征点为原点的扇形窗口[10]。将此扇形窗口在圆内旋转一周后，求取扇形窗口内Haar小波响应值。最大Haar小波响应值对应的方向被确定为主方向δ[11,12]。

以两个像素点为步长，构建4个同心圆，如图2所示。再以主方向为起点，30°为步长，构建方向指针，形成12个方向指针。对每个同心圆按照这12个方向指针求取曲率特征。曲率特征的求取过程如下：

对于特征点h(xc,yc)，其主方向为δ时，可通过下式求取曲率角度η

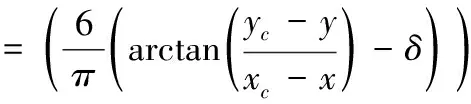
(10)

通过曲率角度可构造曲率特征模型

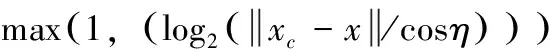
(11)

式中：σ为加权系数，其计算方法如下

(12)

将每个同心圆求到的曲率特征值从大到小进行排序，选取前12个曲率特征值。将第1个同心圆选取出的12个曲率特征值作为特征向量中第1到第12个元素，将第2个同心圆选取出的12个曲率特征值作为特征向量中第13到第24个元素，由此对4个同心圆中选出的48个曲率特征值进行排序，便可得到一个48维的向量。将此48维向量进行归一化处理后，便得到了一个48维的特征向量，从而生成了48维的特征描述符。

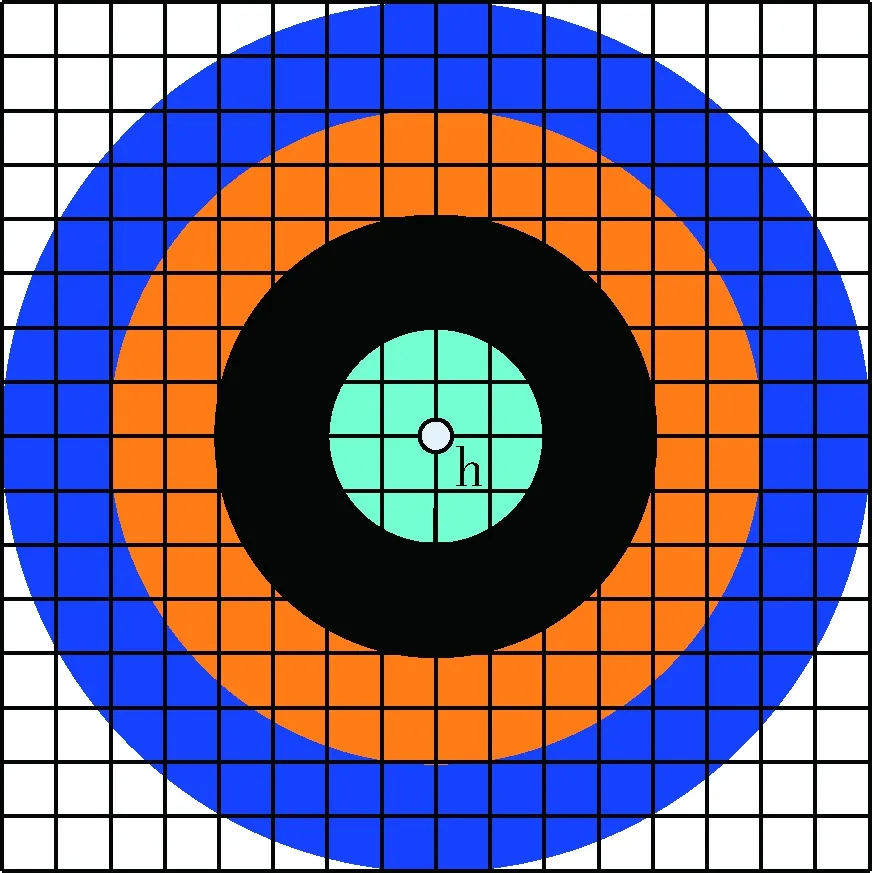
图2 构造的同心圆

1.3 特征点匹配

在此利用特征点的欧氏距离，通过距离比值的方法，实现特征点的匹配，具体过程如下。

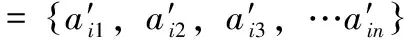
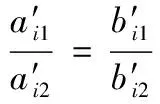
(13)

1.4 匹配特征点提纯

最后，本文构造几何距离度量模型，替换传统RANSAC算法中的距离度量模型，对RANSAC算法进行改进，剔除错误匹配特征点，实现匹配特征点提纯。

在传统RANSAC算法中，利用距离度量模型多次提取最小点集，对距离度量模型中的参数进行调整，再通过调整后的距离度量模型检测出错误匹配特征点[15]。由于传统RANSAC算法中距离度量模型过于简单，导致其不能对错误匹配特征点进行较为完全的检测[16,17]。对此，本文将利用匹配特征点集的平均值，构造几何距离度量模型，对传统RANSAC算法进行改进。

(14)

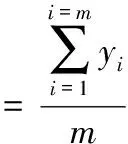
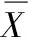
再根据MA来定义几何矩阵R

(15)

根据上述几何矩阵R，可计算两个匹配特征点xi和yi的几何距离为

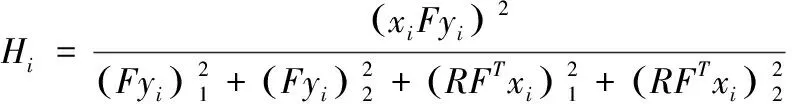
(16)

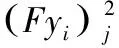
xiFyi=0

(17)

将式(16)替换传统RANSAC算法中的距离度量模型，便可通过改进的RANSAC完成匹配特征点的提纯。

2 仿真实验

仿真实验在IntelCore i53.4 GHz处理器、500 GB硬盘、操作系统为Windows XP的PC机上进行，在VS2008软件上编程实现算法。选取文献[19，20]中的图像匹配方法作为对照组，以体现本文算法的有效性。

2.1 匹配测试

图3为所提方案与文献[19,20]对组合变换图像的匹配测试。图4为所提方案与文献[19,20]对旋转攻击图像的匹配测试。依据图3可知，本文技术、文献[19，20]算法的匹配准确度都可接受。但是，在文献[19，20]算法的匹配效果图中，分别如图3(c)和图3(d)所示，存在的错误匹配点比本文算法的匹配效果图中(图3(e))都多。说明本文算法具有较好的匹配正确度以及匹配精度。通过对比图4中不同算法的匹配效果图可见，本文算法的匹配效果图中(图4(e))，比文献[19]中算法的匹配效果图中(图4(c))，以及文献[20]中算法的匹配效果图中(图4(d))拥有更高的配对精度。原因是所提方案借助Harris机制来设计特征点优化方法，使其提取的特征点更为稳定。同时本文还利用特征点的欧氏距离，通过距离比值的方法，实现特征点的匹配，进一步提高了算法的匹配精度以及鲁棒性能。

图3 3种算法对经过噪声+模糊干扰的图像匹配的效果

图4 3种算法对经过旋转变换的图像匹配的效果

2.2 客观评价

从牛津大学机器人实验室的数据集中任选6组图像作为测试对象[21]。测试过程中将特征点的总数量设置为260个，通过对照组算法以及本文算法对这6组图像进行匹配测试，并将测试过程中不同算法的总耗时、正确匹配特征点数量以及错误匹配特征点数量进行记录，通过对比记录结果对不同算法进行客观评价。

不同算法的客观评价参数统计结果见表1。从表1中可见，本文算法的总耗时为15.5415 s，为最少耗时。本文算法的正确匹配特征点数量为182个，为最多正确匹配数，本文算法的错误匹配特征点数量为14个，为最少错误匹配数，说明从客观评价上看，本文算法具有较好的匹配性能。因为本文采用了建立同心圆区域，按照方向指针求取圆内的曲率特征来形成低维描述符，有效减小了复杂度。同时，所提方案还构造了几何距离度量模型，对RANSAC策略实施，以提纯配准正确率。文献[19]算法采用的SIFT算子容易提取目标中的不稳定特征，且其形成的描述符达到128维，使得算法的匹配效率较为低下，匹配正确度不佳。文献[20]中算法采用SURF提取特征点，并通过FLANN方法对特征点进行双向匹配，由于提取的特征点中没有对伪特征点以及冗余特征点进行处理，导致算法的匹配耗时较多，匹配正确度不高，同时FLANN方法一种双向匹配机制，使其复杂度很高。

表1 不同算法的客观评价参数统计结果

3 结束语

为了改善图像的匹配准确度，本文通过改进RANSAC机制，设计了新的匹配技术。借助Harris算子来获取图像特征点，利用特征点的尺度特征构造特征矩阵，用于建立特征点优化模型，检测出伪特征点以及冗余特征点并剔除，实现了特征点的再次细分检测。利用Haar小波响应方法获取特征点对应的主方向，接着建立同心圆区域，按照方向指针求取圆内的曲率特征，以获取特征向量，进而获取较低维度的特征描述符。通过特征点的欧氏距离比值，实现特征点的匹配。利用匹配特征点集的平均值，构造几何距离度量模型，对RANSAC算法进行改进，剔除错误配对现象。仿真数据彰显了本文方案的可靠性与优异性。