分段弱选择自适应正交匹配追踪算法
2018-12-22秦伟萌
王 烈,罗 文,秦伟萌
(广西大学 计算机与电子信息学院,广西 南宁 530004)
0 引 言
压缩感知(compressive sampling,CS)[1,2]理论,作为近年来一种全新的理论引起了广泛的关注。由于传统的奈奎斯特采样定律运算时间长,采样数据量多,存在大量的冗余,且采用先采样后压缩的方式,既浪费了传感器又浪费了采样和计算的成本和时间。比较之下,压缩感知针对稀疏信号或者在特定域上的稀疏信号,只需要采样极少量的信号值,同时对数据进行采集和压缩,从而减少了软、硬件的运行成本和时间。这一系列的优势使得压缩感知能在信号处理领域有着更广泛的前景[3]。
压缩感知理论主要分成3个部分:信号稀疏矩阵的设计部分、观测矩阵的设计部分和重构算法的设计部分,其中重构算法是压缩感知理论研究的重要方面[4],关键是如何从低维的数据中快速精确的重构出原始信号。目前重构算法可以大致分为几个大类:组合优化算法、凸优化算法和贪婪算法等[5]。如李小静等提出的一种改进的迭代硬阈值算法(MIHT),是对经典的采用迭代硬阈值方法(IHT)重构信号的改进[6]。如陈小玲等提出的基于梯度投影sEIRLS算法,是对经典的基于迭代加权最小二乘方法(IRLS)重构信号的改进[7]。如孟祥瑞等提出的基于正则化正交匹配追踪算法的改进(BRAMP),是对经典的基于正交匹配追踪算法(ROMP)的改进[8]。如刘杰平等提出的基于DCT频带能量的压缩感知重构算法,通过对图像分块DCT后,采用投影Landweber算法对图像重构[9]。在这些算法中,由于贪婪算法设计结构简单,运算量小,重构效率高等特点,使得贪婪算法应用最广[10]。最先经典的贪婪算法是正交匹配追踪(orthogonal matching pursuit,OMP)[11],这类算法设计简单,但在信号重构时会出现过匹配的现象,且重构质量不高;随后在OMP基础上提出了一些改进算法,如分段正交匹配追踪(stage-wise OMP,StOMP)[12],利用特定阈值通过多次迭代选择原子更新支撑集来重构原信号,但都需要大量的测量量才能达到较好的效果,故影响了重构效率;稀疏度自适应匹配追踪(sparsity adaptive MP,SAMP)[13],虽然能在稀疏度未知的前提下进行精确重构,但SAMP的重构速度较慢,效率低。本文在StOMP算法分段思想的基础上,通过SAMP的自适应思想和弱选择标准相结合,提出一种基于分段弱选择自适应正交匹配追踪(stage-wise weak selected adaptive matching pursuit,SWAMP)重构算法,该算法首先对原二维信号进行分块滤波处理,再在各分块图像上,通过自适应设定阈值不断优化初始候选集,利用弱选择标准不断更新支撑集,极大提高了重构精度和效率。实验结果表明,该算法重构复杂度低,重构效果好。
1 压缩感知与重构算法
1.1 压缩感知的重构模型
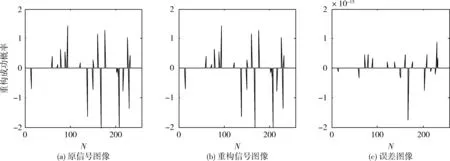
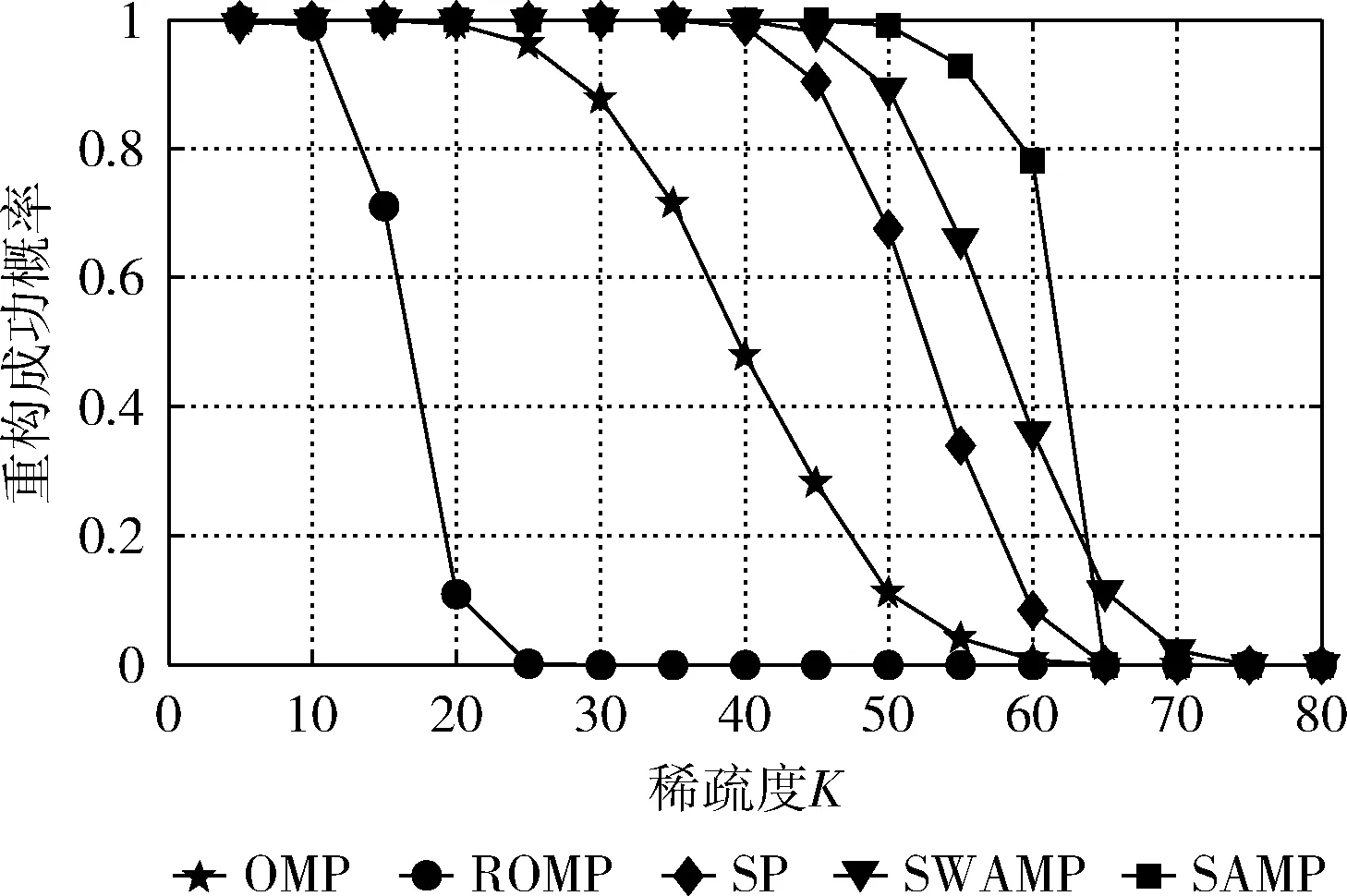
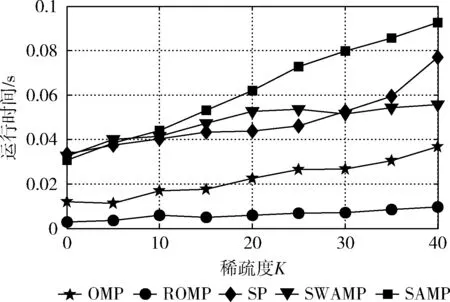
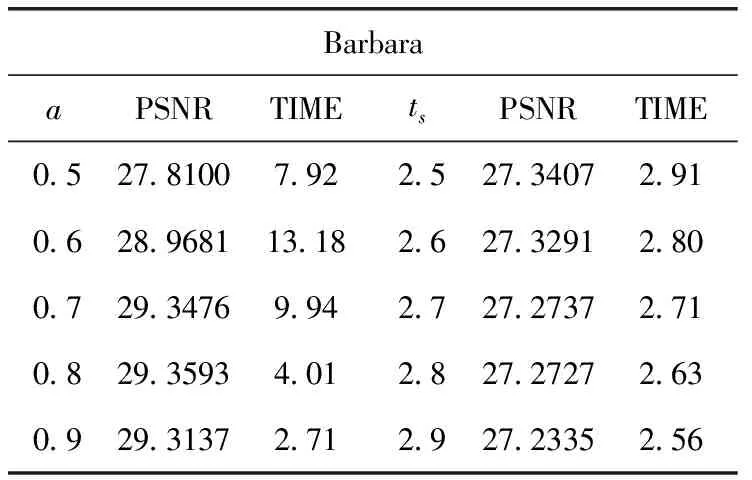
假设原始信号x的长度为N,观测信号y的长度为M,测量矩阵为Φ的大小为M×N(M (1) (2) 传统的贪婪算法根据式(2)的最小1-范数问题来精确重构原信号,结合考虑贪婪算法的不同特点,本文重点讨论在稀疏度未知条件下的重构算法。分段正交匹配追踪(StOMP),一种基于OMP的改进方法,通过设定阈值,从残差r与观测矩阵Φ的内积中选取大于设定阈值的一组原子,通过不断迭代最终逼近原信号。另一个最具代表性的是稀疏度自适应匹配追踪(SAMP),在稀疏度K未知的情况下,通过设定一个可变步长,利用自适应性通过残差判定控制步长大小从而逐步迭代逼近原始信号。利用StOMP与SAMP的突出优势,引入弱选择标准,本文提出了采用分段弱选择自适应正交匹配追踪算法(SWAMP),能够在稀疏度K未知的情况下保证重构信号的有效性和稳定性。 现流行的一些算法,将整幅图像作为一个整体,故在重构过程中,计算复杂度较高,随机观测矩阵存储量大,且重构图像质量差等问题,使得这些算法很难实际应用。因此,在2007年GAL.L等提出,将整个图像分成多个块,通过针对块的采样和重构方法,使得降低计算复杂度,通过引入维纳滤波器以消除图像分块所导致的块效应。为了兼顾图像的重构质量和CS的计算开销,借鉴BCS-SPL实现技术[16],本文提出的算法对一个图像整体进行分块预处理,后采用维纳滤波器消除块效应,进而提高重构效率。 对于一维信号测量矩阵直接采用高斯随机矩阵,但对于二维信号,若直接对整体图像进行稀疏处理,如512×512的图像信号,则N的长度有106等级,故会影响重构效率。针对CS在二维图像中的应用限制,采用分块CS技术(block-based CS,BCS),把图像分成B×B块。使得重构对象不再是512×512大小的图像整体,而是分块后B×B大小的块图像。 采用Z行扫描技术对二维图像进行扫描,对扫描后图像的第i个图像块用xi表示,那么有yi=Φψxi。其中测量矩阵Φ的大小为M×B2, 其中B的大小根据图像的重构速率和重构质量要求综合决定,本文中取B=32。ψ为稀疏矩阵,本文采用小波变换对信号进行稀疏表示。 在SAMP重构原始信号的过程中,算法的每次迭代都是依据残差r与观测矩阵Φ的相关性,挑选步长L个原子最值的角标选为候选集J,通过候选集J重建出信号并计算出与原信号之间的残差r,再通过残差判定控制步长进一步选择更匹配的原子,从而更新候选集,直到满足停止迭代条件,完成重构。然而,对步长L的选取直接影响到原信号重构的效率和质量,如果步长过大,则可能导致重构失败[17],而步长过小,则会影响重构效率。此外,通过步长来选择原子的方式不能充分体现不同的残差r与观察矩阵Φ中各个原子间相关性的差异。 (3) 其中,j∈J。ts的取值范围为2 由初始步长得到初始候选集,而初始候选集不能直接重构出原信号,本文提出的重构算法通过引入弱选择标准更新候选集,最终重构出原信号。 令g=ΦTr,则g中第k个元素gk就表示原子向量vk与残差r的内积,即 {gk≥a·maxgk} (4) 其中,k∈J,a∈(0,1)。特别的,当a=1时,只选取一个相关性最大的原子角标存入候选集,与OMP相同。SWAMP算法选取所有满足式(4)的原子对应的角标存入候选集J中,则完成了一次对原子的弱选择。a值的大小决定选择原子的个数。当a取值较小时,步长较大,运行效率高,但影响重构质量;而a取值较大时,重构质量较高,但运行效率低。针对本文提出的重构算法,通过验证不同取值下的重构质量与运行时间,当a=0.8时,重构效果最好。通过弱选择,使得SWAMP能有效的依据残差r和观测矩阵Φ中各相关性的差异选取原子。 将弱选择标准引入StOMP中,结合SAMP的自适应性,在不需要已知稀疏度的前提下,利用残差r和观测矩阵Φ之间相关性的差异挑选原子,且通过自适应性调节阈值大小,更有效表示出原子集,进而提升重构算法的有效性和稳定性。 本节将给出分段弱选择自适应正交匹配追踪算法的具体步骤,算法停止迭代条件为残差值小于ε。 输入:M×B2维的高斯随机矩阵Φ,原信号x,参数ts=2.8,a=0.8。 输出:重构信号x′。 初始化参数:ε=10-6,n=0。稀疏矩阵ψ采用小波稀疏化,Λ、J、x′为空集。 (1)图像分块:对原信号x按照Z字形扫描得到扫描后的块图像xi,并对块图像xi采用维纳滤波器消除块效应,由yi=Φψxi得到对应yi。 (2)原子初选:计算相关性gi=ΦTri(初选时ri=yi),找出所有满足式(3)的观察矩阵的原子角标值j,存入角标集J中。 (4)弱选择:找出所有满足式(4)的观察矩阵的原子角标值k,存入角标集J中,进入步骤(4)。 (5)更新原子支撑集,即Λ=Λ∪J,合并支撑集得ΦΛ。 (9)整合图像:对输出的重构块图像xi通过逆Z字形扫描整合图像,得到重构信号xi。 以下实验都是通过MATLAB R2009a版本运行,为了验证分段弱选择自适应正交匹配追踪算法的有效性与精确性,采用两种方式对算法进行验证,第一部分采用一维稀疏信号;第二部分采用二维图像信号。 为了验证本文提出算法的可行性,本节针对一维信号进行验证。本节选取随机生成的长度N=256,稀疏度K=20的高斯信号,观测矩阵Φ为M×N的高斯随机矩阵,观测个数M=128。参数设置:SAMP步长L=128,SWAMP阈值ts=2.8,参数a=0.8。 (1)对SWAMP重构精度验证,重构效果如图1所示。 从上述实验可以得出,SWAMP算法能准确恢复原信号且相对误差小。 (2)为了验证SWAMP算法的可行性,本节选取与OMP,SP,ROMP,SAMP同类算法做重构成功概率比较,令K取值0至70,并进行1000次实验,各算法重构效果如图2所示。 图1 SWAMP算法重构效果 图2 同类算法重构成功概率随稀疏度的变化情况 从图2可以看出,随着稀疏度的增加,各个算法重构成功概率呈现降低的趋势。当K<50时SWAMP比OMP,ROMP, SP的重构效果好,与SAMP的重构效果相当,当K>60时,SWAMP才会有较多的信号不能成功重构。 (3)为了验证SWAMP算法的重构效率,本节选取与OMP,SP,ROMP, SAMP同类算法的运行时间比较,令K取值0至40,并进行1000次实验,各算法耗时如图3所示。 图3 同类算法运行时间随稀疏度的变化情况 从图3可以看出,SWAMP算法比OMP与ROMP算法耗时长,与SP耗时相当,比SAMP耗时短,因为SWAMP是双阈值更新支撑集,故通过增加一定时间量换取重构精度。 为了确定SWAMP中阈值ts与参数a,本节选取大小为512×512的二维图像Barbara作为原信号。设定采样率为M/N=0.5,高斯随机矩阵作为观测矩阵,令a=0.8时,阈值分别选取ts=2.6,2.7,2.8,2.9,3。再令ts=2.8时,参数分别选取a=0.6,0.7,0.8,0.9,1。本节采用峰值信噪比PSNR(dB)和算法消耗时间TIME(s)作为客观评价标准,得到仿真实验结果见表1。 表1 不同的阈值和参数对算法重构质量的影响 从表1可以得出,当采样率M/N=0.5时,对于参数a,当a>0.6时重构效果好,并且随着a的增大,运行时间在降低。对于阈值ts,选取不同的阈值重构效果的差异不大,并且随着阈值的增大,重构时间在降低。综合重构的质量与运行时间,当选取参数a=0.8,阈值ts=2.8时,SWAMP算法能平衡重构精度与重构效率,重构质量最高。 对二维图像信号重构,首先对图像进行预处理。利用BCS技术,将512×512的图像分成32×32的块图像,并把块图像拉直作为向量。对每个向量做一维小波变换稀疏化,测量矩阵选取高斯随机矩阵。为了验证本文提出的算法能很好的应用于二维图像信号,本文提出的算法分别对比迭代硬阈值算法(IHT),迭代加权最小二乘法(IRLS),SAMP算法与基于离散余弦变换的平滑投影Landweber重构算法(BCS-SPL-DCT,BSD)。 (1)在同一张图像Barbara上进行重构对比。采样率分别设置为M/N=0.3,0.4,0.5,0.6。参数选择:SAMP步长L=10,BCD块图像大小为32×32,实验结果见表2。 (2)在采样率相同的情况下,比较算法之间对不同图像Lena, Goldhill, Mandrill, Peppers的重构质量,参数设定不变,设置采样率为M/N=0.5。实验结果见表3。 本节采用峰值信噪比PSNR(dB)和运行时间TIME(s)作为客观评价标准。 表2 不同采样率下各算法重构质量比较 表3 采样率M/N=0.5时不同图像重构质量比较 从表2可以得出,随着采样率的增加,各算法的重构质量也越来越好,其运行时间也不断增加。SWAMP在同类算法比较中,重构质量最好。当采样率为0.5时对比各重构算法,SWAMP算法PSNR值相对IHT算法,IRLS算法与SAMP算法分别提高47.48%,12.26%,6.70%。与BSD算法PSNR值相当,但BSD算法通过消耗大量的运行时间换取重构精度,相对BSD算法,本文提出的算法耗时较小。综合得出,本文提出的算法重构质量好,运行效率高。 从表3可以得出,对比在相同采样率下不同图像的重构质量,依然可以看出SWAMP算法对比其他算法有更高的PSNR值,重构质量高,且耗时短,再次验证本文提出的算法有很强的重构能力和很高的运行效率,体现了很好的适用性。 图4中所述几种重构算法都是采用图4(a)作为源图像进行图像重构,得到的重构图像结果如图4所示。图4中得知基于SWAMP重构图像都能较好的对源图像进行图像重构,重构图像整体良好,图像边缘轮廓清晰。比较图4中不同算法的重构结果,本文所述的方法细节纹理特征突出,手臂的轮廓,人物的围巾与裤子等细节纹理都明显优于其他融合算法。其余几种融合方法中,基于IHT的重构图像与基于IRLS的重构图像有明显的噪声,基于SAMP的重构图像整体良好,但细节模糊特别是手臂处呈现锯齿状,基于BSD的重构图像在图像整体与细节方面优于其余3种算法的重构图像,但其耗时长,且在细节纹理上不及本文提出的重构算法。故本文提出的方法能较好对源图像进行重构,且重构图像整体清晰度较高,视觉效果最好。 (1)在图像信号中加入高斯噪声,在含噪环境下,采用不同噪声程度对同一幅图像Barbara使用不同算法进行图像重构。参数选择:SAMP步长L=10,SWAMP参数a=0.8,阈值ts=2.8,设定采样率M/N=0.5,设定噪声是由均值为0,方差分别为σ=0.1,0.01,0.001的高斯噪声,得到的实验结果见表4。 (2)采用相同噪声程度对不同图像Lena, Goldhill, Mandrill, Peppers使用不同算法进行图像重构对比,参数设定不变,设置采样率M/N=0.5,设定噪声是由均值为0,方差为σ=0.001的高斯噪声,得到的实验结果见表5。 本节采用峰值信噪比PSNR(dB)和运行时间TIME(s)作为客观评价标准。 从表4我们得出,当原图像引入高斯噪声时,各算法重构质量下降。当噪声方差扩大时,各算法重构质量下降明显。IRLS算法抗噪性最好,随着噪声方差扩大,PSNR值衰减最小,但运行时间长。本文提出的算法,随着噪声方差的扩大,衰减较明显,但运行时间短,且重构质量也略好于其它算法。综合重构质量与运行效率,本文提出的算法在含噪环境下,仍具有很强的重构能力。从表5中,对比不同图像加入均值为0方差为σ=0.001的高斯噪声,本文提出的算法PSNR值最好,且运行效率高。综合比较不同算法的重构质量与重构效率,本文提出的SWAMP算法具有实用性好,抗噪性强,运行效率高的优势。 图4 不同重构算法图像比较 算法σ=0σ=0.001σ=0.01σ=0.1PSNRTIMEPSNRTIMEPSNRTIMEPSNRTIMEIHT15.73800.6215.58800.5615.04650.5714.07490.55IRLS25.691841.2225.031435.7923.422937.6919.035636.39SAMP27.32242.8625.465410.8421.406810.7414.220712.60BSD29.146873.6327.596473.2021.549855.1714.056245.51SWAMP29.28292.7627.00232.6521.59582.6714.68542.67 表5 对含相同程度的噪声的不同图像重构质量比较 本文在结合现有的压缩感知重构算法,借鉴BCS技术对图像信号进行分块预处理,以提高重构效率,引入StOMP的分段思想,自适应性调节阈值选取初始候选集,采用弱选择标准更新支撑集,提出一种分段弱选择自适应正交匹配追踪算法,该算法可以在稀疏度未知的前提下,实现精确重构。结合对一维信号的重构实验结果表明,相较同类算法,综合重构效率与重构质量本文提出的SWAMP算法优于其他同类算法;结合对图像信号的重构实验结果表明,相较不同算法,本文提出的SWAMP算法相对IHT算法,IRLS算法与SAMP算法PSNR值分别提高47.48%,12.26%,6.70%,PSNR值与BSD算法相当,但SWAMP算法运行时间短,重构效率高;且SWAMP算法具有很强的抗噪性。综合得知,SWAMP算法在重构质量与重构效率上都有很好的效果,具有很强的可靠性与实用性。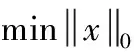

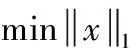
1.2 压缩感知的重构算法
2 分段弱选择自适应正交匹配追踪算法
2.1 对图像信号的预处理
2.2 初始步长选择

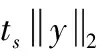
2.3 原子弱选择标准
2.4 算法具体步骤

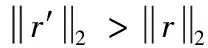
3 仿真结果与分析
3.1 一维信号的重构验证
3.2 参数的选取
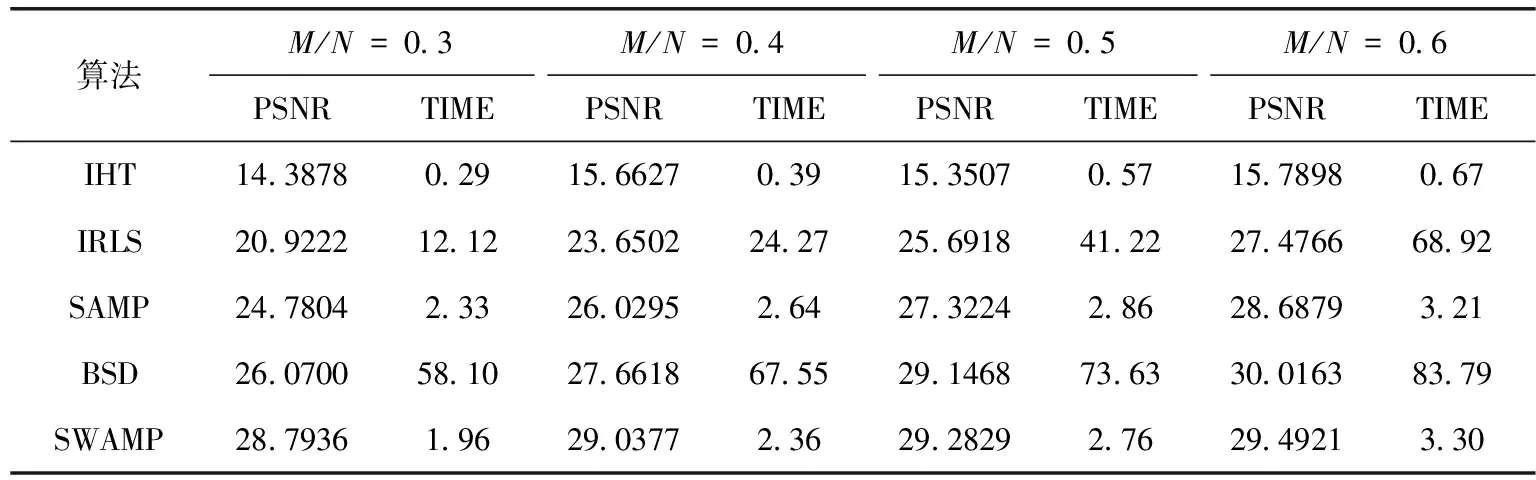
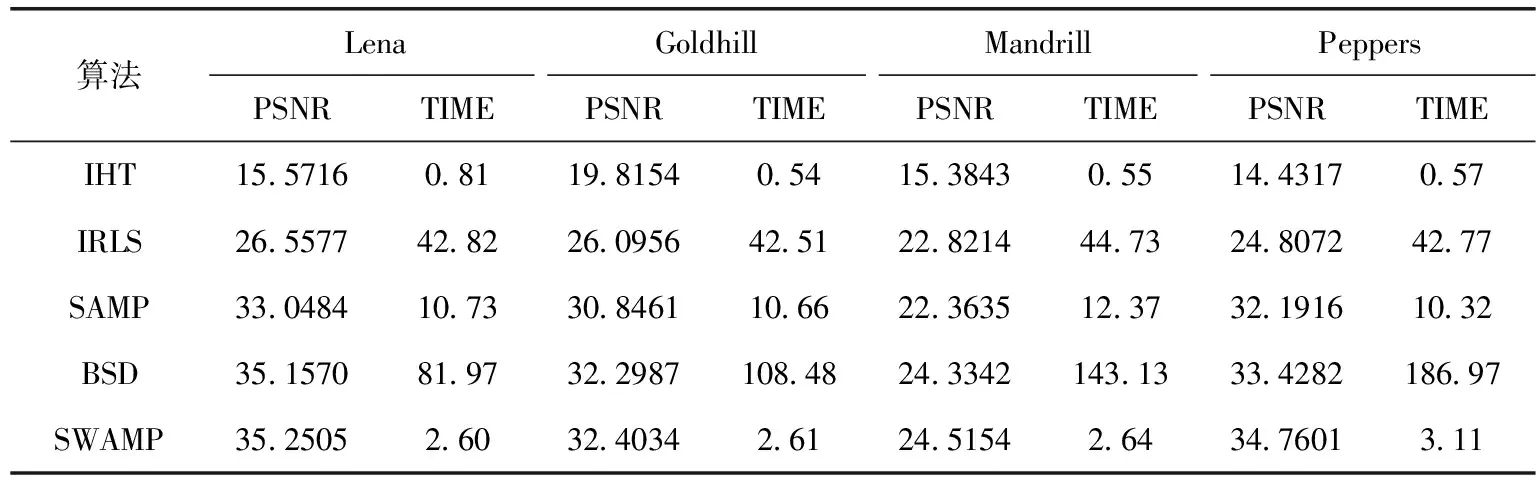
3.3 图像信号的重构
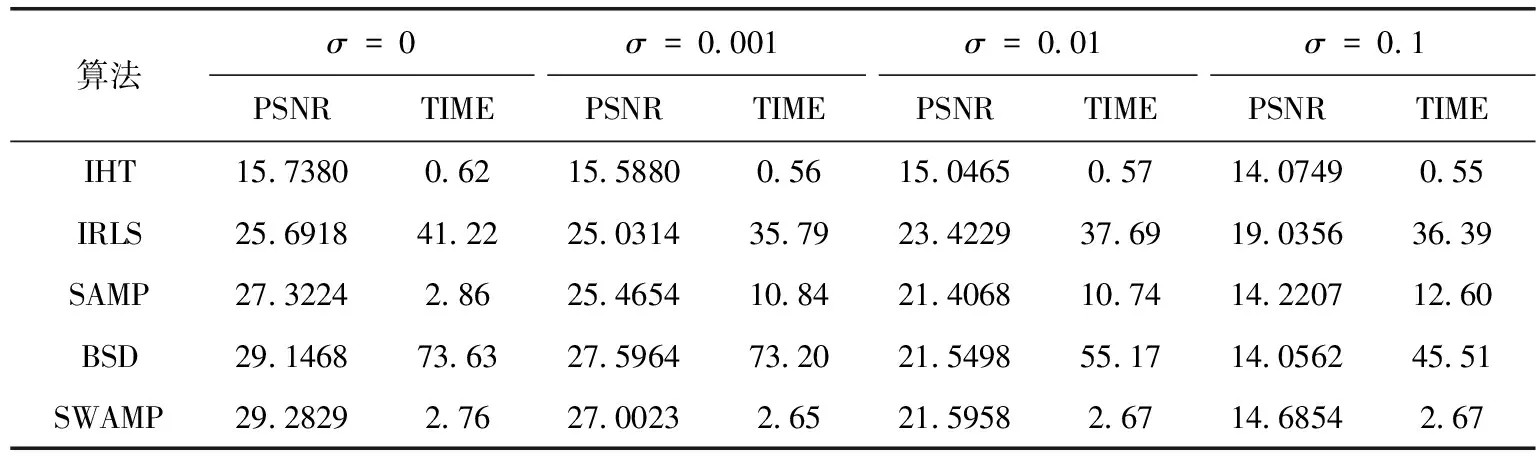
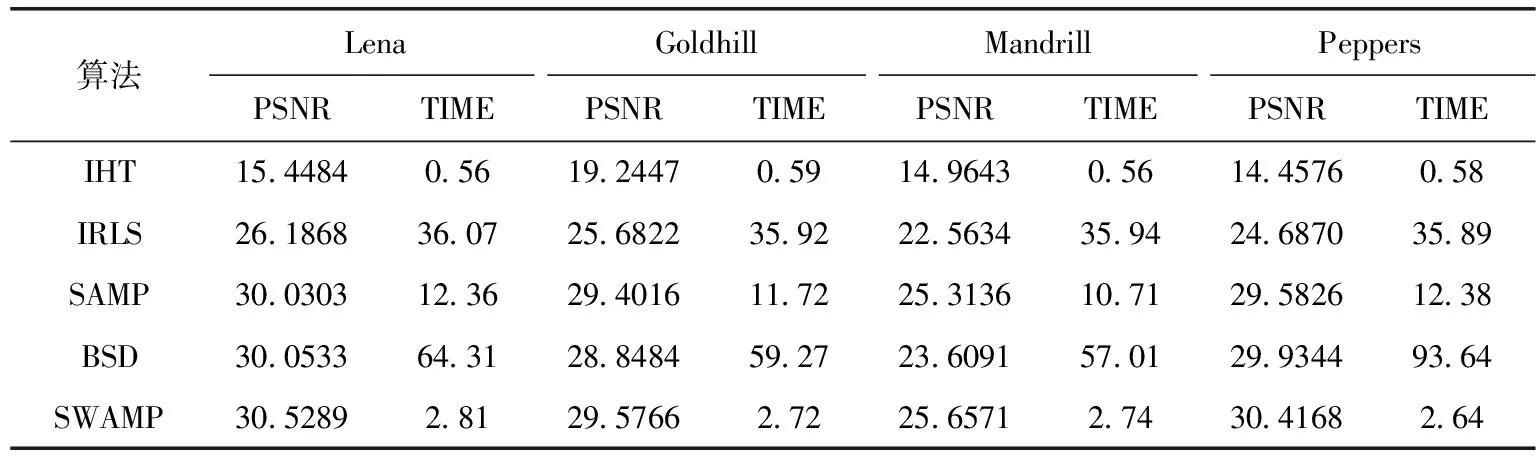
3.4 对含有噪声图像的重构

4 结束语
