加权自学习哈希高维数据最近邻查询算法

熊一利

(江西省教育考试院 信息处，江西 南昌 330038)

0 引 言

所谓的最近邻查询，实际上是给定数据集中返回与查询对象q最为相近的数据对象问题。在数据挖掘[1]、模式识别[2]等多个领域当中最近邻都属于基础研究问题，一般应用时会将其转化成求解近似最近邻问题。在数据增长速度极快且类型越来越多的同时，研究者们都将高效的查询算法与索引结构的设计作为主要研究重点。

学习型哈希[3-8]由于储存与查询方面极为高效，索引在最近邻查询问题中应用非常广泛。大多数学习型哈希法，对于一个给定的查询返回的只是简单的基于海明距离的排序结果。这种计算方法尽管高效，但因为海明距离都是离散取值的，且数据二进制编码长度会给其带来一定的限制，返回结果与查询对象间存在一致的海明距离，但是很难区分不同的二进制编码对象，怎样重新排序候选集中对象是一个非常重要且亟待解决的问题。有关学习型哈希法存在不同二进制编码及相同海明距离的数据无法深入区分的问题，本文通过加权自学习哈希算法的提出有效解决该问题。

1 加权自学习哈希算法

1.1 算法目标

本文提出了一种加权自学习的哈希算法，用于解决高维数据最近邻查找，能够解决不同二进制编码而相同海明距离的数据无法更为深入区分的难题。通过自学习哈希法的应用把原始数据转化成二进制编码，进行学习后获取哈希函数。一旦迎来查询对象后，首要做的就是利用已学习获取的哈希函数转化成二进制编码，接着进行其与各数据的二进制编码之间的海明距离计算，之后回到与特定距离相符的候选集。因为候选集当中有诸多与查询对象编码不同而海明距离相同的数据，实际上与查询对象实际的距离相比这些数据是存在相应差异的，利用海明距离无法进行更为深入的区分。如果去比较原始数据集，那代价比较高昂。为了解决上述问题，我们根据查询对象以及候选集的二进制编码两者具有的特征，赋予二进制变慢不同的权重，最后根据查询对象与候选集的加权海明距离对候选集进行重新排序，使得与查询对象具有相同海明距离不同二进制编码的候选对象能够在更细粒度上进行区分，从而获得更精确的距离度量结果。

1.2 自学习哈希

如图1所示，自学习哈希法实际上包含两个学习阶段，无监督学习为第一个阶段，该阶段主要目的在于把原始空间中的高维数据x转成相对较短的二进制编码y。假设X为数据集合，用m表示，n是数据维度，则数据集的矩阵表示情况如下

自学习哈希通过度量学习方式将xi转化为长度为l比特的二进制编码yi∈{0,1}l，则Y可以表示为n×l的矩阵

有监督学习为第二阶段，把第一阶段获取的所有数据二进制编码yi1,…,yil∈{0,1}视作类标签，通过机器学习法训练出l个分类器，并视作哈希函数h1,h2,…,hl。查询数据x到来时，通过哈希H(x)=(h1(x),h2(x),…,hl(x))将其转化为二进制编码yi1,…,yil∈{0,1}。会将其称作自学习哈希法，主要原因在于其中的数据标签并不是通过人为标注，而是通过学习得到的。

图1 自学习哈希框架

1.3 查询自适应权重

自学习哈希的框架为开放型的，主要包含两个学习步骤，可结合实际的需求以及应用环境明确应使用的方法。和大多数学习型哈希方法一样，自学习哈希仍然存在与查询对象编码不同海明距离相同无法进行更为深入区分的问题。例如q为查询对象，假设其二进制编码为“101”，q与o1(001)、o2(111)的海明距离都是1，但是与q的真实距离是不一样的，通过海明距离无法明确的区分。为使得该问题可得到更好的解决，本文赋予所有的数据二进制编码权重wi，对其加权海明距离进行计算，并重新排序候选集。不同的查询对象得到候选集是不一样的，所以每一次的查询都应当结合不同的候选集对现有的权重向量进行计算，所有将其称作查询自适应权重。

1.4 权重求解原理

假设H(·)=(h1,h2,…,hl)中包含了l个独立存在的哈希函数，由这些函数共同组合而哈希函数向量，H(·)分别把q和o映射成长度为l的二进制编码H(o)和H(q)，而第k比特的二进制编码对应为hk(·)，则q与o的海明距离表示为

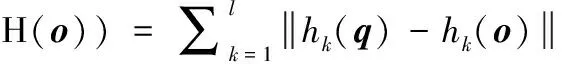
(1)

假设查询对象H(q)各比特的权重为W=(w1,w2,…,wl)，二者的加权海明距离表示为

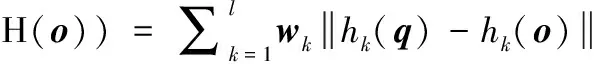
(2)

用p(H(q)=H(o))进行数据对象q和o映射成概率相同的编码的表示，因为每一个哈希函数都是独立存在的，所有相等的两个数据二进制编码与每一个被映射成相同编码概率乘积相同，因此才有

(3)

要想获得每一个比特的权重，就需要借助一个科学的理念，从而促使哈希函数将类似的数据对象处理成比特一样的状态。对于哈希函数而言，可信值提升，对应比特中不同的参数产生了不同的二进制编码，那么同样的概率很小，所相对的加权海明距离则很大。例如，假设q的二进制编码为“101”，o1,o2的二进制编码为“001”，“111”。由左到右，q和o1的二进制编码所处的第一比特部位有差别，q和o2所处的第二比特也有差别。若是第一比特的可信度则比第二比特位更高，可以看出：

q和o2非常接近，同时Dw(H(q),H(o2))w2。

定理1 普通的哈希函数促使相应的数据对象转变为一样的比特，则这个哈希函数的可信值也非常大，其比特的权重也很高。

证明：根据上面的理论，可按照信息熵来验证。此理论中，熵的变化性非常大。很多时候，其中的信息熵越低，指标的变化性越高，其中包含的信息越多。而且综合评估可以实现的效果越大，权重也大，反之亦然。

如果X属于一个离散随即变量，那么其可以在R={x1，x2，…，xn}的范围内取值，这个值是有限的。如果pi=P{X=xi}，那么X的范围则处于xi中。X的熵是这样的

(4)

如果参数q的二进制编码是H(q)，所选择的数据对象位于k比特中，其编码和q一样的机率为pk，不一样的机率是1-pk，选择的数据在正常状态下和搜查参数在对应比特中的编码相同，设置的阈值为pk>1/2，所以有pk>1-pk，第k比特的信息熵为

Ek(H(q))=-pklnpk-(1-pk)ln(1-pk)

(5)

计算出各个指标的信息熵为E1,E2,…,Ek,…,El，通过信息熵计算各比特的权重

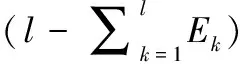
(6)

在信息熵函数中若对数的底取2，则对应熵函数的曲线，当概率pk>1/2时，Ek随着pk的增大而减小。所以有pk越大，Ek越小，wk就越大。

证毕

1.5 求解步骤

以Ck表示查询对象q与候选集结果o在k比特上被映射为相同比特的次数，S(hk(q)=hk(oi))表示hk(q)与hk(oi)是否相等。如果相等，则S(hk(q)=hk(oi))=1，否则为0。于是可以得到

(7)

参数q和所选择的参数的二进制编码中的第k位一样的机率是pk，N代表的是候选集的值，则

pk=C(k)/N

(8)

wk与pk近似单调的线性关系，所有在实际应用中，为了简化计算，可用pk来代替wk。

2 实验验证和结果分析

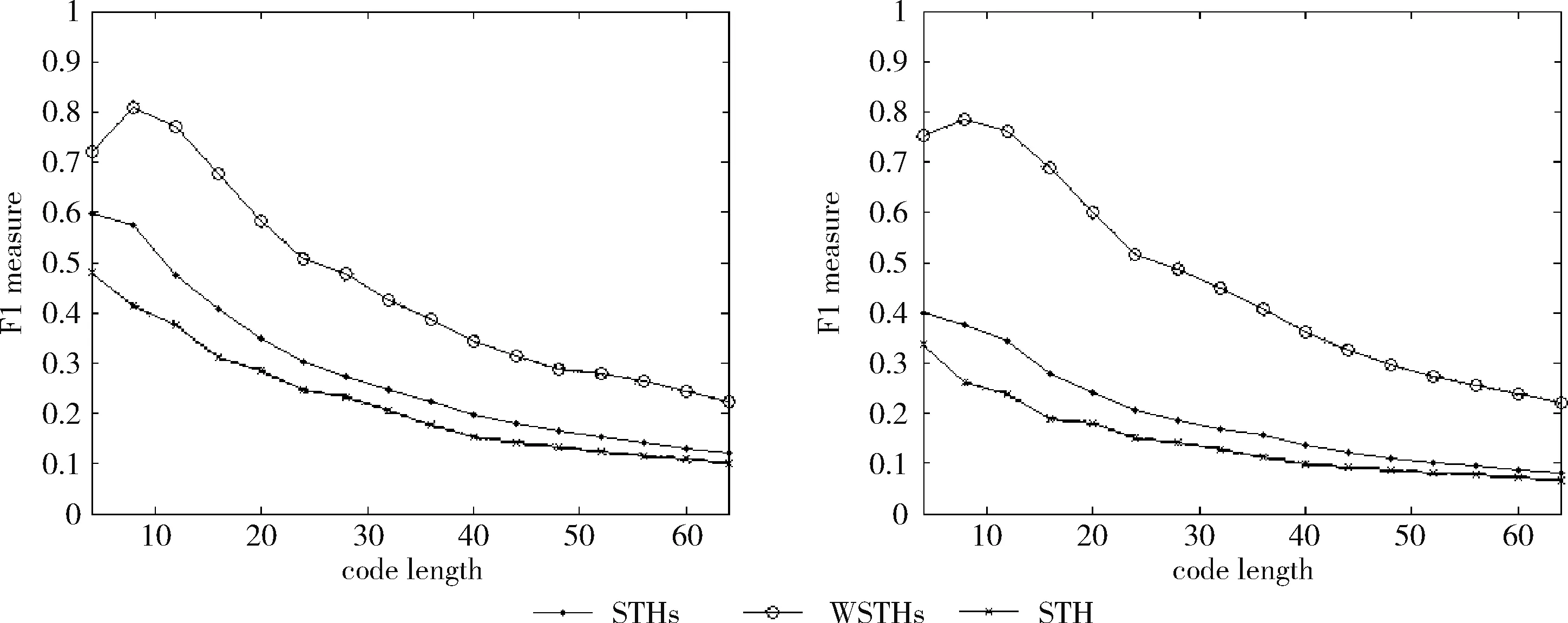
下面将通过实验来验证提出的加权自学习哈希算法在解决最近邻查找问题上的优越性能。在自学习哈希的零监督学习部分，使用拉普拉斯特征映射的方法[9]，促使高维数据映射变成低维实数向量，再借助均值阈值法变成二进制编码。通过拉普拉斯特，能看出参数中的整体结构，同时借助KNN来建立相邻参数的相同矩阵联系，防止因为计算全局相同所以产生时空开销。但在监督学习的过程中，可使用由LIBLINEAR[10]带来的线性SVM，从而对分类器进行划分，获得l个哈希函数。要想更好解决高维数据问题，避免产生非线性可分问题，可以针对SVM中的数据进行设置，借助高斯核函数来取代线性SVM向量内积，另外的数据则恢复默认状态。要辨别一般的STH，便需要在监督学习阶段，借助SVM来进行调整，这种方式被称为是STHs。下面的实验操作中，必须比较STHs与STH的不同。加权自学习哈希(WSTHs)则在STHs基础上由查询所得的候选集计算出二进制编码各位的权重W=(w1,w2,…,wl)，接着计算查询对象与候选集中各个数据的加权海明距离，从而得到更精确有序的结果。并通过实验在3个不同的真实数据集上对比WSTHs和STHs查询性能。

2.1 数据集

笔者针对3个不同的数据集(Reuters21578、TDT2、20Newsgroups)完成操作。在这个过程中，要删除停用词、获取词干，从而完成TF-IDF的核算工作，并且借助稀疏矩阵来进行表达。

20世纪80年代末期，路透社新闻所发表的文章中，结合了所组成的语料库，避免了出现在各种各样的文章中，同时只留下了文章数当中的10个部分，筛选了7300篇不同的文章，训练集涵盖了5225(72%)篇文档，测试集为2057(28%)篇，数据的维度大小为17 024。

TDT2语料库包含了各种不同的文章，这些文章来自新闻节目、报纸文章、电视广播等。除掉来源于各种途径的文章，促使剩下大概30个种类得以保留，获得9421篇文章。在筛选之后，获得训练集的值为5644(60%)篇，测试集为3750(40%)篇，数据的维度大小为33 878。

在语料库20Newsgroups里，大概有19 216篇文章，这些文章来源于不同的类别。按照实际情况来对数据集进行分类，然后获得大小均为12 015(60%)篇的训练集和7532(40%)篇的测试集合，数据的维度大小为25 714。

2.2 评 估

2.2.1 查询结果的F1值

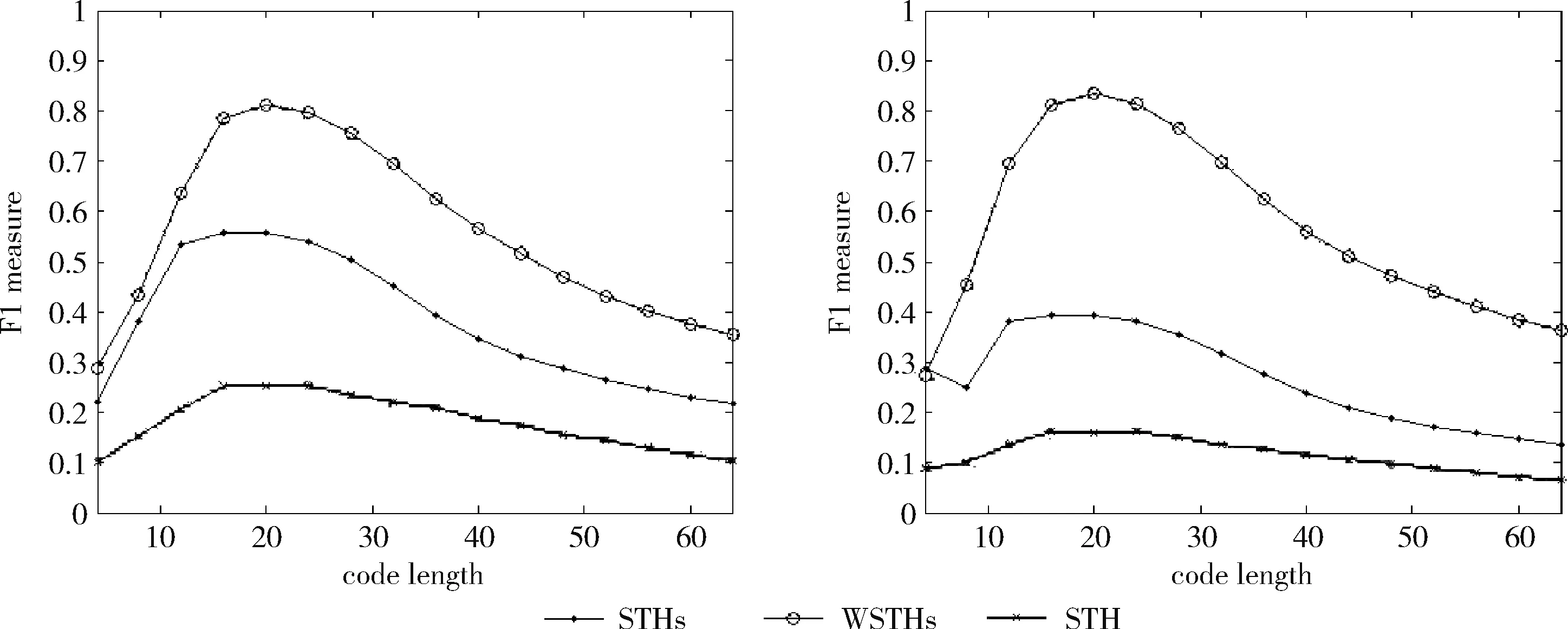
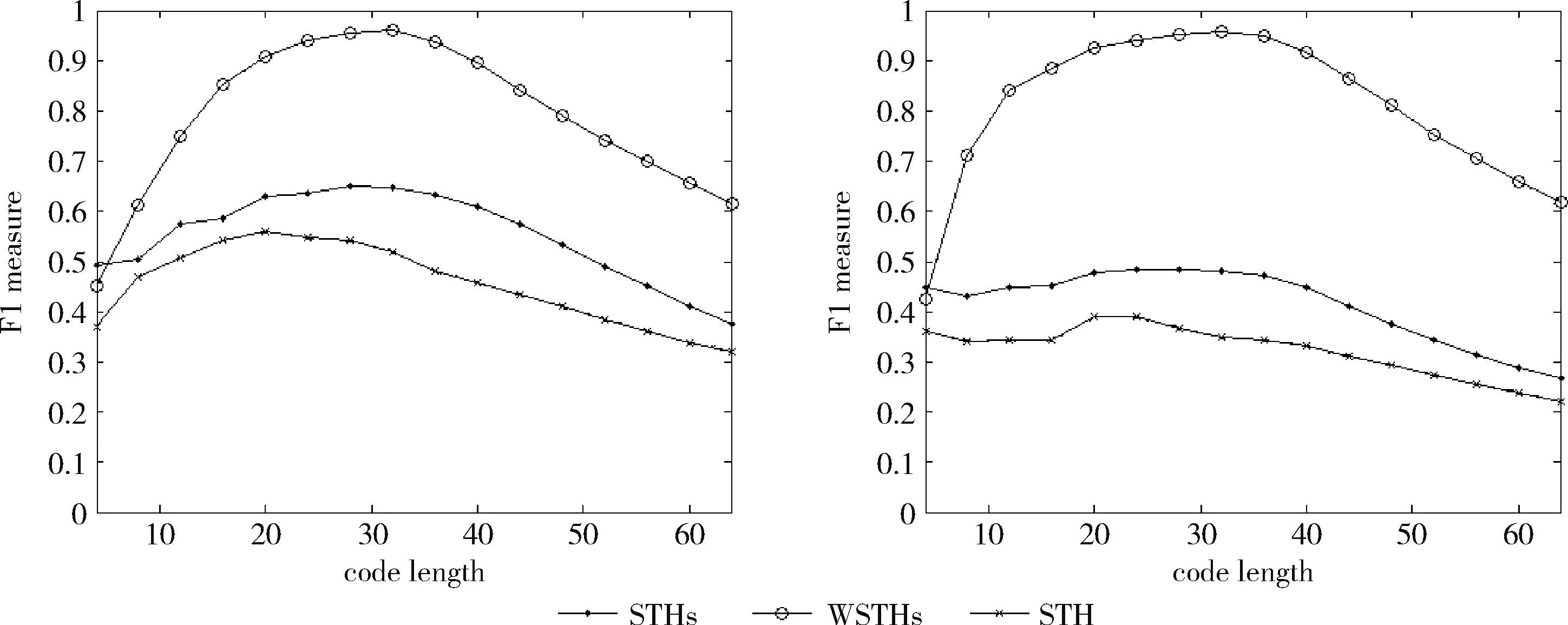
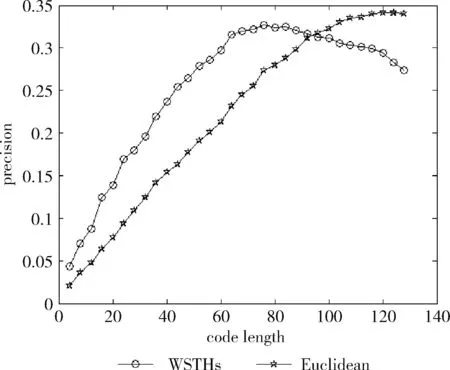
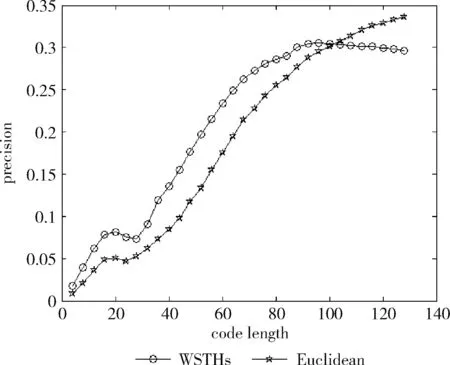
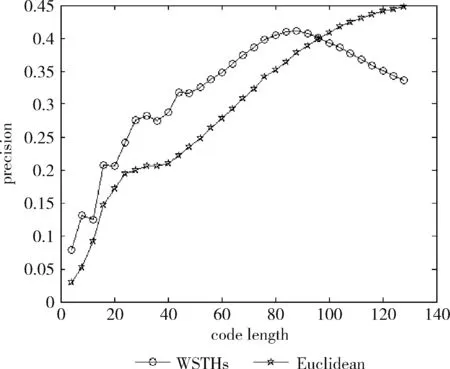
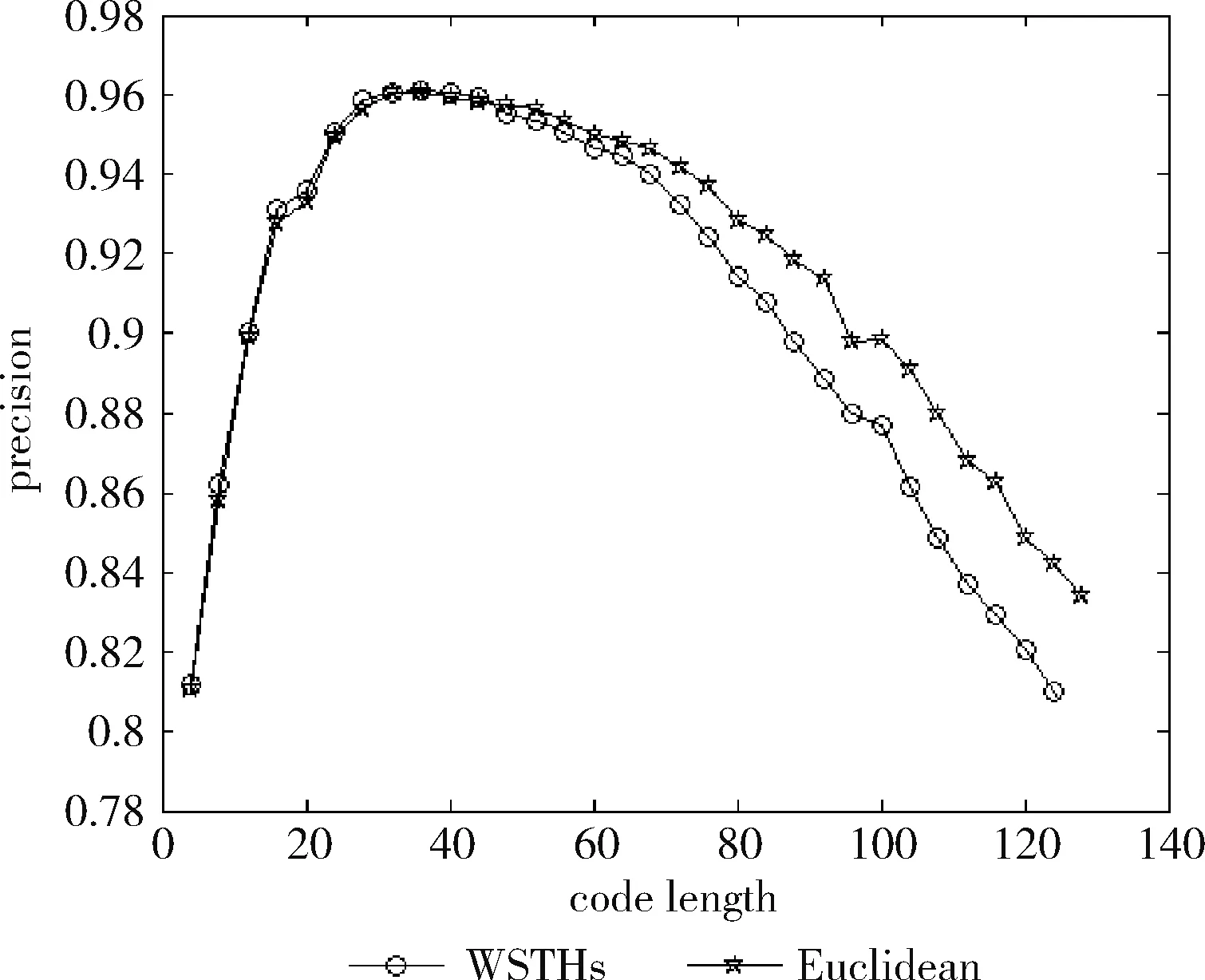
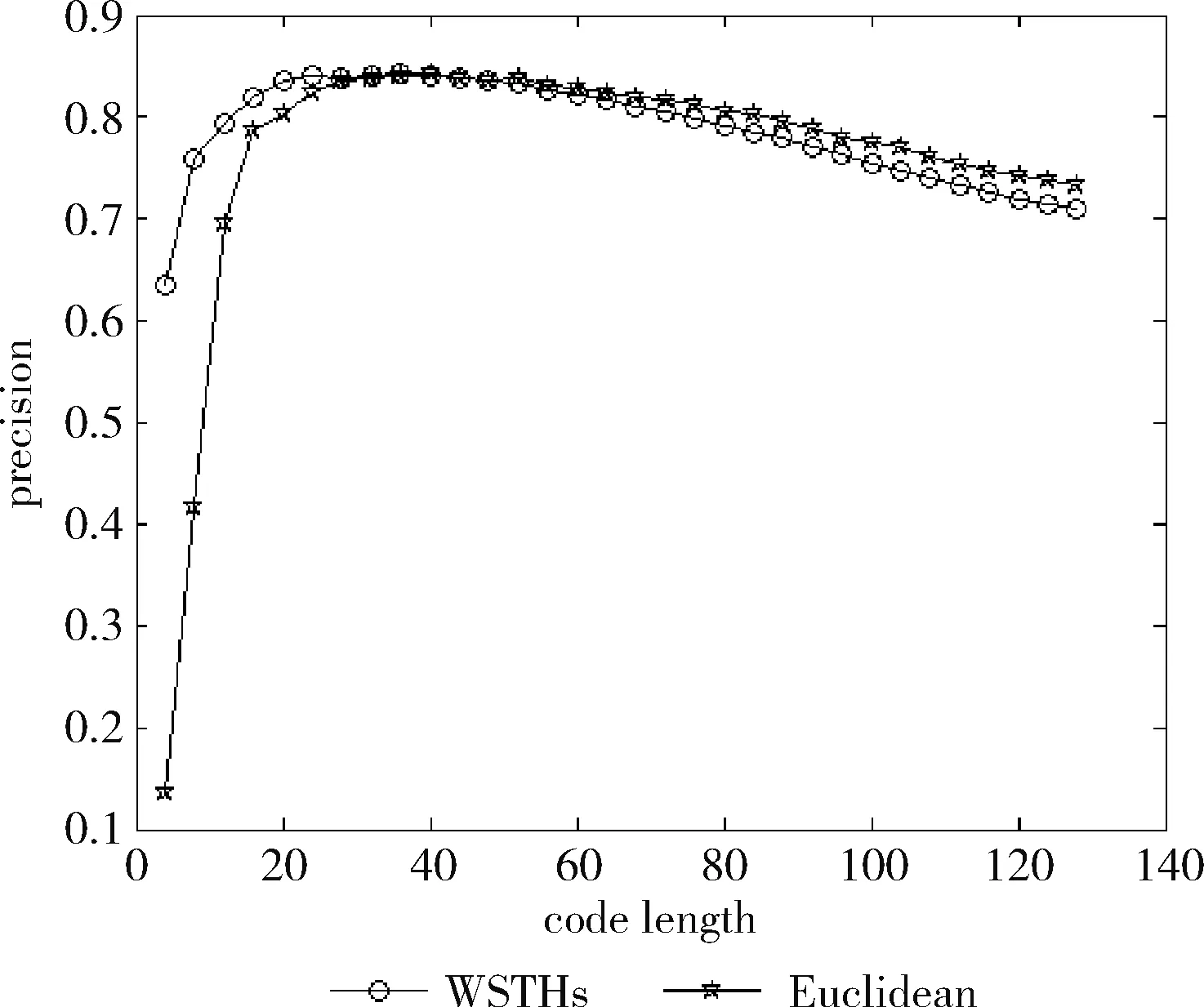
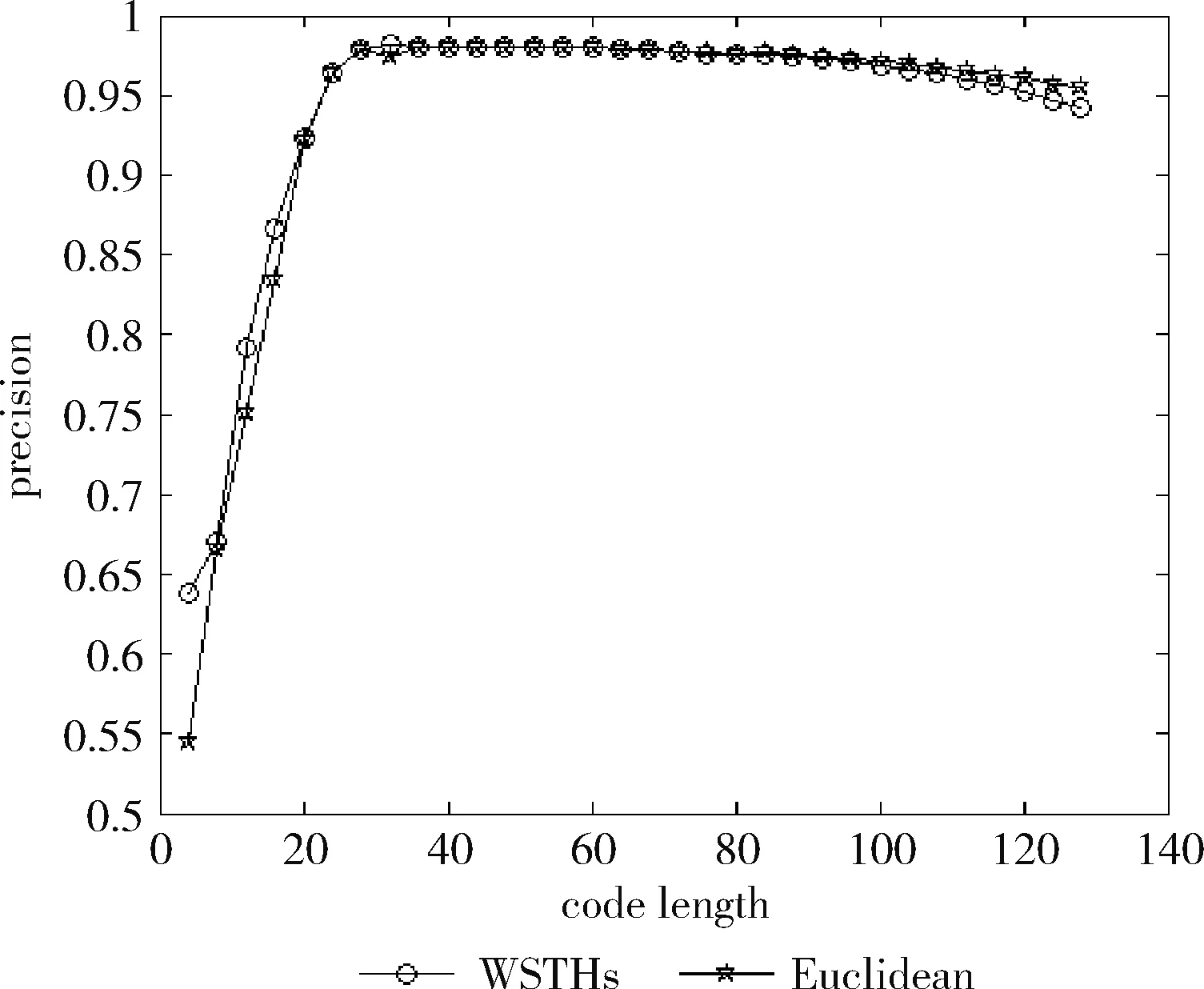
测试数据集中的每篇文档是一个查询数据，根据学习得到的哈希函数将其映射为二进制编码，在训练集中检索满足特定海明距离的对象作为候选集，然后计算权重，根据加权海明距离对这些数据进行重排序。对于不同的相关参数，如果必须返回和海明距离

P=返回结果集中与查询对象是同一类的数量/
返回结果集的大小

(9)

R=返回结果集中与查询对象是同一类的数量/
数据集中与查询对象是同一类的数据数量

(10)

标准的F1值表示为

F1=2P*R/(P+R)

(11)

2.2.2 时间效率

WTHs对STHs进行了优化，在二进制数据中的比特里，添加了各种权重。同时也对无法区别的参数重新排列，该步骤耗费的时间很多。可以采取简易的方法来对候选集进行二次排列，借助对参数的搜索，以及筛选的参数的原始距离，算出这些参数的欧式(Euclidean)距离。对于不同的n维向量a(x11,x12,…,x1n)以及b(x21,x22,…,x2n)，可这样计算

(12)

从上面的公式可以看出，计算欧式距离的时间复杂度为O(n2)。n属于在搜索之后反馈的达到距离要求的候选集的值，k是参数的二进制编码参数。在WTHs算法里，针对候选集二次排序时，会经历这些流程：①按照候选集获得权重，这一部分的实践复杂度为O(nl)；②根据权重计算加权海明距离，这部分的时间复杂度为O(k2)。实验所用的数据集的维度通常很大，二进制编码的长度却很短，所以k≪n。这样一来，在花费的时间方面，WTHs二次排列参数，会比采用计算欧式距离对数据进行排序所消耗的时间更少。

2.3 实验结果

在图2～图4中，横坐标为编码长度，纵坐标为F1值，从上面的实验对比图能够清楚看到，与之前的STH，STHs相比，通过高斯核函数重写SVM后会在一定程度提升F1值，表明了高维数据分类选项高斯核函数的SVM将更为适用。WSTHs相比STHs，F1值有显著提升，前者F1值是后者的1.5～2倍，说明通过加权重排序后，原本难以区分的具有相同海明距离的数据被很好的区分开来，也意味着加权思想的提出是正确的。与此同时，也可得知数据集映以及编码长度不同，也会获取不同的F1值，由如图3～图5得知，在选取8bit、24bit、32bit这3个数据集长度的情况下F1最大，表明了哈希函数学习具有极强的数据依赖性。数据集不同的情况下分布也会不同，各个数据维度也会具有不同的重要性，且利用加权算法得到更为精确的返回结果。纵观实验结果可知，并非是有更长的编码就意味着更好，主要由于在于有越长的编码，则与查询对象具有相同海明距离的不同编码的可能情况就越多，比特的权重被稀释，变得难以区分。而编码的长度太短时，数据量越大，则不同的数据的二进制编码相同的概率越大，使得查找的准确率降低。

图2 Reuters21578上F1值随编码长度变化曲线(左图N1=N/2,右图N1=N/3)

图3 20Newsgroups上F1值随编码长度变化曲线(左图N1=N/2,右图N1=N/3)

图4 TDT2上F1值随编码长度变化曲线(左图N1=N/2,右图N1=N/3)

从上文中进行的分析时间效率理论得知，WTHs重新排序候选集耗费的时间要比原始数据Euclidean距离直接计算耗费的时间短很多，下文中将利用实验进行验证，详情见表1。

表1 对比WTHs与直接计算Euclidean距离所耗费的时间/s

从上面的实验数据可以看出，通过WTHs算法对候选集进行重新排序耗费的时间要比欧式距离计算耗费的时间短很多，后者将为前者10至20倍的时间耗费。而时间响应要求较高的应用，必然是要优先选择WTHs。

此外，对于一个好的算法，需要权衡各方面的因素，除了时间效率外还需考虑空间效率和算法的准确性。空间上，由于WTHs算法将数据转化为了一串较短的二进制编码，所有空间效率也大大提高。为了对准确性方面WTHs以及欧式距离直接计算的表现进行对比，任何一次查询都应当将两种算法排序后前N/2个数据作为最终的返回结果，根据前面准确率的公式可知，返回结果集中与查询对象属于同一类的数据对象越多则查询的准确率越高实验结果如图5～图7所示。

图5 Reuters21578上准确率对比

图6 20Newsgroups上准确率对比

图7 TDT2上准确率对比

从上面3个数据集合上的实验对比可以看出，当学习数据的二进制编码长度小于96 bit时，WTHs与直接计算Euclidean距离两种算法的对比可知，前者在数据排序查询方面具有更高的准确率。主要原因为欧式距离采用相同的方式对待数据的各维度，而WTHs采用不同的方式，其更可凸显数据不同维度重要性差异。当数据的二进制编码大于96 bit时，直接计算欧式距离的准确率要高于WTHs算法。显然，学习型哈希的优势在能够用较短的二进制编码来表示数据，并且能够提高查询的准确性。

除了进行WTHs和直接计算Euclidean距离两者在数据排序查询方面的准确率对比，这两种方式在KNN分类方面的准确性我们也进行了相应的对比。KNN是通过返回的数据集来推测查询对象的归类，有更高的准确率，就意味着取得的k近邻与其越相似。下面是WTHs和直接计算Euclidean距离时KNN分类准确性实验对比结果，假设N为每次查询返回的满足距离要求的候选集的大小，k取N/2。

从图8～图10可以看出通过WTHs所得结果集来进行KNN分类的准确性与直接计算Euclidean距离在编码长度小于60 bit时并没有下降，在某些情况下反而有所提高，这也从侧面说明了与传统Euclidean距离计算相比，WTHs在时间方面的优势极强，同时准确性方面也得到了保证。

图8 Reuters21578上KNN分类准确性

图9 20Newsgroups上KNN分类准确性

图10 TDT2上KNN分类准确性

3 结束语

大部分学习型哈希法把原始空间的高维数据映射到海明空间的低维数据后，因为量化与降维两个步骤会造成一定的损失，导致海明距离一致的数据对象与查询对象无法进行更为深入的区分。而不同的数据维度，也会相应的携带不同的信息，而相对应的转化之后的二进制编码也会具有不同的重要型。为使得返回结果更加准确，在自学习哈希架构基础之上，依据查询对象与候选集相同比特的统计特征对比特赋予不同的权重，最后将加权排序结果返回。本文从理论分析入手，并采用实验的方式对加权自学习哈希方法的高效性以及准确性进行验证。