改进BP神经网络在机票销售量预测中的应用
2018-12-22罗嗣卿李冰珂王佳玉
罗嗣卿,李冰珂,王佳玉
(东北林业大学 信息与计算机工程学院,黑龙江 哈尔滨 150040)
0 引 言
寻找稳定、精确的销售量预测模型一直是国内外研究者关注的焦点,并且具有重要的意义。BP神经网络是常用的预测算法,传统的BP神经网络是通过梯度下降法[1]进行学习,随机生成权值和阈值,如果这两个初始参数选择不当,网络就会出现局部最优或收敛速度慢等问题,对此很多学者提出利用智能算法来优化网络的权值和阈值[1],比如布谷鸟搜索算法[2,3]、萤火虫算法[4]、遗传算法[5-7]等。为了更好地改善BP神经网络存在的问题,本文提出用改进的和声算法来优化BP神经网络。和声算法是一种新的启发式优化算法[8],为了有效提高和声算法性能,许多研究人员通过自适应参数[9]、动态调整[10]、智能调整(ITHS)[11]、混沌和声[12]、引入变邻域搜索[13]、差分进化算法[14]等方法优化HS算法[15],在前人研究的基础上,为了使和声算法能够更大程度上优化BP神经网络,提出自适应和声算法与遗传算法的混合算法(GA_HS)来优化BP神经网络的权值和阈值[16],能够很好地改善了BP神经网络的易陷入局部最优、收敛速度慢等缺点。最后,将GA_HS算法应用到机票销售量预测问题中,建立对比模型完成实验,检验本文提出的算法模型预测效果。
1 传统BP神经网络
BP神经网络是一种多层前馈网络。网络模型的拓扑结构包括输入层、隐含层和输出层。其中,三层网络结构如图1所示。

图1 BP神经网络结构
传统BP神经网络通过训练误差反向传播算法进行训练,包括正向传播和反向传播两个过程。下面具体介绍这两个过程:
步骤1 正向传递子过程。设节点i和节点j之间的权值为wij,节点j的阈值为bj,xj为节点的输出值,将其代入激活函数得到每个节点的输出值。具体计算方法如下
(1)
xj=f(sj)
(2)
其中,f为激活函数。
步骤2 反向传递子过程。沿正向传播的反方向调节各个神经元的权值和阈值,最终达到期望值和预测值误差最小。假设输出层的所有结果为dj,误差函数如下

(3)
由梯度下降法可知,权值的修正值与E(w,b)的梯度成正比,那么对于第j个输出节点有

(4)
若选择激活函数为
(5)
那么隐含层与输出层之间的权值和阈值需要做如下调整

(6)
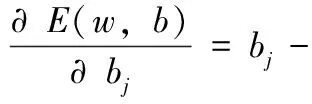
(7)
同理按照上述方法调整输入层和隐含层之间的权值和阈值。
以上是BP神经网络全过程。网络对初始参数值有较高要求,所以容易形成局部最优而得不到全局最优值。
2 传统的和声算法
和声算法是一种新颖的启发式全局搜索算法。由N个人组成一个乐队,每个人演奏一种乐器,他们演奏加起来对应一组和声,乐队通过不断排练得到最好和声效果的过程中使用一个f(x)函数来衡量和声的效果好坏,没有得到满意的和声之前一直演奏,直到达到要求,这就是和声算法的最优化过程。具体算法步骤如下:
步骤1 确定初始化和声算法的基本参数、所需优化问题的目标函数以及约束条件。其中参数包括和声库大小(HM)、记忆库取值概率(HMCR)、微调概率(PAR)、音调微调带宽(bw)、创作的次数(Tmax)。
步骤2 确定解空间。有N个乐器,每个乐器都有一个确定的音乐演奏范围,通过该范围确定一个解空间。
步骤3 初始化和声记忆库。和声记忆库是根据解空间和初始化的和声库大小随机产生。
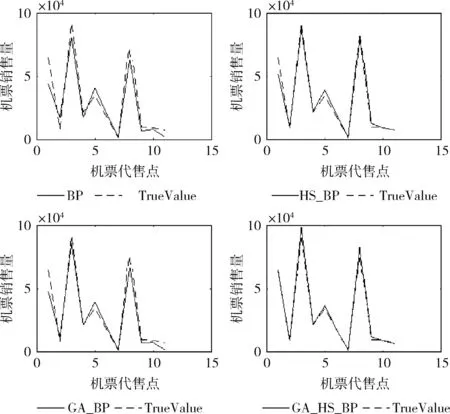
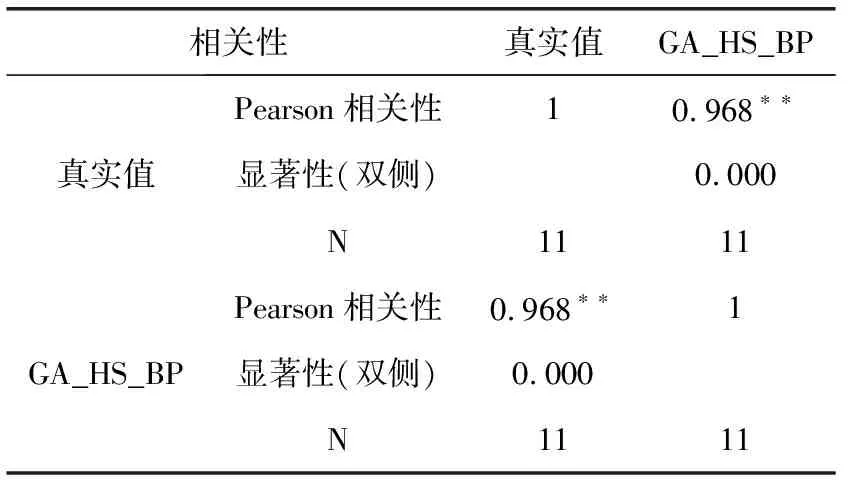
步骤4 产生一个新和声。随机产生一个变量rand1(rand1∈[0,1])。并将rand1与初始化的HMCR进行比较。若rand1>HMCR,从解空间中随机选取一组和声;rand1 步骤5 更新和声库。比较目标函数值f(x),如果新和声优于初始化和声库HM中的最差解,那么和声库中最差的和声将被新和声替换掉。 步骤6 重复上面两步过程,直到达到创作次数最大值。 遗传算法是一种通过模拟自然进化过程来搜索最优解的方法,该算法在产生初始种群之后,按照适者生存和优胜略汰的原理,根据具体问题的适应度值大小选择较优个体,并仿照遗传学方法设置遗传算子,然后完成对个体交叉和变异操作,更新种群。 本文提出的自适应和声算法与遗传算法的混合算法(GA_HS),具体思想是先对HS算法进行改进,使微调概率(PAR)和音调微调带宽(bw)具有自适应性,并在更新和声种群过程中引入交叉、变异操作。然后利用GA_HS算法优化BP神经网络权值和阈值,这样不仅减小了网络的训练误差、也避免了网络陷入局部最优。具体优化操作如下: (1)对HS算法中的PAR、bw参数作自适应调整。HS算法的初始参数设置十分重要,如果选择不当则严重影响着算法搜索性能。传统的HS算法初始化参数过程是将PAR、bw等参数设置为固定值,而GA_HS算法解决了参数选择不当给搜索过程带来的误差过大、收敛速度慢等问题。GA_HS算法首先给bw和PAR设置一个较小的初始值,然后每次迭代根据适应度值的大小(也就是BP神经网络的误差值)反复调整这两个参数,最终使适应度值达到最小,具体运算步骤如下 f是适应度值,bw0为bw的初始值,PAR0为PAR初始值。 (2)GA_HS算法在传统的HS算法基础上做出改进。传统和声算法每次迭代是一次产生新和声更新和声库的过程,该过程只对原和声库进行了很小程度的更新,发现更优种群的速度较慢并且容易陷入局部最优,而遗传算法中所使用的交叉和变异操作可以解决这一问题。本文提出的GA_HS算法,首先设置一定的交叉概率和变异概率,然后在每次更新种群的迭代过程中,增加遗传算法的交叉、变异操作,使得算法更快找到更优种群,不仅能够保证了种群的多样性,还可以防止算法陷入局部最优和过早收敛。主要操作如下: 交叉操作: 其中,pc为交叉概率,pm为变异概率。 (3)传统BP神经网络随机生成权值和阈值,然后利用梯度下降法调整这两个参数,因此它具有陷入局部最优、收敛速度慢等缺点,本文首先采用GA_HS算法对网络权值和阈值进行优化,优化BP神经网络的过程中适应度函数的选取十分重要,由于训练网络的每次迭代过程都是通过训练样本误差值大小来反复修改网络的权值和阈值,所以本文提出的GA_HS算法选取BP神经网络的误差函数作为适应度函数,通过反复迭代使得适应度函数值达到最小,也就使得训练样本的误差值最小,从而得到最优的初始权值和阈值,达到优化BP神经网络的目的。其次在建立模型时隐含层节点数设置和训练函数的选取两方面也做了一定的改进,解决了传统BP神经网络所存在的问题,使其有更好的预测效果。 GA_HS算法优化BP神经网络流程如图2所示。 BP神经网络是目前应用十分广泛的一种网络模型。为了验证本文优化方法的有效性,提取某城市的11个机票代售点的200天的销售量为实验数据,选取前185天的机票销售量为训练样本,最后15天为测试样本,利用测试样本中的前14天数据来预测最后一天的机票销售量,对GA_HS算法、GA算法、HS算法优化BP神经网络以及传统BP神经网络分别建立模型,然后得出4种模型的预测值与真实值最终对比结果。实验模型采用单隐含层网络结构,设置11个输入层节点,11个输出层节点。另外,隐含层节点个数对网络的性能有很大影响,节点数太少,则在预测过程中难以保证效果的准确性,节点数太多,则在网络训练过程会导致训练时间太长,预测效果不准确等问题。本文首先利用经验公式确定隐含层节点数范围,再将该范围内所有整数值代入实验模型进行适应度值对比,通过实验对比可知当选取10个隐含层节点时,样本均方误差值最小。因此,模型设置10个隐含层节点数。经验公式为 (8) 其中,h、m、n分别为隐含层、输入层、输出层节点数,a为1~10之间的常数。 传递函数和训练函数的选择也关系着模型的性能,因此选择logsig、tansig函数分别作为输入层和隐含层之间、隐含层和输出层之间的传递函数。选取trainlm函数为训练函数,该函数采用的训练方法是一种介于牛顿法和梯度下降法之间的非线性优化方法,它对冗余参数问题也能很好的处理,减小了代价函数陷入局部极小值的机会。当λ很大时,它的步长接近牛顿法步长,当λ很大时,它的步长接近梯度下降法步长。因此,本文为了模型能够达到更好的效果,选取trainlm函数作为训练函数。 传统和声算法参数设置主要包括以下几个,其中和声库大小为20,迭代次数为100,HMCR为0.75,PAR和bw设置为0.2。GA_HS算法设置PAR和bw初始值为0.02,交叉概率pc为0.75,变异概率pm为0.25。 模型的最终输出结果为所有代售点最后一天的机票销售量预测值,再与最后一天的真实值进行对比,得出实验结果。分别建立传统BP网络(BP)、和声算法优化BP网络(HS_BP)、遗传算法优化BP网络(GA_BP)、遗传算法和自适应和声算法的混合算法优化BP网络(GA_HS_BP)4种模型,用matlab编程语言编码完成对比实验。 图2 GA_HS_BP算法流程 在图3中,通过3种GA、HS、GA_HS算法的适应度值对比可知,遗传算法的误差较大。对比HS算法和GA_HS算法,GA_HS算法先将PAR和bw设置为一个较小的初始值,随着不断迭代寻找更优种群,初始参数也不断进行自适应,得到更小适应度值,因此当迭代次数较少时,GA_HS算法比HS算法适应度值大,但是随着迭代次数增加,改进的和声搜索算法逐渐找到接近最优种群的较优种群,使得适应度值突然减小,当迭代次数超过90次后,适应度值达到很小,预测值更加逼近真实值。 图3 GA、HS与GA_HS算法适应度值对比 由表1对比结果可以看出,BP、GA_HS、HS_BP、GA_HS_BP这4种模型的均方根误差值依次减小。本文提出的GA_HS算法得到的均方根误差最小,因此它对机票销售量的预测具有更高的准确度。 表1 均方根误差对比结果 在图4中,可以看出GA_HS算法优化BP神经网络实验最终得到的预测值与期望值的折线图几乎完全重合,但是由于销售代理点的销售量达到了上万级,预测值与真实值的差值远远小于销售量数值,所以通过图4不能很直观的表现出BP、GA_HS、HS_BP、GA_HS_BP这4种模型预测值与真实值对比的好坏程度。因此,通过spss软件对4个模型的预测值和真实值作相关性分析。如表2~表5所示,可以直观的看出,BP、GA_HS、HS_BP、GA_HS_BP这4种模型与真实值的相关性依次增大,其中GA_HS_BP模型预测结果最接近真实值。由此可知,本文提出的GA_HS算法优化的BP神经网络预测更为准确。 图4 4种模型预测值与真实值对比 相关性真实值BP真实值Pearson相关性10.733∗∗显著性(双侧)0.000N1111BPPearson相关性0.733∗∗1显著性(双侧)0.000N1111 注:**.在.01水平(双侧)上显著相关。 表3 GA_BP模型预测值与真实值相关性分析 注:**.在.01水平(双侧)上显著相关。 表4 HS_BP模型预测值与真实值相关性分析 注:**.在.01水平(双侧)上显著相关。 表5 GA_HS_BP模型预测值与真实值相关性分析 注:**.在.01水平(双侧)上显著相关。 本文利用自适应和声算法和遗传算法的混合算法(GA_HS)改进的BP神经网络完成对机票销售量的预测。由上面的仿真预测结果可知,GA_HS_BP模型明显优于GA_BP模型、HS_BP模型、BP模型的实验结果。但本文只是对于BP神经网络的权值和阈值这一方面进行了优化,其它方面也有很大的优化空间,其它研究人员也可以提出更好的方法来优化它的权值、阈值或者对其它角度优化进一步提高预测准确率。3 改进的和声算法优化BP神经网络


4 模型的建立以及预测结果分析
4.1 模型建立

4.2 实验结果分析





5 结束语
