基于改进RRT算法的四旋翼无人机航迹规划
2018-12-22成浩浩齐晓慧
成浩浩,杨 森,齐晓慧
(陆军工程大学石家庄校区 无人机工程系,河北 石家庄 050003)
0 引 言
由于低空飞行环境复杂,四旋翼无人机飞行时常受到障碍物的影响,当飞行航线上突然出现障碍物时,其要具备对飞行路线进行重规划的能力[1]。在航迹规划方面很多学者提出了不同的算法,如人工势场法[2,3]、A*算法[4,5]、概率路线图法(probabilistic roadmap method,PRM)[6]、蚁群算法[7]、遗传算法[8-10]等。RRT算法是S.M.LaValle[11]提出来的基于采样的增量式搜索[12]算法。该算法不需要建立空间信息模型,以随机采样的方式在任务空间中均匀采样,因此具有概率完备性,相较其它算法更适合高维空间中的四旋翼无人机航迹规划研究。
然而,RRT算法存在全局随机搜索,运算量大,实时性较差,航迹由随机点组成,通常不是最优航迹[13],规划航迹不平滑的缺点。为此,不少学者进行了改进:针对RRT算法随机搜索、实时性较差的缺点提出了引导策略,针对路径不平滑的特点提出动态步长策略或者航平滑优化策略。这些改进方法大都是单一的,效果受到了一定程度的影响。本文从3个方面综合考虑,提出了3种优化策略:启发式搜索策略、动态步长策略和双层平滑度优化策略,并将其应用于四旋翼无人机两种类型的动态航迹规划中,在二维和三维环境下进行仿真分析,检验这种综合改进型算法实时性和航迹平滑度等性能。
1 传统RRT算法简介
RRT算法包括随机树的生长和航迹反向搜索两个阶段。在随机树生长阶段,以出发点Pstart为树的根节点,在任务空间随机生成一个随机点Prand,找出树中与随机点Prand最近的叶节点Pnear,然后从Pnear出发,在与Prand的连线上选择一个步长ε找到点Pnew,检查Pnew是否在障碍物区域内,Pnear与Pnew的连线上是否有障碍,如果有,则重新选择随机点Prand,否则将Pnew接入树中形成新的叶节点,随机树不断生长,直到叶节点到达目标点或者到目标点的距离小于一个设定的范围,随机树生长过程结束;在航迹反向搜索阶段,形成从目标点到出发点的贯通航迹,规划结束。随机树的生长过程如图1所示。

图1 随机树生长过程
传统RRT算法遍历搜索所有空间,不会存在规划失败的情况,但是这种随机的遍历搜索会使随机树节点产生大量的冗余,算法实时性降低,规划航迹曲折。
鉴于RRT算法实现分为随机树生长的引导和规划航迹的平滑优化两个阶段,本文从引导策略、步长选择、航迹优化方法3个方面进行综合考虑。
2 综合改进的RRT算法
传统RRT算法在随机树生长过程中会出现很多的冗余,浪费了规划时间,降低算法的实时性,并且生成的航迹较曲折,导致航迹的跟随性降低。如果引进基于概率引导的启发式搜索策略,指引随机树朝目标点的方向生长,将会在一定程度地减少规划时间,提高算法实时性;动态步长策略,侧重于解决算法实时性和平滑度之间的矛盾,即提高算法实时性又使规划的航迹尽量平滑;而双层平滑度优化策略的引入,则对航迹的平滑度进行优化,规划出从起始点到目标点的较优路径。
综合改进RRT算法流程如图2所示:首先,利用启发式搜索策略进行空间搜索,找到下一个待扩展的叶节点;然后利用动态步长策略实现随机树扩展生长;最后找到可行航迹后通过双层平滑优化策略进行航迹平滑优化,规划出适合四旋翼无人机飞行的可行航迹。

图2 综合改进RRT算法流程
2.1 基于概率引导的启发式搜索策略
传统RRT算法在任务空间随机产生Prand,这虽然有利于算法探索未知区域,但是搜索的点会产生很多冗余,增加算法运行时间,降低算法实时性。文献[12]提出了双层启发式优化策略,即面向目标的启发式搜索策略和面向可跟踪性的航迹平滑优化策略。在面向目标的启发式搜索策略中,提出了启发式采样策略和新节点启发式扩展策略。面向目标的启发式采样策略是在随机点的选取上,让其以一定的概率θ(0<θ<1)选目标点为随机点;新节点启发式扩展策略是在新节点的选取上,让新节点生成的方向以一定的概率τ(0<τ<1)设定为目标点方向。这种优化策略在障碍物较少时可以增强随机树向目标点生长的趋势,使搜索更具有指向性,减少大量的冗余节点,增强算法实时性。但是在障碍物较多时,这种优化策略由于丧失了部分选择性,反而导致搜索效率较低;同时两步的优化会耗费更多的时间。为此本文借鉴了面向目标的启发式采样策略,提出了基于概率引导的启发式搜索策略,不对新节点的选取进行引导,通过调整θ来达到指向目标的目的。这种改进在不失算法指向性的前提下,可以提高算法的收敛速度,为后面的航迹平滑度优化节省出一定的时间。
2.2 动态步长策略
传统的RRT算法步长是固定的,当选用大步长时,算法能够很快地收敛到目标点,但是航迹平滑度很差;当选用小步长时,航迹的平滑度得到改善但是却是以牺牲算法实时性为代价的。为了解决算法实时性与平滑度之间的矛盾,文献[14]提出了动态步长策略,加入了目标引力思想,新节点的计算公式如下
(1)
其中,ρ1是随机点方向步长,ρ2是目标点方向步长。通过调整ρ1和ρ2的权值达到改变步长的目的。这种动态步长的优化达到了在障碍物密集区域改变步长的目的,并且可以使新节点朝着目标点方向生长。但是到达阈值后ρ1和ρ2的权值固定,不能随着与障碍物距离的远近而变化。
受文献[14]的启示,本文提出了新的动态步长策略,步长选取函数为
εnew=(keαd-0.8)·ε
(2)
其中,ε是原始步长,εnew是障碍物附近的步长,d是算法叶节点当前位置与障碍物之间的距离,α是衰减系数,k是调节因子,α和k的取值与阈值的选取有关,要确保到达阈值时εnew≤ε。
新动态步长策略的思想是:在随机树离障碍物较远、没有到达阈值时采用原先步长ε,加快算法收敛速度;随机树生长到障碍物附近、达到阈值时采用小步长εnew,确保航迹平滑度。这种改进虽然不能使新节点朝着目标点选取,但是可以使步长随着障碍物之间的距离而变化,更好地解决实时性与平滑度之间的矛盾。算法的指向性可以通过调整第一种改进策略中θ的值来弥补。
2.3 双层平滑度优化策略
传统RRT规划完航迹之后存在的最大的问题就是航迹平滑度的问题,为了改善航迹平滑度,文献[15]提出了一种平滑度优化策略:先对图3中转折角大于120°的相邻路径进行删减平滑,然后采用三次贝塞尔曲线进行优化。这种优化方法优化后的航迹都是曲线,非常平滑,但是这种三次贝塞尔优化增加了路径中节点的数量,考虑到无人机的航迹通常是通过坐标点控制,可能会使实际的无人机飞行路线不一定是贝塞尔优化后的航迹。为此,本文提出了双层优化策略,其主要思想是对规划的航迹进行两次优化,以期达到更理想的效果。
设图3中P1、P2、P3是航迹中连续的3个点,航迹连接顺序为P1→P2→P3,β为航迹中相邻节点的转折角,根据角度的大小,对航迹进行优化。

图3 航迹优化图解
处理方法为:
第一次优化:当β>90°时,认为航迹比较平滑,不需要进行优化处理,航迹节点还是原来的节点;当β≤90°时,认为转折角度较大,需要进行优化处理。具体优化步骤如下:
(1)首先检查航迹P1→P3上是否有障碍,如果没有障碍,则删掉节点P2,直接连接P1和P3两点作为新的航迹;如果P1→P3上是有障碍,则取P2、P3的中点P;
(2)检查航迹P1→P上是否有障碍,如果没有障碍,则略过节点P2,连接P1、P两点作为新的航迹;若存在障碍,则不能改变原来的航迹,只能以P2作为节点,不进行优化处理;
(3)从航迹的起点开始依次检查每个节点与后两个节点的曲折情况,确定是否可以进行优化,并做出相应的处理,直到航迹终点,第一次优化完成。
以第一次优化完的航迹为基础,进行第二次优化,优化方法为:判断两条航迹之间的转折角β,当β>150°时,不进行优化;当β≤150°时,认为航迹较曲折,需要进行优化,具体优化步骤是只进行第一次优化步骤(2)、步骤(3),直到新航迹的终点,优化完成。
第一次优化过程的主要作用是对航迹中的节点进行删减,使节点数目更少,加快程序执行过程,并且对转折角小于90°的航迹进行优化,使航迹平滑,但是第一次优化由于改变节点,有可能使个别地方航迹的平滑度降低,所以进行第二次优化;第二次优化没有进行节点的删减,只对第一步优化的航迹中,转折角大于150°的航迹进行优化,增加航迹的平滑度。
3 突发威胁航迹规划、性能约束及任务空间模型
3.1 突发威胁航迹规划
根据任务需要,一般四旋翼无人机动态航迹规划可分为两种情况:一是执行运输、投送、打击任务时,四旋翼无人机只要能到达目标点即可,这种情况下可以放弃原先的航迹,以四旋翼无人机当前位置为起点,以目标点为终点重新规划一条航迹;二是执行侦察任务时,四旋翼无人机避过障碍后还要回到原来的航线上继续执行任务,这时只需要规划出一段可以绕过障碍物的航迹。
第一种航迹规划方式只要把当前位置设为起始点,终点为目标点即可,设置简单,但是当四旋翼无人机距目标点较远时,重规划航迹花费的时间较长,实时性降低,但是对于目标点改变的情况只能使用这种方式;第二种规划方法需要找出分离点和接入点,并且分别设为起始点和目标点,规划一条航迹,当四旋翼无人机到达分离点时按照新规划的航迹飞行,到达接入点时回到原来的航线上,通常这种方式规划航迹短,实时性高,但是对障碍物在目标点附近时没有必要采用此方式。
3.2 动态性能约束
四旋翼无人机能够正常飞行,需要满足其动态性能要求,主要性能约束如下:
最大飞行距离Lmax:设四旋翼无人机的航迹是由航迹段{lii=1,2,3,…,n}坐标组成,则约束可表示为

(3)
最小直飞距离lmin:设四旋翼无人机的航迹是由航迹段{lii=1,2,3,…,n}坐标组成,则约束可表示为
lmin≤li
(4)
最大转弯角度αmax:由于四旋翼无人机可以悬停,所以可以忽略此约束[16]。
最大俯仰角φmax:设三维航迹方程为z=f(x,y),ai为第i段航迹的水平投影,则ai=(xi-xi-1,yi-yi-1),该约束条件表示为
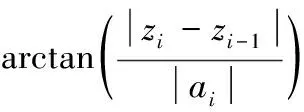
(5)
同时满足以上约束条件的航迹才是可行航迹。二维条件下不需要考虑四旋翼无人机最大俯仰角的限制,只需满足式(3)、式(4)即可。
3.3 任务空间模型
3.3.1 二维任务空间模型
二维模型是基于四旋翼无人机定高飞行时的情景,此时四旋翼无人机的任务空间R=[(X,Y)0≤X≤100,0≤Y≤100],(m)。其中X是任务空间的横坐标,Y是任务空间的纵坐标。在二维空间中,可以将障碍物建模为圆。二维任务空间和障碍物的建模如图4所示,Pstart、Pgoal分别是起始点和目标点,圆形区域是障碍物。

图4 二维任务空间模型
3.3.2 三维任务空间模型
实际中,四旋翼无人机是在三维环境中飞行,仿真需要给出三维环境下四旋翼无人机的任务空间描述,设其为R=[(X,Y,Z)0≤X≤100, 0≤Y≤100, 0≤Z≤100],(m)。其中X、Y、Z分别为任务空间的横坐标、纵坐标和竖坐标。障碍威胁可以用以下方程来描述

(6)
其中,Zi为第i个山峰的高度,(Xi,Yi)是第i个山峰的峰顶坐标,(Xλi,Yλi)为第i个山峰X方向和Y方向上的坡度。三维环境下的任务空间和障碍物模型如图5所示。

图5 三维任务空间模型
4 仿真验证与分析
为了验证与分析本文所提出的综合改进RRT算法的性能,在二维任务空间中进行仿真实验,并与两种具有代表性的RRT改进算法进行性能比较;同时分析综合改进RRT算法中的重要参数——引导概率θ对算法的影响。在三维空间中对两种类型的动态航迹规划进行仿真,验证综合改进RRT算法的可行性。
4.1 不同优化方法之间的比较
对传统RRT算法的改进,最典型的优化方法是加入引力使随机树尽可能朝着目标点方向生长来加快收敛速度和动态步长策略来改善算法实时性与航迹平滑度的矛盾。本部分将综合改进RRT算法与启发式RRT算法和动态步长RRT算法进行比较,分析各种改进型算法的特点。进行30次仿真比较,结果如图6、图7所示,具体性能指标由表1给出。

图6 综合改进RRT与启发式RRT的比较

图7 综合改进RRT与动态步长RRT的比较

比较类别综合改进RRT启发式RRT动态步长RRT随机树叶节点数/个Max544374Min353235Mean42.6437.1858规划时间/msMax105.39.7210.69Min8.094.765.38Mean21.76.887.64航迹长度/mMax134.2144.08135.97Min127.85130.84129.70Mean130.58136.01132.74
图6中细实线是启发式RRT算法规划的航迹,粗实线是改进RRT算法规划的航迹,“*”是启发式RRT算法的叶节点,“+”是综合改进RRT算法的叶节点。图7中细实线是动态步长RRT算法规划的航迹,粗实线是改进RRT算法规划的航迹,“*”是动态步长RRT算法的叶节点,“+”是综合改进RRT算法的叶节点。从图6、图7可以看出,启发式RRT算法在没有障碍物时规划出来的航迹几乎为直线,没有转弯角度,航迹最优,但是有障碍物时规划航迹转折角度较大,动态步长RRT算法完全由引力函数提供随机树生长方向和步长,航迹对引力函数依赖性很大,不利于适应复杂环境,综合改进RRT算法不仅对随机树的生长提供指引,而且对规划的航迹进行优化,航迹的平滑度优于启发式RRT算法和动态步长RRT算法。
从表1中可以看出,随机树节点数量上,启发式RRT平均需要37.18个节点就可以规划处从起始点到目标点的航迹,数量最少,效率最高,动态步长RRT算法仅依赖引力函数,平均需要58个节点才能规划出航迹,效率最低,综合改进RRT算法介于两者之间;从规划时间上看,启发式RRT算法和动态步长RRT算法相差不多,而综合改进RRT算法需要的时间大约是另外两种算法的3倍,这是因为启发式RRT算法和动态步长RRT算法规划完航迹后没有进行航迹的平滑度优化,而综合改进RRT算法的平滑度优化策略耗费了大量的时间;航迹长度上,综合改进RRT算法最短,这得益于对航迹的优化,启发式RRT算法最长,动态步长介于两者之间。
总体来说,启发式RRT和动态步长RRT算法实时性好,适合应用于障碍物较少,实时性要求高的场合;综合改进RRT算法的航迹最短,平滑度最好,但是规划时间最长,实时性最差,综合改进RRT算法是牺牲算法的实时性来提高航迹的平滑度的,在实时性要求不是很高的情况下可以选择综合改进RRT算法进行航迹规划。
4.2 算法参数影响
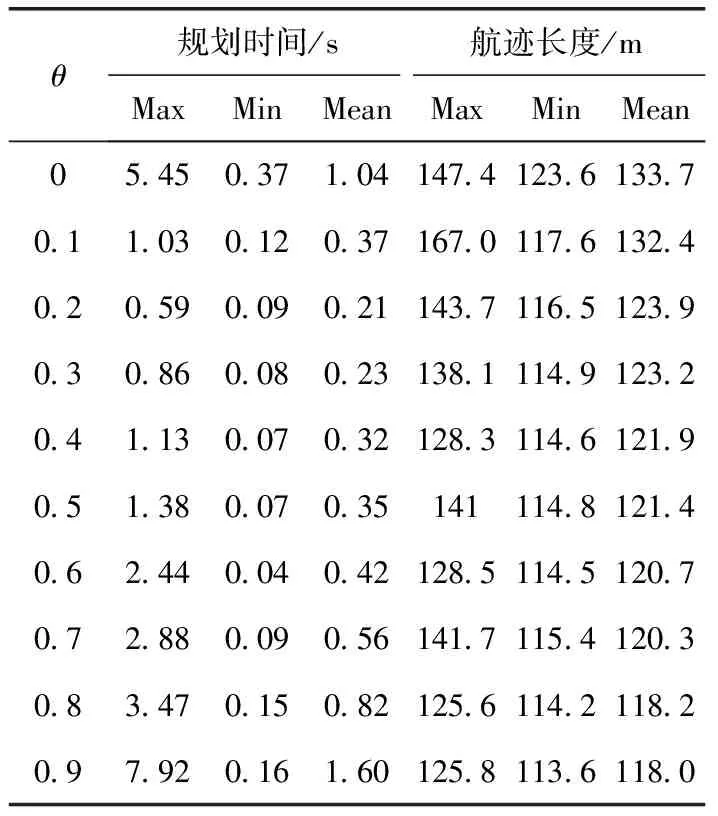
综合改进RRT算法中的参数有原始步长ε和引导概率θ。原始步长是根据任务环境、四旋翼无人机的动态性能约束和任务要求来确定的,引导概率θ则直接决定了算法性能的优劣。在图8所示随机任务空间中设置50个随机障碍,算法中步长设为5,在θ∈[0,1)的范围内,每隔0.1对θ进行取值,进行50次仿真验证,对规划距离、规划时间两项最重要的指标取平均进行统计,其结果见表2,θ取不同值时的性能比较如图9所示。

图8 随机任务空间
θ规划时间/s航迹长度/mMaxMinMeanMaxMinMean05.450.371.04147.4123.6133.70.11.030.120.37167.0117.6132.40.20.590.090.21143.7116.5123.90.30.860.080.23138.1114.9123.20.41.130.070.32128.3114.6121.90.51.380.070.35141114.8121.40.62.440.040.42128.5114.5120.70.72.880.090.56141.7115.4120.30.83.470.150.82125.6114.2118.20.97.920.161.60125.8113.6118.0

图9 θ取不同值时的仿真性能
由图9(a)可以看出,规划时间在θ=0.2时取得最小值,随着θ的减小或者增大,规划时间不断增加。这是因为θ取值很小时,算法的方向启发性不强,随机点在任务空间中生成的随机性很大,需要耗费较长时间随机树才会到达目标点;当θ取值很大甚至接近于1时,算法的方向启发性很强,搜索未知区域的能力明显减弱,随机树扩展的过程中遇到障碍时,需要重复搜索才能找到合适的叶节点,绕过障碍物,到达目标点,重复搜索的过程会耗费大量的时间,导致算法实时性降低。由图9(b)可以看出,航迹距离随着θ的增大而减小,特别是θ∈[0,0.2]时航迹减小比较明显。这是因为θ越大,算法的指向性越强,规划出的航迹越接近从起始点到目标点的直线。
当θ=0时,改进的算法相当于对传统RRT算法进行路径优化;当θ=1时,一直选目标点为随机点,失去算法的搜索性,容易导致航迹规划失败。仿真实验结果表明,θ取值不能过大也不能过小,过大会导致算法搜索能力降低,造成规划失败或者花费更多的时间搜索导致实时性降低;过小会导致算法启发性不强,路径曲折,达不到期望的效果。由仿真结果可知θ的取值在0.5左右可以取得较好的效果。
4.3 突发威胁航迹规划
当四旋翼无人机按照规划的航迹飞行,航迹上突然出现障碍物时,四旋翼无人机要具有重新规划航迹的能力。本部分对三维空间中综合改进RRT算法的两种类型的动态航迹规划进行仿真,设原始步长为ε=5、引导概率θ=0.5、障碍物半径为10,验证所提出的综合改进RRT算法的可行性。仿真结果如图10、图11所示。
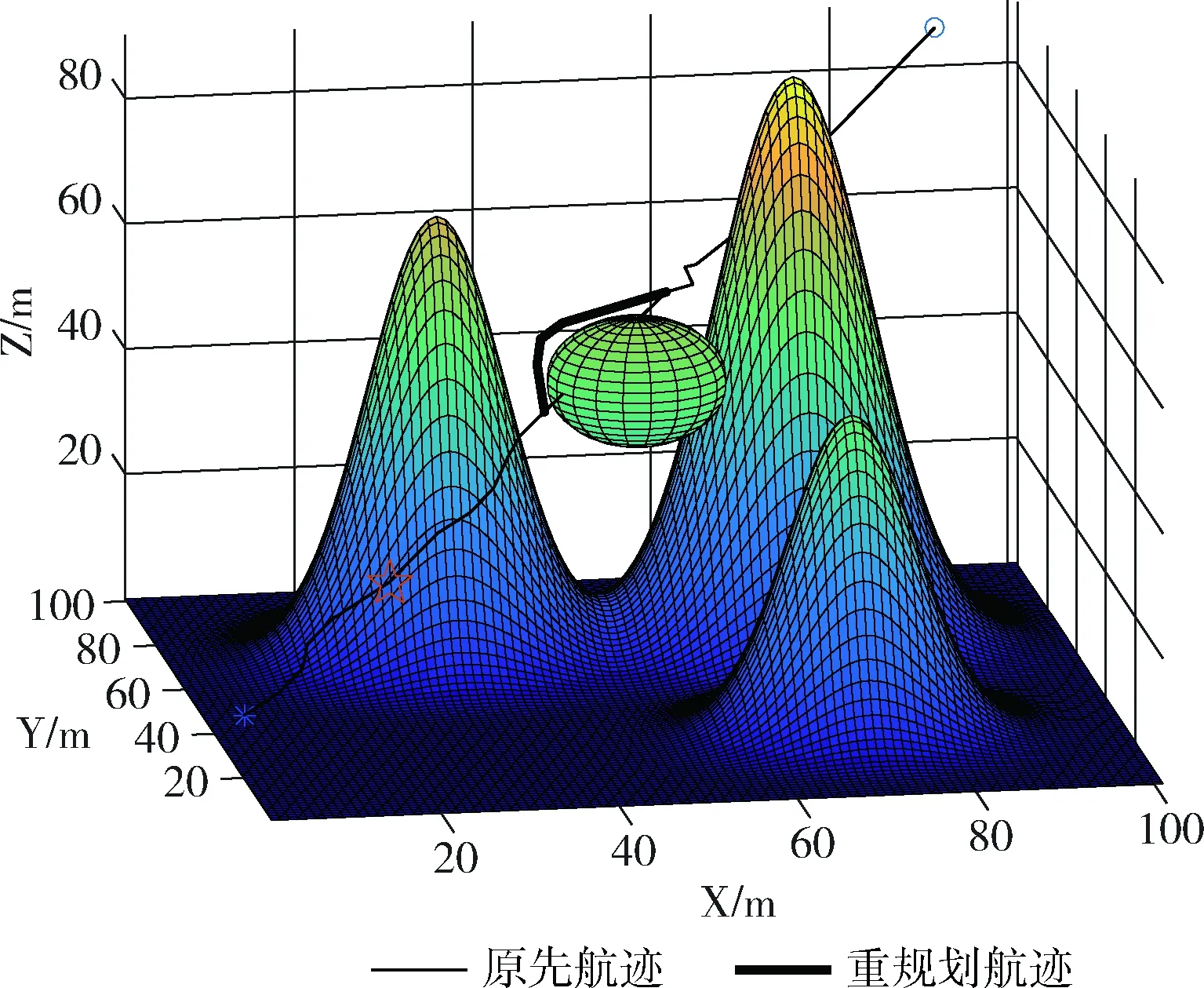
图11 绕过障碍,回到原来航迹
图10、图11中“*”是起始点,“o”是目标点,黑色细线是四旋翼无人机原先的航迹,黑色粗线是障碍物出现后重新规划的航迹,五角星是障碍物出现时四旋翼无人机的位置。两种动态航迹规划方式都可以重新规划一条绕过障碍物的新航迹,达到避障的目的,验证了综合改进RRT算法的可行性,实际应用中具体采用哪种方式要结合具体情况而确定。
5 结束语
针对传统RRT算法随机性强、收敛速度慢、规划航迹不平滑的缺点,本文受其它文献启发对其进行了改进,提出了综合改进型的RRT算法,并且与两种典型的RRT改进算法进行了比较,可以发现综合改进后的RRT算法航迹平滑度增加,但是规划时间增长,实时性降低。本文进一步在二维任务空间中对综合改进RRT的参数θ取不同值时进行仿真,验证了引导概率θ对算法的影响,并给出选取原则;在三维环境下将改进后的RRT算法用于两种动态航迹规划中进行仿真验证,取得了满意的效果,验证了综合改进RRT算法能够适应动态航迹规划的要求。
然而,基于RRT算法随机性强的特点,本文没有对最优航迹的选取进行研究,RRT算法与最优航迹选取算法的结合将是解决此问题的思路,也是以后研究的方向。
