基于Caffe加速卷积神经网络前向推理
2018-12-22吴俊敏
吴 焕,吴俊敏
(中国科学技术大学 计算机科学与技术学院,安徽 合肥 230000)
0 引 言
过去几年,ILSVRC(ImageNet large scale visual re-cognition competition)[1]中陆续涌现出一批经典的网络结构[2-7]。这些模型往往都具备预测精度高、计算量大以及内存占用率高等特点。为解决卷积神经网络的硬件需求和计算资源不匹配的问题,本文基于深度学习框架Caffe[8],对卷积操作提出了一种新的加速策略。目前,一种主流的加速方法是使用GPU通用计算。GPU凭借其高效的并行计算能力,能够快速处理大量数据。这在很大程度上缓解了神经网络计算量过大的问题,也促使了单机多卡、多机多卡的技术革新。然而,并不是所有硬件都支持GPU通用计算,比如arm等嵌入式设备以及Macbook等个人电脑。因此,如何在不支持GPU通用计算的硬件设备上加速卷积神经网络的前向推理是目前急需解决的问题。有研究结果表明[9],卷积层是卷积神经网络中耗时比例最高的部分,优化卷积操作可以在很大程度上提升神经网络的整体性能。Caffe卷积包含两个主要操作,一是im2col,二是gemm。本文通过增强这两个操作的访存连续性,从而加速卷积神经网络的前向推理速度。
1 相关工作
随着深度学习技术不断发展,加速卷积神经网络的需求与日俱增。过去几年陆续出现各种加速策略,总的来说有如下几种。根据卷积定律,时域中的卷积操作等效于频域中逐点相乘的复数乘法。该定律不仅适用于一维信号,对二维图像同样有效。为此,研究人员[10,11]提出用快速傅立叶变换(FFT)实现二维图像的卷积操作。理论上,卷积核尺寸越大,加速比就越加明显。然而,目前主流的卷积神经网络均采用小尺寸卷积核,因此无法保证该方法总是优于传统的实现方式。此外,在转换到频域之前,FFT卷积还要求对输入图像以及卷积核同时补零,进一步增大了内存开销。
卷积神经网络存在大量冗余[12]。不仅在层与层之间存在冗余连接[13],模型参数的比特位也存在冗余[14]。出于训练目的,传统实现通常采用单精度浮点数。而在推理阶段,可以将其替换成低精度定点数。有研究结果表明,在前向推理阶段将浮点数量化成定点数不会影响模型的预测准确率。结合单指令多数据指令集(X86上SSE4或者ARM上Neon),还可以同时处理多个8位定点。研究人员在此基础上进一步提出了二元权重模型[15-17]。在专用硬件的支持下,卷积中的乘加运算全都可以用加法实现。
在大型网络模型中,卷积层通常有上百个卷积核。虽然权值共享的特性已经在很大程度上减少了模型参数,但是网络尺寸依然很大。有实验结果表明[18,19],在不影响模型准确率的前提下,全秩卷积核可以分解成一系列基本的卷积核。模型参数不仅更少,卷积速度也更快。在此基础上,还有针对非线性单元和深层网络模型的相关工作[20]。
上述工作从各个角度提出了不同的加速策略。比如,快速傅立叶变换卷积、定点模型参数以及卷积核的低秩分解。与之不同的是,本文从访存连续性来加速卷积操作。
2 Caffe卷积
卷积操作本质上是求输入和卷积核的点积。简单来说,就是将卷积核从左到右,从上到下以一定的步幅滑动。每滑动一次,卷积核与所在位置的图像块做点对点的乘加运算。由于就地实现卷积的速度很慢,Caffe卷积以矩阵乘法的形式实现。结合MKL、OpenBLAS等高效的基本线性代数库,运算速度能够大幅提升。Caffe卷积包括两个主要的操作,一是im2col,二是gemm。Im2col全称为image to columns,负责将图像块展开成列向量。Gemm(general matrix-matrix multiplication)负责矩阵之间的乘法运算。
为了更直观地介绍Caffe卷积的工作原理,图1展示了一个简单示例。Memory一行展示了输入图像和卷积核在内存中的存储情况,Convolution一行是卷积操作的宏观表示,CaffeConvolution一行则是卷积在Caffe中的具体实现。数据块尺寸通常表示成[n,c,h,w]的四维形式,n表示输入或卷积核的数量,c表示通道数,h表示高度,w表示宽度。图1所涉及的数据块尺寸如下:输入(input): [1, 2, 3, 3];卷积核(kernel): [2, 2, 2, 2];输出(result): [1, 2, 2, 2];补零(pad): [0, 0];步幅(stride): [1, 1]。在im2col的作用下,输入(input)展开成矩阵data_col。每个图像块对应一个列向量,其中第一列(i1,i2,i4,i5,i10,i11,i13,i14)是第一个图像块,第二列(i2,i3,i5,i6,i11,i12,i14,i15)是第二个图像块,并以此类推。接着,以kernel和data_col为实参,调用矩阵乘法函数gemm,得到卷积结果(result)。至此,一次卷积操作完成。
3 优化策略
3.1 优化访存
通过转置操作改变输入图像的数据排列,可以同时提高im2col和gemm的访存效率。如图2所示,在输入图像(input)中,每个通道既可以表示成二维形式,也可以表示成一维的行向量。若以二维形式表示,数据按照宽度、高度、通道的顺序存储,(i1,i2, …,i9)是第一个通道,(i10,i11, …,i18)是第二个通道。Im2col操作负责将所有图像块展开,其中(i1,i2,i4,i5,i10,i11,i13,i14)是第一个图像块。在转置之前,要将第一个图像块展开,每次只能连续拷贝两个元素,即(i1,i2), (i4,i5), (i10,i11), (i13,i14)。而转置之后,每次就可以连续拷贝4个元素,即(i1,i10,i2,i11),(i4,i13,i5,i14)。输入图像往往有几十甚至上百个通道,因此,对于转置后的输入(transposedinput)而言,每次就可以连续拷贝上百个数据,即(i1,i10, …,i2,i11, …),(i4,i13, …,i5,i14, …),而转置前的输入(input)每次依然只能连续拷贝两个元素。除此之外,转置输入图像还顺带提升了gemm的访存效率。由图1可知,im2col后是卷积核矩阵(kernel)和展开结果(data_col)的矩阵乘法,也就是每个卷积核分别与每个图像块做点对点的乘加运算。在图1的data_col中,读取一个图像块相当于读取一个列向量。而在图2的data_col中,读取一个图像块相当于读取一个行向量。在以行优先存储的体系结构中,行向量的读取效率更高,因此矩阵乘法的执行速度也更快。
3.2 具体算法
算法1是Caffe im2col的具体实现,下面结合图1进行解释。第1行对应data_col的行数,第2行和第3行负责处理data_col的一行。根据for循环提供的索引,可以计算data_col目前所在位置的偏移dst_offset,并反推出input的偏移src_offset。若dst_address落在补零区(某些卷积层要求在输入图像周围补零,本文将这块区域称为补零区),给目标地址dst_address赋0。否则,将源地址src_address的数据拷贝到目标地址dst_address。最终,输入(input)被展开成矩阵data_col,每个图像块对应data_col中的一个列向量。
算法1:Caffe im2col
输入:输入图像(input)以及卷积操作需要的各种超

图1 Caffe卷积的实现细节

图2 改进后的im2col
参,比如补零(pad)、步幅(stride)等
输出:输入图像的展开结果(data_col)
(1)for卷积核的长度do
(2)for卷积输出中单个通道的高度do
(3)for卷积输出中单个通道的宽度do
(4) 根据索引计算dst_offset和src_offset
(5) src_address = base_address(input) + src_offset
(6) dst_address = base_address(data_col) + dst_offset
(7)if((不需要为输入图像补零)or(需要补零and当前位置在非补零区))then
(8) data_col[dst_address]=input[src_address]
(9)else
(10) data_col [dst_address]=0
算法2是算法1的改进版本,下面结合图2进行解释。与算法1相比,算法2的输入多了一块事先开辟的空间transposedinput,这块空间用来存储转置后的输入。因此,空间开销由原先的n*c*h*w变为2*n*c*h*w。值得注意的是,这块空间一旦分配完毕就可以一直使用,因此其开销不计入测量时间内。根据3.1小节,首先转置input并存入transposedinput。接着将data_col中的所有元素置0,这么做可以去除循环中的条件分支语句。最外面两层循环对应data_col的行数,最内层循环负责处理data_col的一行。根据for循环提供的索引,可以计算data_col的偏移dst_offset,并反推transposed_input中的偏移src_offset。之后,便如图2所示,批量拷贝源地址src_address处的数据到dst_address中。每次批量拷贝的数据量为kernel.cols*kernel.channels,即(i1,i10, …,i2,i11, …),(i4,i13, …,i5,i14, …)。算法2不仅能去除for循环中的条件分支语句,更重要的是通过转置提升了im2col和gemm的访存效率。
算法2: Optimized im2col
输入: 输入图像(input)以及卷积操作需要的各种超参,比如补零(pad)、步幅(stride)等。并事先开辟一块空间(transposed input),用以存储转置后的输入
输出:输入图像的展开结果(data_col)
(1) transposed_input = transpose (input)
(2) memset (data_col, 0)
(3)for卷积输出中单个通道的高度do
(4)for卷积输出中单个通道的宽度do
(5)for卷积核的高度do
(6) 根据索引计算dst_offset和src_offset
(7) src_address = base_address (transposed_input) + src_offset
(8) dst_address = base_address (data_col) + dst_offset
(9) memcpy (dst_address, src_address, kernel.cols * kernel.channels)
4 实 验
4.1 概 览
本节总共设置了3个实验,测试环境是Intel Core i5,OS X EI Capitan 10.11.4,BLAS库是Intel的MKL。默认情况下,Caffe采用gcc的-o2编译开关。为了更充分地利用编译器,改进前后的对比实验均采用-o3选项。第一个实验测试im2col、gemm以及总的卷积耗时。相比于im2col,gemm的计算时间更长,优化效果也更大。第二个实验测试通道数和输入图像尺寸对性能的影响。实验结果表明,卷积加速比最高可超过100%,平均加速比在40%左右。最后一个实验测试卷积核尺寸对性能的影响。
4.2 卷积耗时
本实验总共测试7种不同的通道数,测试内容包括im2col,gemm以及卷积各自的计算时长。出于制表目的,所有结果均四舍五入到最近的整数。如表1所示,相比于im2col,gemm的计算时间更长,优化效果也更加明显。容易看出,矩阵乘是Caffe卷积中非常耗时的一个操作,可以从两个方向进行优化。一是具体实现,二是访存效率。优化矩阵乘法的实现可以考虑使用x86上的SSE4或者ARM上的NEON。这些指令又称为SIMD指令,即一条指令可以同时处理多个数据。由于Caffe直接调用BLAS库,因此这部分优化工作由BLAS库的提供商负责。再者就是提升矩阵乘的访存效率,也正是本文所做的工作。若图像块以列向量的方式存储(如图1所示),每读取一个图像块都需要跨行读取,访存效率很低。而若以行向量的方式存储(如图2所示),就能连续读取所有图像块,大大提升了矩阵乘法的执行效率。
4.3 输入尺寸和通道数的影响
卷积层之间的输入尺寸和通道数往往不尽相同,为测试优化方法在不同卷积层上的加速效果,本实验测试了4种输入尺寸以及7种通道数。实验所用的配置如下:输入(input): [10,c,h,w];卷积核(kernel): [64,c, 3, 3];补零(pad): [1,1];步幅:(stride): [1,1]。没有固定的字母代表实验变量,其中c为通道数,h为高度,w为宽度。如图3和表2所示,128×128的加速效果最为明显,平均加速比高达93.18%。对于其它3种尺寸,加速比均在40%上下浮动。
4.4 卷积核的影响
除了输入图像,卷积层中的卷积核也不大相同,最常用的是1×1和3×3两种卷积核。出于完整性考虑,本实验加入了其它几种不常用的尺寸,总共测试6种卷积核。

表1 im2col,gemm以及卷积耗时
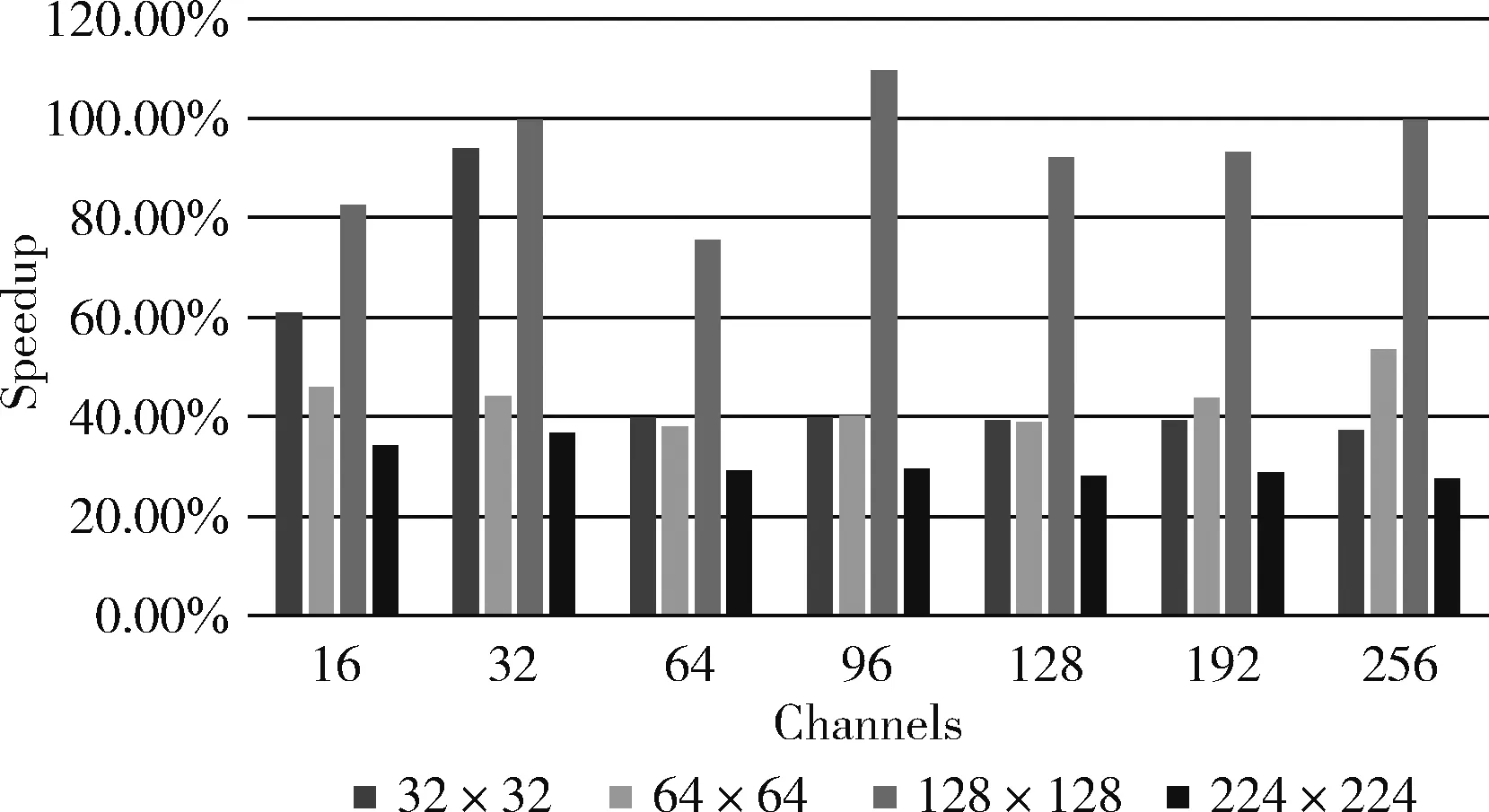
图3 不同输入尺寸和通道数的加速比
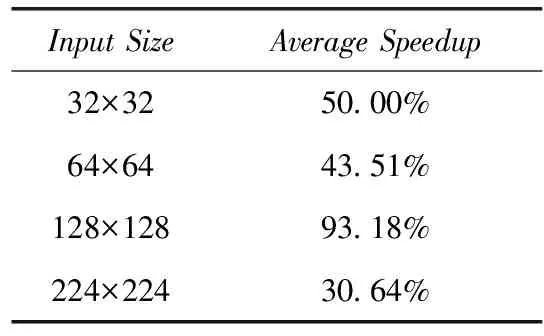
Input SizeAverage Speedup32×3250.00%64×6443.51%128×12893.18%224×22430.64%
需要注意两点,一是由于Caffe在处理1×1卷积核时没有用到im2col,因此本实验不测试这个尺寸。二是当输入图像的尺寸过小时,卷积时间很短,因此在4.3节没有测试本实验使用的几种输入尺寸,而是在本节直接给出运算时间,时间单位是微秒。如表3所示,虚线两边分别是改进前后的卷积时长。不论是哪种尺寸的卷积核,卷积速度均有不同程度的提升。
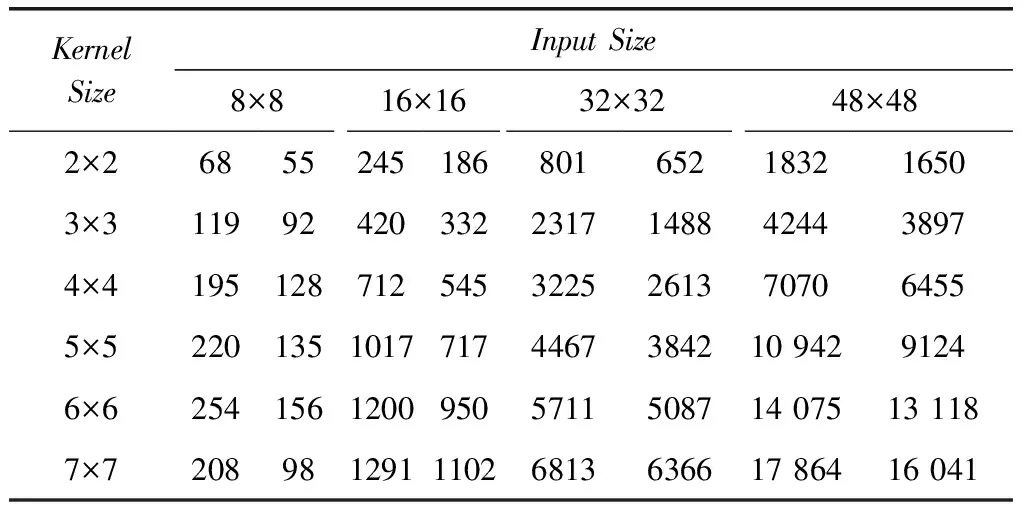
表3 不同卷积核的加速效果
5 结束语
为了加速卷积神经网络的前向推理速度,本文基于深度学习框架Caffe,对卷积操作做了两点优化。首先是优化im2col的拷贝速度。在展开输入图像的过程中,Caffe im2col每次都只将输入(input)的一个元素拷贝到data_col中。经过优化,每次就可以连续拷贝上百个元素。接着是矩阵乘法的访存连续性。在Caffe的原始实现中,每读取一个图像块都相当于读取一个列向量,访存效率很低。经过优化,可以以行向量的形式连续读取所有图像块,这在很大程度上提升了矩阵乘法的执行效率。实验结果表明,应用这两个优化点,卷积操作的平均加速比在40%左右。
