曼哈顿距离的思考
2018-12-22浙江省天台中学
■浙江省天台中学
曼哈顿距离的定义:曼哈顿距离也叫出租车几何,是在19世纪由赫尔曼·闵可夫斯基提出来的,它是一种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和。

图1
我们用通俗一点的语言来解释:如图1所示,直线①是A、B两点间的直线距离,我们通常把它叫作欧式距离,而其他几条线的长度就是这两点间的曼哈顿距离。虽然我们都知道两点之间线段最短,不过在生活中却不一定能直接来按照最短的那一条直线来走,因为我们只能走有路的地方,而不能“穿墙而过”。
曼哈顿距离与我们高中数学中的哪些问题相关呢?
问题:在平面直角坐标系中,定义d(P,Q)=x1-x2+y1-y1为两点P(x1,y1),Q(x2,y2)之间的“折线距离”,则圆(x-4)2+(y-3)2=4上一点与直线x+y=0上一点的“折线距离”的最小值是 。
分析:这里的折线距离就是曼哈顿距离,为了解决这类问题,我们先去研究 x +y的性质。对于 x +y=a(a>0),我们知道这个表示的是一个以原点为中心的平行四边形(准确地说是如图2所示的正方形),并且随着a值的不断变大,这个正方形也在逐渐变大,但对于每个正方形中的点(x,y),x +y的值保持不变。

图2
例1 已知2x+y=4,求 x +y 的最小值。
解析:如图3所示,当正方形与直线刚好相交时,x +y 的值最小,最小值为2。
例2 已知x2+y2=1,求x +y的最值。

图3
分析:如果将例1、例2题目中的结论“x +y ”改为“x-1+y-1”,则“以原点为中心的正方形”就改为“以(1,1)为中心的正方形”。那么我们可以得到以下两个结论。
结论一:已知直线l:Ax+By+C=0(AB≠0),P(x0,y0)是直线外一点,Q是直线上一点,过点P(x0,y0)分别作x轴,y轴的垂线,交直线l于点M,N,则:
(1)若PM=PN,则当点Q在线段MN上时,两点间的“折线距离”最小,最小值为PN或PM,并且此时直线l的斜率为±1,若点P到直线l的距离为d,则PN=PM=2d;
(2)若PM>PN,则当点Q在线段MN上时,两点间的“折线距离”最小,最小值为PN;
(3)若PM<PN,则当点Q在线段MN上时,两点间的“折线距离”最小,最小值为PM。

图4
结论二:若两条直线l1,l2平行,则l1上任意一点P(x0,y0)到l2上点Q的“折线距离”最小值都相等。根据上述结论我们可以建立如图4所示的平面直角坐标系,并定义d(P,Q)=x1-x2+y1-y1为两点P(x1,y1),Q(x2,y2)之间的“折线距离”,这样求本题的最值就转化为求圆(x-4)2+(y-3)2=4上一点与直线x+y=0上一点的“折线距离”的最小值。
解析:将直线x+y=0平移到与圆相切,求出此时的直线方程为x+y-7+22=0,利用结论二可知,圆(x-4)2+(y-3)2=4上一点与直线x+y=0上一点的“折线距离”的最小值是7-22。
高考衔接:已知a>0,函数f(x)=x2+x-a -3在区间 [- 1,1]上的最大值是2,求a的值
解析:令t=x2+x-a,x∈[- 1,1],本题等价于-1≤t≤5恒成立,并至少一边“=”成立。
t=x2+x-a,x∈[- 1,1]可以理解为点(x,x2)到点(a,0)的“折线距离”(其中点(x,x2)在y=x2上)。
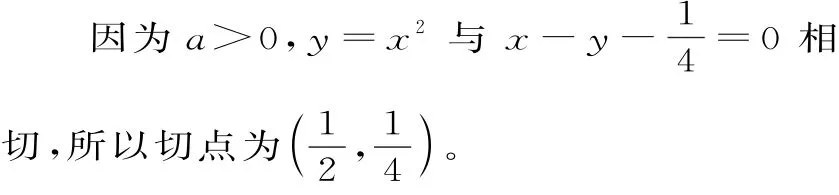
由图5所示的图像知点(-1,1)到点(a,0)的“折线距离”最大。


图5
