直接示教机器人的示教助力研究*

谢朝政，刘建群

(1.广东工业大学 机电工程学院，广东 广州 510006；2.广东省微纳加工技术与装备重点实验室，广东 广州 510006)

0 引言

直接示教机器人在某些工程(例如喷漆、抛光)方面具有相当大的作用，具备极高的友好性、高效性[1]，操作工在示教模式下直接用手操纵机器人执行器进行示教，无需掌握任何机器人知识和经验。机器人能通过示教点还原工作轨迹进行再现，方便快捷。

直接示教又分为功率级脱离示教和伺服级接通示教[2]。功率级脱离示教即是将机器人由人搬动，使机器人沿着预定的轨迹运动的一种示教方法；伺服级接通示教即是使用机器人执行器去间接搬动机器人手臂的一种示教方法，且机器人手臂和各驱动器之间不必脱离。在一般情况下功率级脱离示教需要相当大的劳动强度，并且操作不便，故大多数工业机器人采用伺服级接通示教的方法，同时在机器人执行器上加装多维力传感器，以便操作工用来引导机器人运动。Choi和Park[3-4]等对六关节串联机器人的直接示教系统进行了研究和开发，且在各关节装有力矩传感器。黄冠成[5]通过末端力传感器采集的受力信息在位置控制模式下对姿态进行角速度补偿，从而使直接示教操作更加柔顺。

一般的工业机器人质量和惯性较大，操作工直接示教的时候无法顺畅地进行操作，并且力传感器成本较高，示教效果会受到力矩传感器精度的限制，故采取一种免力矩传感器的控制方法，通过机器人各关节编码器获取的机器人运动状态求得机器人各关节力矩，从而可以通过助力的方式来减小操作工在示教操作中的阻力。为了获得在机器人末端助力所需的机器人各关节力矩，需要知道机器人各关节位姿及运动状态与关节力矩之间的关系。本文通过研究机器人动力学并建立相应的动力学模型来得到这些关系，从而能准确地对各关节进行助力。

1 动力学算法的选择

机器人动力学所要研究的是物体的运动状态和受力之间的关系。研究机器人动力学主要解决两个问题：正动力学问题与逆动力学问题。概括地说，所谓正动力学，是指已知作用于系统上的力，求系统的运动；而逆动力学问题则反之，是已知系统的运动，求此时作用于系统上的力[6]。在示教助力研究中，由于只须求出机器人在某种运动状态下各关节电机输出的转矩，故在此只讨论动力学逆问题。

研究机器人动力学可以采用很多方法，包括拉格朗日方法、牛顿-欧拉方法、高斯方法、凯恩方法等等，最主要的是牛顿-欧拉方法和拉格朗日方法。相对于拉格朗日方法，牛顿-欧拉方法建立方程容易，且由于其模型具有递推形式，计算量相对要少得多[7]，故本文主要采用牛顿-欧拉方法。

2 机器人助力方案的确定

机器人助力方案框图如图1所示。

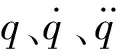
设机器人末端在示教时应受到的力为FT，示教人员所施加的力为FH。若不进行助力，要使机器人末端执行器沿着示教人员所需的轨迹运动，则可得:

FT=FH.

(1)

由式(1)可以看出，机器人运动所受的力全部由人力去承担，而一般工业机器人的自重都比较大，这会使得操作工劳动强度十分大。故可以让机器人在示教过程中处于一个通电状态，通过动力学算法使机器人各关节电机产生力矩，以减轻操作工在直接示教时所需克服的机器人自身关节的重力和惯性力。由于力矩的计算和控制都存在误差，计算值不可能和真实值完全相同，因此，力矩无法完全补偿，需要留有适当余量，以提高系统的示教稳定性[8]。故设置一个比例参数μA，使得助力小于计算值，从而既达到一定的助力效果又不至于助力过大产生不必要的效果及危险，即：

FA=μAFH.

(2)

其中:FA为通过助力所产生的力；μA为比例常量，一般取0<μA<1。

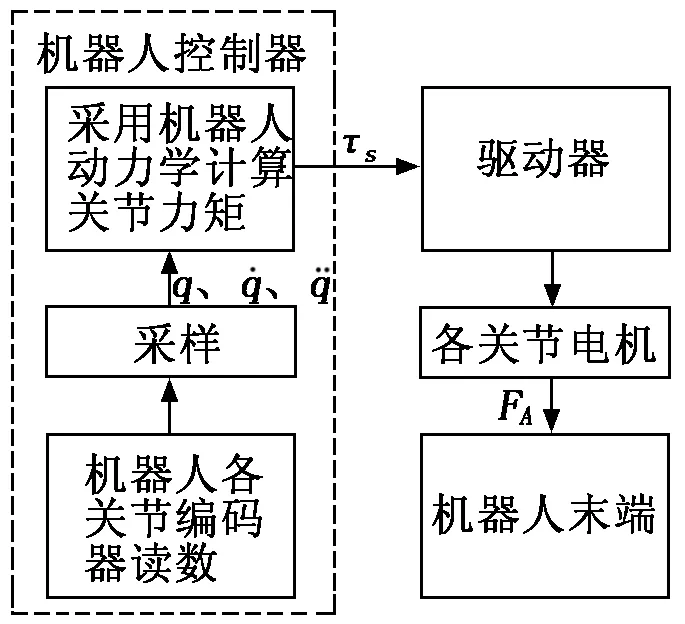
图1 机器人助力方案框图

3 建立动力学仿真系统

为了验证所建立动力学模型的正确性，建立一个动力学仿真系统。该动力学仿真系统流程如图2所示。以某六关节工业机器人为研究对象，首先用SolidWorks建立机器人三维模型。其次，一方面结合由三维模型得到的机器人各连杆质量、惯量等参数，采用牛顿-欧拉法建立机器人的动力学模型；另一方面，将建立的三维模型导入到ADAMS中进行动力学分析。最后，分别在动力学模型与ADAMS仿真模型中运行一段相同的轨迹并比较结果，从而验证动力学模型的正确性。

图2 动力学仿真系统流程

3.1 建立机器人三维模型

研究对象为某六关节机器人，采用SolidWorks建立机器人的三维模型，该三维模型及初始位姿如图3所示。

图3 六关节机器人三维模型及初始位姿

3.2 建立机器人连杆坐标系

采用D-H坐标系法表示机器人并对机器人进行建模，建立的机器人连杆坐标系如图4所示。

图4 六关节机器人连杆坐标系

4 建立机器人动力学方程

4.1 广义坐标的确定

4.2 刚体动力学算法和方程

牛顿-欧拉递推算法是常用的计算机器人逆动力学方程的方法，通过关节的初始角度、速度和加速度计算关节力矩。由于所研究机器人全部关节为转动关节，故最终可以写成如下形式：

外推：i:0→n-1

(3)

(4)

(5)

(6)

(7)

(8)

内推：i:n→1

(9)

(10)

(11)

最终可以建立出动力学方程，将关节力矩τ表示为各关节变量θ的函数。

5 机器人的动力学计算与仿真

5.1 动力学方程中各参数的计算

机器人各连杆的惯量矩阵可由SolidWorks软件通过三维模型计算近似得到，由于采用的是简化模型，故可以将各连杆简化为对于主惯量轴近似对称，故只研究其主惯量矩，则有：

5.2 动力学方程的计算结果

由于后三关节质量相对于前三关节很小，故只考虑前三关节质量，将3、4、5、6关节当成一个整体，其惯量矩阵发生了变化，连杆3的质量变为后四连杆质量之和。

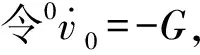
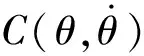
采用初始速度及终止速度均为零、最大速度为300°/s的五段三次S型速度曲线[9]进行速度规划，机器人各关节从初始位置(各关节角度为0°)正向运动1 s到达30°位置，生成一段运动轨迹。在动力学模型中运行这段轨迹，可以计算出各关节力矩，计算结果如图5所示。

5.3 ADAMS的仿真结果与动力学模型计算结果对比

将三维模型导入到ADAMS中进行动力学分析，使其与动力学模型运动一段相同的轨迹，绘制力矩曲线。ADAMS仿真结果与动力学模型计算结果对比如图6所示，ADAMS仿真结果与动力学模型计算结果的误差如图7所示。

通过图7可以看出，推导的动力学模型计算结果与ADAMS的仿真结果基本一致，最大误差不超过11%。

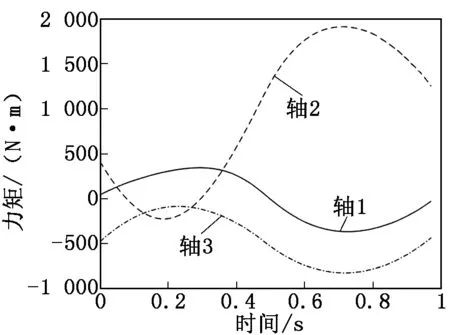
图5 动力学模型计算结果

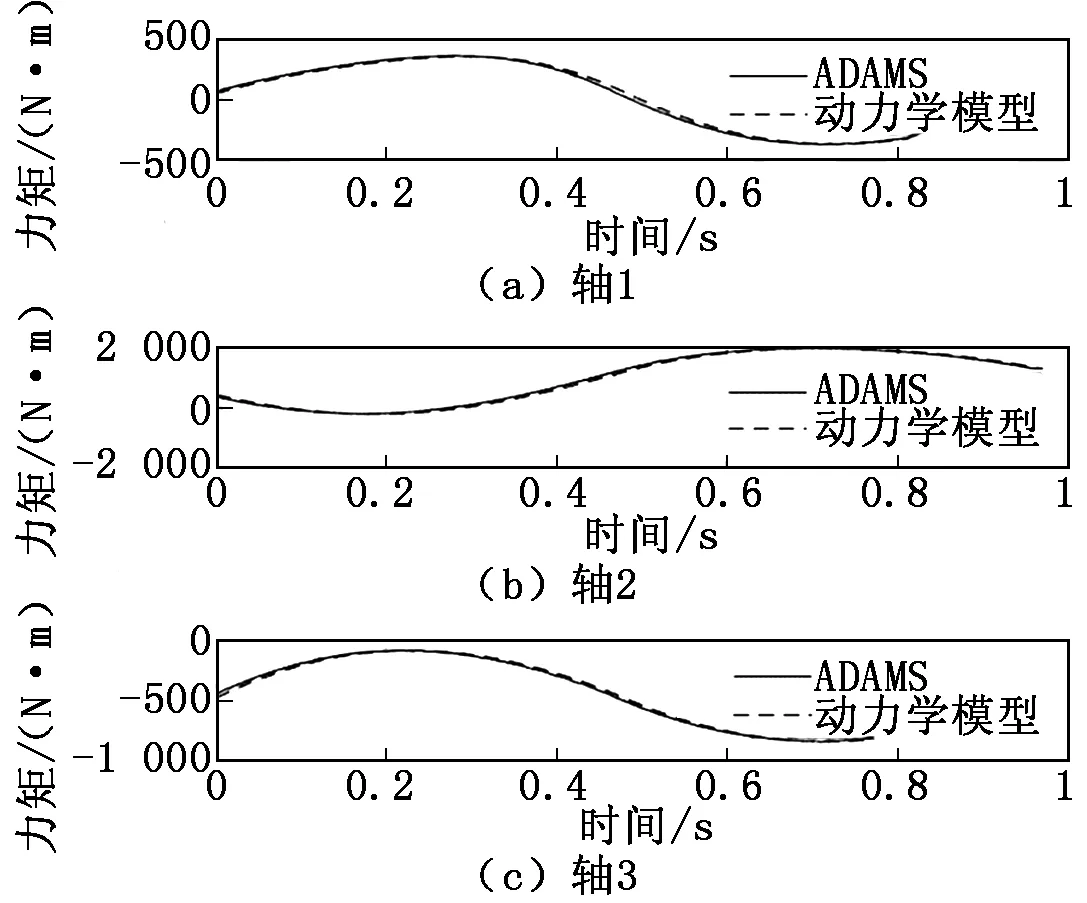
图6 ADAMS仿真结果与动力学模型计算结果对比

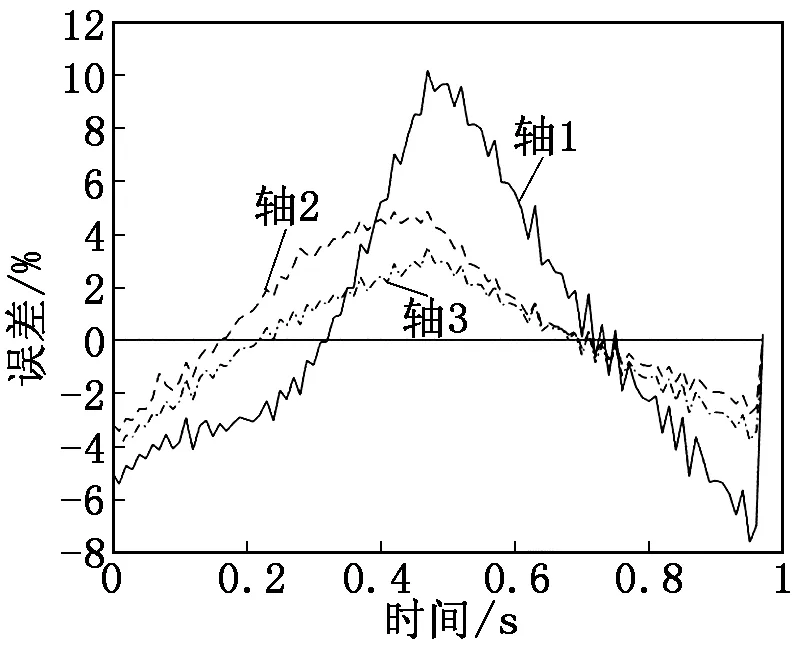
图7 ADAMS仿真结果与动力学模型计算结果的误差

5.4 示教助力

在示教过程中，传感器获取机器人运动状态信息，就能通过动力学模型得到机器人此时各关节的驱动力矩，这组关节力矩能够使机器人在不受牵引力的作用下自行向示教方向移动。但由于不可避免地存在误差，故设置一个比例参数μA使τA=μA·τ(0<μA<1)。其中，τ=[τ1τ2τ3]T为动力学所算出的各关节力矩，τA为助力系统最终助力力矩值。在力矩控制模式下，各关节输出力矩与其输出电压值成正比，即τ=k·ε(其中ε为各关节电机输入电压值，k为比例常数)。

设最终助力力矩值对应的电压输出为εA，则通过给各关节电机施加电压εA=μAε，从而达到一定的助力效果且保有余量，使系统更为安全。

6 结论

针对机器人直接示教助力方案进行了研究，基于机器人动力学建立了直接示教机器人的动力学模型，运用牛顿-欧拉算法，计算了动力学方程，得到了机器人在运动过程中各关节的力矩曲线，并与ADAMS仿真结果进行了对比，最大误差不超过11%。结果表明，建立的动力学模型正确，可为机器人的助力研究与力矩控制提供重要的理论依据。