凹凸率与平均值——琴生不等式的推广：凹凸率不等式

◎王礼斌

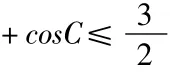
一、均值的概念

定义：对给定区间内任意 x1，x2（x1＜x2），当f（x）在该区间上连续且单调时，则称使等式 f（x0）＝p1f（x1）＋...＋pnf（xn）（p1＋p2＋...＋pn＝1，且p1，p2，...pn均为正数）成立的 x0称为 x1，x2，...xn的 n元 f（x）加权均数，p1，p2，...pn，分别为对应元素的权。

二、凹凸函数的几何特征

凹凸函数是区分函数增减方式的两种不同类型的函数，即：虽然函数单调增加，但却可以有如图的两种方式的增加，把形如f1（x）的增长方式的函数称为凸函数，而形如f2（x）的增长方式的函数称为凹函数。

根据函数的凹凸定义，不难证明，若函数 f（x）在区间 I是凹的，则函数－f（x）在区间I就是凸的。从而，我们从凸函数特征的讨论可在凹函数上适用。

为了便于使用，通常把不等式写成如下的等价形式：

如：设q1＝t，q2＝1－t，有q1－q2＝1.（q1，q2∈ （0，1））则（1）式可改写为

则函数式可写为

f（q2x2＋q2x2）≤ q1f（x1）＋q2x2

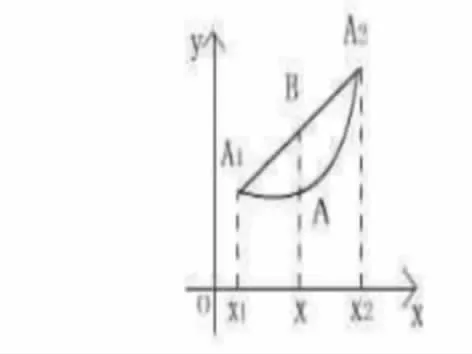
2、凸函数的几何特性：

如图，设A1，A2是凸函数y＝f（x）曲线上的两点，它们对应的横坐标 x1＜x2x∈ （x1，x2），则存在q1，q2＞0，q1＋q2＝1，使得x＝q1x1＋q2x2，过点x作ax轴的垂线交函数于A，交A1、A2于B，则上式左端即为A点纵坐标，右端即为B点纵坐标。因此，凸函数的几何意义就是：其函数曲线任意两点A1与A2之间的部分位于弦A1A2的下方或曲线在任一点切线上方。

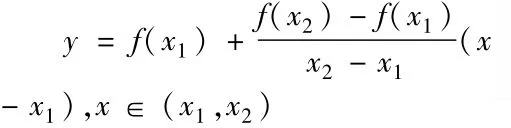
从而由上述凸函数几何性质有

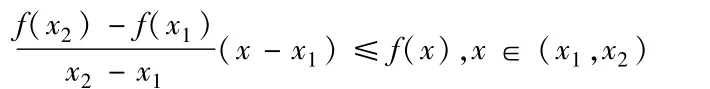
三、凹凸率与凹凸函数

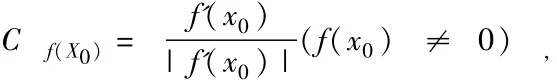
2、性质：设两连续且单调函数f（x），g（x）存在给定区间 D上的凹凸率函数。记为 Cf（x），Cg（x）分别为其凹凸率函数，若 Cf（x）＞Cg（x）在区间D上恒成立，则称g（x）在区间D上的凸性强于f（x）（或f（x）在区间D上凸性若于g（x））记分别为 x1，x2的 f（x），g（x）均数（x1，x2均定义区间且 x1≠x2g（x）），则有：

四、凹凸函数应用定理

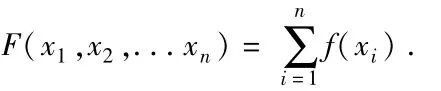
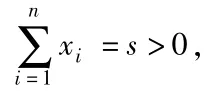
定理可以直接由控制不等式的理论得出，见定理5.5

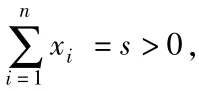
当然，若f（x）是严格凹函数，则定理1和推论1中不等号反向。

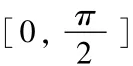
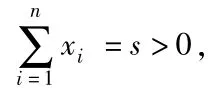
如同推论 1，设正实数 xi≤p，i＝1，2，...，n，其余条件不变，若 f（x）在区间［0，p］内是严格凸函数，则定理2中右边不等式是严格小于的，同样对于f（x）是凹函数时不等号反向。

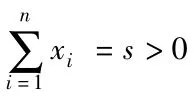
F（x1，s－x1，0...0）≤m.因此我们就有下面这个定理：

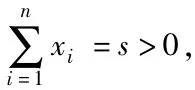
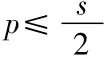
结语：综上所述，利用凸函数定义及几何特性证明不等式，关键的要根据所要证明不等式，选取相关的函数及适当的x1，x2选取，此法虽然具有一定的构造性，但证明的过程却相对简洁。