浅析在小学数学教学中进行的数学思想渗透教育
2018-12-20马振国
马振国
(甘肃省临夏回族自治州临夏县马集中心小学,甘肃 临夏)
一、小学阶段数学思想综述
(一)抽象思想
抽象思想主要指通过归纳多种事物之间的异同点,对异同点进行统一的归纳和整理,进而提取出多种不同事物之间的共性。通过不断地总结和归纳形成的一种固定的规律。在小学阶段教学中,基本的抽象思想是数学入门教学的重要内容。比如数字的形成就来源与抽象思想,教师在低年级数学教学中,会通过多种生活中常见事物的数量来强化学生对于数字的理解和认识。
(二)推理思想
推理思想指在已知的单个或多个判断中,通过合理的推理演绎出新的结论和判断的思维方法。推理思想是逻辑思维的重要组成部分和表现形式。因此在小学阶段教师适当地将推理思想引入到教学中可以很好地培养学生的核心素养,提升学生的逻辑思维能力。比如在小学课程中,教师在带领学生证明加法交换律、加法结合律和乘法分配律等基本运算规律时就可以使用简单的推理思想。
(三)建模思想
在数学学科中,建模思想一直以来都是一种形象描述问题、分析解决方法的重要手段。在针对问题进行建模过程中,多种图形、表格、公式等形象工具一方面有利于将抽象问题具体化,方便学生对问题进行理解;另一方面也可以通过建模式教学来帮助学生进行解决问题方法的教学。在小学数学课程中,通常在应用题的求解过程中广泛使用建模思想。
(四)数形结合思想
数形结合思想主要将数与形的有机结合来充分体现数与型之间的具体关系。这种方法在初中阶段广为运用,而在小学阶段较难的运用比较少,多在几何图形问题求解中。在小学阶段教师主要通过对几何体多种体积、面积的计算来培养学生初步教数形结合思想。
二、数学思想在当前数学课堂中的渗透
(一)收集整理数学思想
教师作为课程的主体,所以在课堂教学中教师需要根据知识点的具体特点通过多种数学思想工具的解释来对学生进行全方位的教学演示,让学生在理解知识点意义的同时学会多种数学思想。所以说数学思想教学的第一步骤是需要教师充分地整理数学思想与数学知识点间对应关系,通过积极对应的方式来帮助学生理解。具体来说,比如在小学四年级下册中加法运算定律、乘法运算定律的课程讲解中,教师可以在课前通过对加、乘法运算定律的核心概念运用多种方法和手段为学生讲解,并介绍相应的数学思想。
(二)合理呈现数学思想
由于数学思想具有一定的抽象性,所以在根据图像的抽象程度教师需要按照相关的形象工具来帮助学生进行理解。在相关呈现方法上,教师可以通过多种手法来开展,比如数学思想口诀、儿歌、规律图表、模型模组等形式来进行数学思想的渗透教学,从而保障学生的学习效果。当前在小学阶段,通过思维导图的模式来教授数学思想可以达到较好的效果,教师可以将相关知识点间的关系、数学思想通过思维导图呈现出来,以此帮助学生进行生动和形象的记忆。教师在课堂中将思维导图呈献给学生后,也可以在后期复习时让学生自己对知识点进行思维导图的描绘,从而形成数学知识点到数学方法、数学思想体系式的学习模式。
三、多重渗透数学思想
数学思想属于一种比较高级的知识,所以在具体教学活动开展过程中,教师需要对知识点进行多种数学思想交互渗透的教学手法予以开展,这样才能最大限度地保障数学思想的教学工作能够收获到实际的教学效果。比如在加法交换律的教学时,首先教师可以通过具象化的思想来为学生对加法交换律的主要内涵进行介绍,如题目“小明上午走了48km,下午走了36km,总共走了多少km?”在此题目的基础上,教师可以问同学们“如果上午走36km,下午走48km,则小明总共走了多少km?”这种推理论证的方式可以直接帮助学生对相关题目进行解释;同时教师还可以在设计实际问题引导学生推理的同时通过图形的方法来对学生进行交换律的解释,图表建模的方式可以帮助充分理解交换律的具体意义,形象且直观。
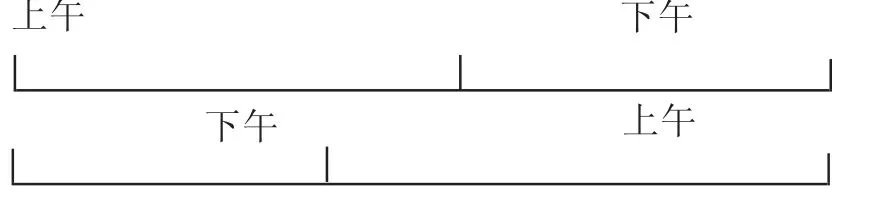
图表建模数学思想在交换律教学中的应用
从上面的图表我们可以看出,无论是上午加下午还是下午加上午,其总路程是不会变的,两种不同的运算方式,其结果是一样的的,线段的总长度是相同的,这就是加法交换律的特性。
在小学数学教学中,基于新课改对于数学教学的影响和作用,其教学要求的中心就是培养学生的数学核心素养,需要强化学生数学思想的构建与提升。广大小学教师需要认真进行教学研讨,探索小学生数学思想培养有效途径,深化小学数学教学效果。
