基于ANSYS Workbench的压力容器封头设计

计雪洁 张 陈

（1.沈阳工程学院，沈阳 110136 a.研究生部 b.机械学院）

压力容器是现代工业生产中，尤其是化工行业中不可或缺的重要设备之一，设计时必须保证其安全可靠。为确保压力容器安全有效运行，保障人民生命财产的安全，必须十分重视压力容器的设计。随着科技的发展，新材料的不断涌现，压力容器朝着大型化、高参数的方向发展，对压力容器设计提出了更高要求。目前，常用的压力容器设计的方法大致分为两种，即传统设计和计算机模拟仿真设计。传统设计中，由于压力容器实际工作中受载和环境复杂，无法按照理论公式或经验公式有效进行设计，为满足强度设计准则确保安全引入过高的安全系数，造成一定的浪费。近些年，随着计算机技术的飞速发展，有限元分析在压力容器设计领域得到了广泛应用，它可以有效模拟出压力容器在实际工作中的受力状态，清晰看出其危险截面和最大变形处，有针对地进行设计和改进。

本文主要针对一种内压薄壁圆筒压力容器，封头为椭球和平板，利用ANSYS有限元进行分析比较，结合理论计算，模拟分析两种封头的应力分布特点，并根据受力情况说明各自在工程中的应用。

1 压力容器参数描述

筒体内径400mm，壁厚6mm，长度3000mm，椭圆长短轴之比为2，壁厚6mm，圆平板直径412mm，壁厚6mm，容器及封头材料均为0Cr18Ni9，容器初始压力为0.2MPa，然后加压至0.4MPa和0.6MPa，分别模拟三种压力下容器封头的受力分布及变化。

2 理论计算

本设计中t、R关系如下式所示。

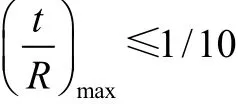
满足回转薄壳的无力矩理论，可列出微元平衡方程和区域平衡方程。

式中，σφ为轴向力，σθ为轴向力，R1、R2为第一曲率半径和第二曲率半径，rm为容器所取截面处的半径，α为所取截面的经线切向与回转轴的夹角。其中，转薄壳仅受气体内压作用时，各处压力相等，解出：

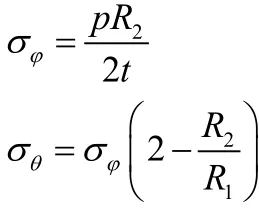
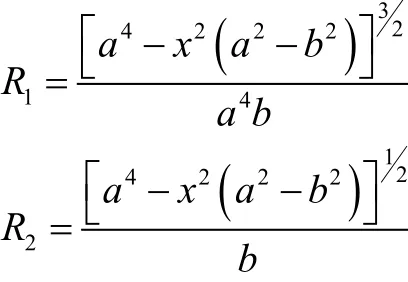
带入可得：

当a/b=2，为工程上常用的标准椭圆形封头，可以求出pa/tσθmax=σφmax=pa/t，位置出现在椭圆封头顶部。

平板封头属于周边固支，最大应力出现在板边缘上下表面处，其值为：

比较二者最大应力可知，平板是椭圆的25倍左右。

3 压力容器模型建立

用于ANSYS分析的模型可以有两种途径获得，一种是借助其他的CAD三维绘图软件，完成后以IGS的文件格式导入ANSYS；另一种就是利用ANSYS自带的workbench进行建模。由于本例中模型比较简单，所以直接利用workbench进行建模。只分析封头的应力分布，所以忽略了压力容器的一些其他辅助件。

4 网格划分，确定边界条件

模型建立后，对其进行网格划分如图1所示。由于模型中筒体的尺寸相对较大，而且重点分析椭圆形封头和平板封头的应力分布，整体网格划分后，对两种封头局部进行细化。载荷施加以0.6MPa内压为例，施加在压力容器内壁，如图2所示。

图1 模型及网格划分

图2 载荷施加（0.6MPa，内压）

5 应力分布及结果分析

应力分布云图如图3所示，平板应力最大点出现在与筒体接触的边缘处，当内压为0.6MPa时，最大值为423.33MPa。椭圆封头应力如图4所示，最大点出现在顶点处，最大值为23.64MPa。二者最大值出现的位置与理论公式一致。其他两种载荷下的情况与此相似，这里就不再赘述。

图3 平板封头应力分布云图

图4 椭圆形封头应力分布云图

三种不同载荷下的最大应力在表1中列出。表中分别列出理论值和模拟值，比较可知，平板封头的模拟值比实际稍小，椭圆封头比实际稍大，ANSYS模拟的三种情况，二者应力最大值的比值约为18.08，比理论值25稍小。

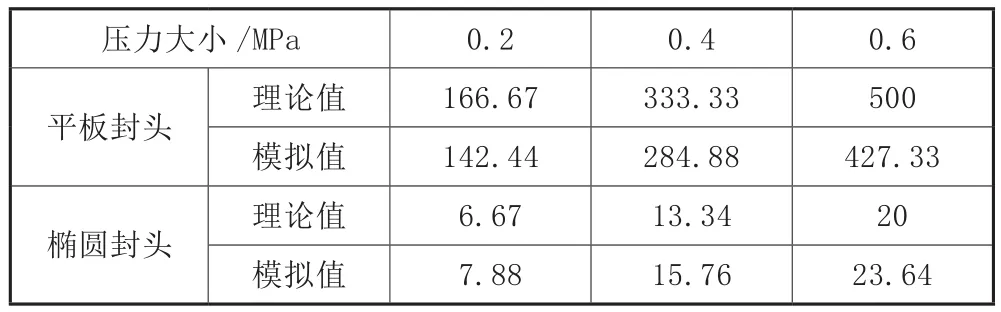
表1 不同应力下两种封头的最大应力

6 结论

通过理论计算和ANSYS模拟，可以得出以下结论：（1）压力容器平板封头的最大应力出现在边缘处，椭圆形封头最大应力出现在顶点处；（2）承受相同压力并且厚度相同的平板封头和椭圆封头，二者的最大应力相差约25倍左右。

由于ANSYS分析过程中模型建立的准确性、网格划分的精细程度、载荷施加的合理性等因素的影响，所以模拟值与理论值有一定差距，但足以说明平板封头的应力远大于椭圆形封头。

平板封头结构简单，制造方便，在压力不高，直径较小的容器中，采用平板封头比较经济简单。

椭圆形封头比表面积较小，标准封头与筒体等厚，承压能力较大，而且易于冲压成型，因此，在压力容器设计中应用最为广泛。

综上，在实际压力容器封头设计中，我们应充分考虑两种封头的特点，在满足安全性和经济性的前提下，合理运用两种封头。