滚转稳定平台抗高过载结构优化设计与分析

魏晓凯，李 杰,2，冯凯强，张 樨，李金强，鲁正隆

（1.中北大学 仪器科学与动态测试教育部重点实验室，太原 030051；2.中北大学 电子测试技术国防科技重点实验室，太原 030051）

精确测量弹体的姿态、位置、速度等导航信息参数是实现炮射导弹发展的一个重要环节[1-2]。惯性测量系统不受外界干扰，能够同时提供速度、姿态、位置信息，因此，研究惯性测量系统在炮射导弹上的有效应用具有重要的工程意义。对于炮射导弹而言，炮弹在飞行过程中，会受到巨大的过载作用，使得弹载惯性测量系统面临比较恶劣的测试环境，这就要求惯性测量系统在不破坏其威力的前提下具备抗高过载、成本低、体积小、可靠性高的特点[3]。

弹丸在炮膛内发射瞬间，所受到的发射过载可达上万g[4]，并且在后续飞行过程中还会受到增程发动机的过载，安装在弹丸内部载有惯性测量系统的滚转稳定平台在此阶段会承受巨大的冲击过载，此时平台的抗过载性能直接决定了在后续测试过程中平台能否有效运转。

为解决炮射导弹发展过程中高过载环境下的惯性测量问题，国内外学者进行了相关的研究工作，但目前对高过载环境下惯性测量的研究主要集中在电路设计、器件设计、测试标定及误差补偿等方面，对抗高过载惯性测量结构设计方法的研究和分析相对较少[5]。为此，针对发射高过载及连续过载的恶劣弹载环境，结合炮射导弹的测试需求，以保护滚转稳定平台为目的，本文提出了一种滚转稳定平台抗高过载结构设计优化方法。该高过载结构能进一步增强炮射导弹环境下滚转稳定平台的稳定性，增强其抗干扰与抗过载能力。分析与验证表明，该结构可以为惯性传感器提供稳定的测试环境，提高炮射导弹的测试精度。为滚转稳定平台在炮射导弹环境下的有效应用奠定试验基础。

1 滚转稳定平台工作原理

抗高过载滚转稳定平台是基于重力作用下的复摆运动原理而设计，图1为复摆运动简图。

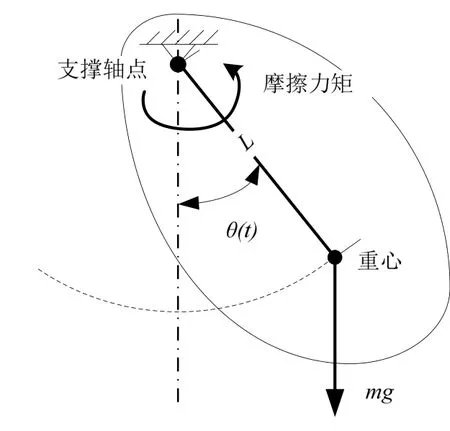
图1 复摆运动简图Fig.1 The motion diagram of compound pendulum motion

当外力矩为稳定的驱动力矩时，复摆会在重力矩与外力矩共同作用下，在一个平衡位置附近保持稳定的往复摆动[6]。

滚转稳定平台是用来搭载惯性传感器的一种机械装置，其组成如图2所示。在高旋弹体内部将微惯性测量组合（MIMU）安装在不与载体固连的滚转稳定平台中，平台建立一个复摆式的质量偏心结构，前后侧利用轴承连接平台外部结构，从而隔离了外部的高速滚转运动[7]。在运转过程中，平台在重力矩与轴承摩擦力矩共同作用下，绕滚转轴保持小幅度稳定摆动，此时平台与弹体滚转轴实现角速率隔离，在俯仰与偏航方向仍和弹体保持捷联。

在弹尾端设计有抗高过载结构（包括轴向承载装置和径向承载装置），确保在炮弹发射过程中轴承正常运转及平台正常工作。滚转稳定平台内部安装有微惯性测量组合（MIMU）和位置姿态解算模块，平台和弹体之间相对转速信息通过光电编码器测出并传送至平台内部的解算模块[8]。

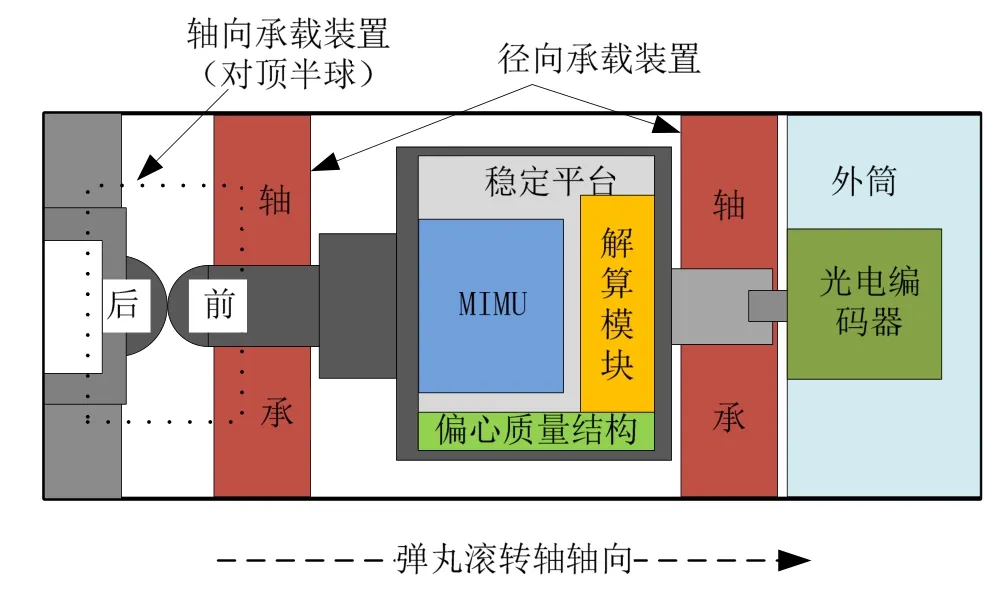
图2 滚转稳定平台组成原理图Fig.2 Schematic diagram of the semi-strapdown roll stability platform

2 抗高过载结构机理及设计

2.1 抗高过载结构机理

炮射导弹的运动状态一般分为四个阶段，即膛内发射阶段，中间惯性飞行阶段，增程发动机推送阶段和最后惯性飞行阶段。

所以，弹丸内部的滚转稳定平台所受轴向过载的来源主要包括：膛内发射过载、平台重量和增程发动机的推动过载。根据轴向所承受过载的特点，设计优化了抗高过载结构装置即“空腔”处理的对顶半球结构。

抗高过载结构组成如图3所示，分为后半球和前半球两大部分，后半球与弹体以螺纹的形式固联，前半球为稳定平台的一部分。

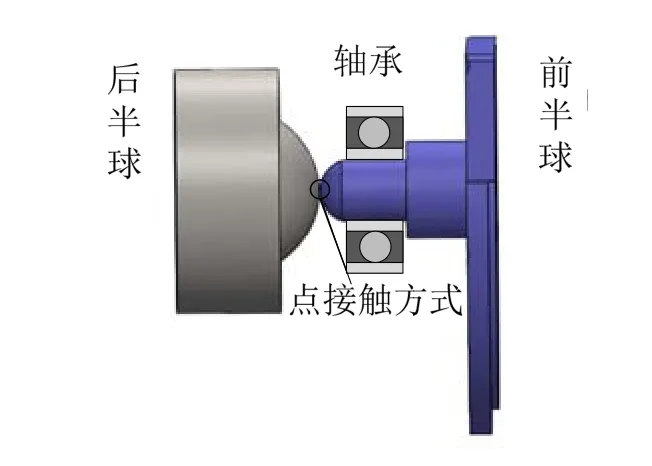
图3 抗高过载结构示意图Fig.3 Schematic diagram of anti-high overload structure

膛内发射阶段，弹丸内稳定平台在轴向受到巨大的冲击过载，此时抗高过载结构对顶半球接触，承受大部分轴向冲击过载，确保轴承和滚转稳定平台正常工作。图4为膛内发射阶段对顶半球状态。对顶半球结构此时产生弹性形变及较小塑性形变而暂时分离，并在后续受力时能再接触承受过载，防止后续在弹丸受发动机推力时抗高过载结构“机械失效”。

图4 膛内发射阶段对顶半球状态Fig.4 The state of counter-top hemisphere during the launching phase

弹丸惯性飞行阶段以惯性自由飞行为主，该阶段弹丸受到重力和空气阻力的共同作用，其中重力方向始终竖直向下，空气阻力的方向与弹药速度方向相反。此时对顶半球结构处于分离状态，如图5所示。

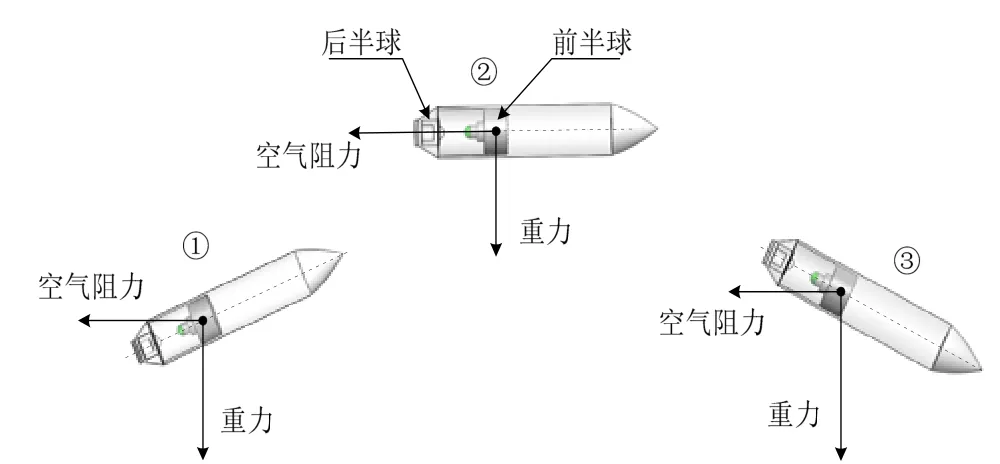
图5 惯性自由飞行对顶半球状态Fig.5 The state of counter-top hemisphere during the inertial flight phase

在弹丸惯性自由飞行阶段，为了使得对顶半球可以处于分离状态，所以在承受膛内过载时要存在一定的形变量。为了保证弹丸的有效射程，仅依靠膛内发射阶段赋予弹丸的初始动能是不够的，所以在弹丸飞行过程中存在增程发动机推送阶段。弹丸在发动机推送阶段的受力情况如图6所示。

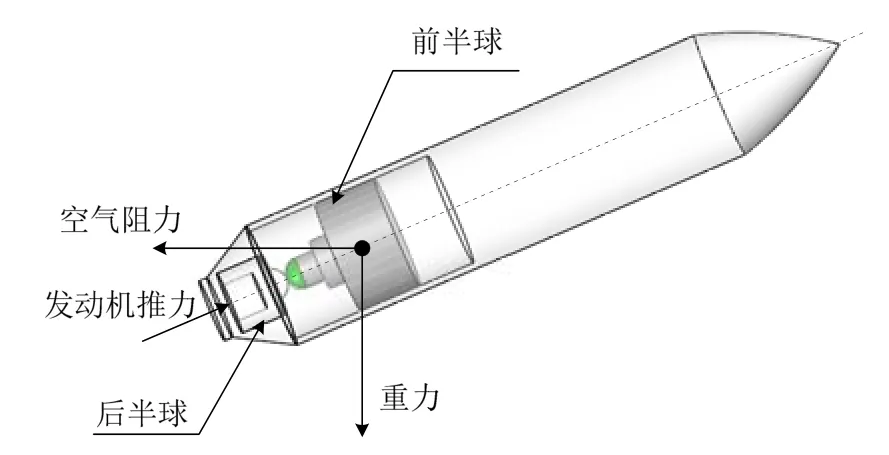
图6 发动机推送阶段弹丸受力简图Fig.6 Force of projectile during the engine push phase

在系统内部，轴承起着隔离弹体高速滚转角速率的作用。当滚转稳定平台的重力回复力矩确定以后，轴承摩擦力矩成为影响平台摆动角速率的决定性因素。将因对顶半球接触而引入的摩擦力矩定义为接触摩擦力矩。轴承摩擦力矩与接触摩擦力矩都因弹体的转动而产生，对滚转稳定平台起带动作用，所以两者的作用方向相同，不利于平台的稳定。为了确保滚转稳定平台的稳定性，在不改变发动机推力的基础上，通过减小力臂的方式来减小接触摩擦力矩。所以缩减对顶半球接触面积，可将对顶半球的前后半球尽量保存完整，将接触方式变为点点接触的形式。

2.2 抗高过载结构设计原则

由于炮射导弹特殊的应用环境，考虑滚转稳定平台的弹载稳定性及抗干扰性需求，要求抗高过载结构除了具有一般机械设计承受载荷、安装组件和提供构型的特征外[9]，还应满足以下要求：1）针对膛内发射段产生的高过载，通过对顶半球产生形变量缓冲过载对轴承产生的轴向压力；2）发动机推进加速段，对顶半球会再次接触，要保证两个半球以点点接触结构接触，减小摩擦力矩；3）前半球作为稳定平台的一部分与惯性测量组合捷联，要保证前半球形变尽量小；4）弹药惯性飞行阶段，对顶半球分离；5）对顶半球以点点接触缩小力臂方式减小对顶半球处产生的摩擦力矩，实现承载时的微小变形以减小平台的摆动幅度；6）对顶半球结构的形变不影响轴承的正常运转。

2.3 抗高过载结构优化设计及材料选择

基于上述工作原理及针对上述设计要求，设计了如图7所示的承高过载的对顶半球结构，图7为图3对顶半球部分的具体示意图。

图7 对顶半球结构示意图Fig.7 Schematic diagram of counter-top hemisphere

当平台轴向存在较大的过载时，轴承内圈会发生一定的轴向弹性形变，对顶半球接触并承受轴向的大部分过载，在此期间半球顶端会产生一定的形变，轴承也会产生一定的弹性形变，由于轴承的内圈本身存在一定的轴向活动余量，所以轴承产生的不可恢复形变相对较小。当滚转稳定平台的轴向载荷显著变小后，对顶半球之间则由于塑性变形产生一定的间隙分离。

为了保证 MIMU的敏感轴与弹体重合，要使得MIMU的固连面平整，且在弹丸惯性飞行阶段时对顶半球前后半球分离，所以对对顶半球后半球进行空腔处理，在保证对顶半球顶球完整性的前提下将因膛内过载产生的形变量转移到顶球的根部位置，如图8所示，达到保证弹丸惯性飞行阶段对顶半球前后半球处于分离状态，且使得弹丸在发动机推送阶段对顶半球的接触方式为点点接触。

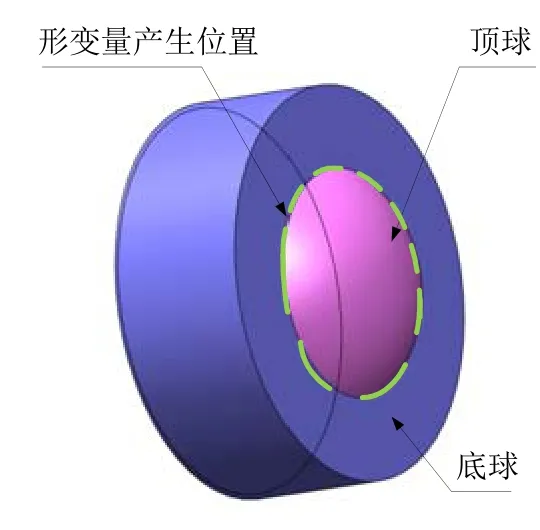
图8 对顶半球后半球Fig.8 Forward hemisphere of counter-top hemisphere

根据需求确定对顶半球结构材料并进行相应的工艺处理。30CrMnSi钢为高强度调制结构钢，具有很高的强度与韧性，多用于制造耐磨零配件或高负载的各种零配件。所以前后半球选用硬度相对较高的高强度合金结构钢30CrMnSi，并对对顶半球后半球采用亚温淬火加中温回火工艺处理。对 30CrMnSi钢采用亚温淬火加中温回火工艺处理，其淬火温度低，晶粒比较细小，晶界总面积增加，根据Hall-Petch关系可知，此时细晶强化作用明显，可以在保证硬度的基础上充分提高韧性，尽可能的保持对顶半球的完整性，保证过载后的点接触不变。

2.4 轴承选择

轴承的主要作用是承受稳定平台在径向所受的载荷，同时又要保证稳定平台与弹体之间在弹体滚转轴产生的摩擦力矩尽可能的小。因此要求所选轴承同时具有承载轴向载荷与径向载荷的能力，摩擦系数要求尽可能小，从而可以使得平台在所受到的接触摩擦力矩较小，有助于平台的稳定，并且要保持平台与弹体的滚转轴同轴。深沟球轴承可以同时承受径向载荷和轴向载荷，其结构简单，与其他类型的轴承相比容易达到较高的制造精度。综合以上因素，最终选择使用深沟球轴承，轴承在受到轴向过载时产生相应的弹性形变，保证轴承受到过载时能正常运转，同时通过弹性形变实现对顶半球大过载后的分离。深沟球轴承承载示意图如图9所示。

结合滚转稳定平台的内部尺寸、载荷等因素，为保证轴承运转精度，轴承游隙选择较高的精度等级，故轴承可以产生的轴向移动相对较小。最终选定的深沟球轴承主要参数如表1所示。

图9 深沟球轴承承载示意图Fig.9 Schematic of loading of deep groove ball bearing

表1 轴承参数Tab.1 Bearing parameters

3 抗高过载结构性能分析

3.1 抗高过载结构的有限元模型建立

为了模拟抗高过载结构在弹丸运动阶段下的状态，对其进行动力学仿真，主要对膛内发射阶段及发动机推送阶段进行仿真。

在ANSYS中设置选用材料对应的屈服强度与切变模量，表2为模型材料的基本属性。对该结构进行非线性显示动力学分析，首先将结构的承载部分简化，后半球边界约束条件为半球圆柱侧面设置为固定支撑面。

网格划分采用合理的划分精度等级完成自由网格划分。对结合面的处理采用ADD或ULLTE布尔操作命令进行连接，分析结果包含了由于忽略结合面而带来的不利影响[10]。半球结构的仿真模型如图10所示。

表2 模型材料的基本属性Tab.2 Basic properties of the model material

3.2 抗高过载结构载荷及形变分析计算

根据实际弹载应用环境，此处主要考虑结构在受沿z轴向过载作用时的结构受力，两半球结构保持同轴，载荷约束为z轴方向分别施加4 000g、6 000g、8 000g、10 000g的过载。

内筒支撑轴的后半球与前半球产生撞击作用，可以等效成内筒结构通过后半球对前半球施加等量的载荷力，后半球进行“空腔”处理的体积为π×152×13 mm3，稳定平台质量m=1.2 kg，根据牛顿第二定律F=ma可得，当沿z轴向施加不同过载时，对应的平台结构对后半球施加的载荷力如表3所示。

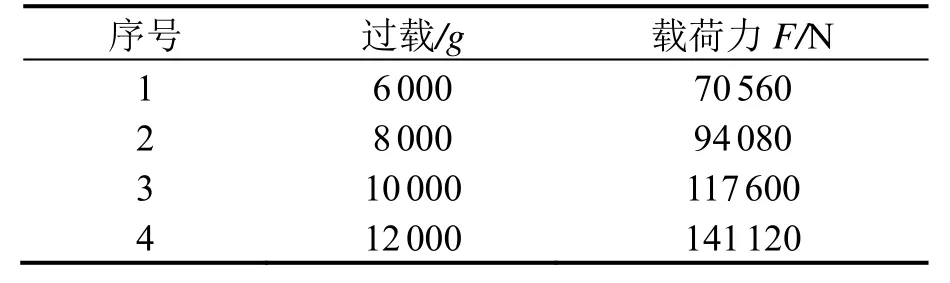
表3 轴向不同过载作用下载荷力分布情况Tab.3 Load distribution under different axial overloads

仿真过程中，通过对平台支撑轴施加不同的载荷力，使得支撑轴前半球对后半球产生相应的过载效果，其后半球形变量分布云图如图11所示。后半球形变量大小可由变形分析得到，如表4所示。

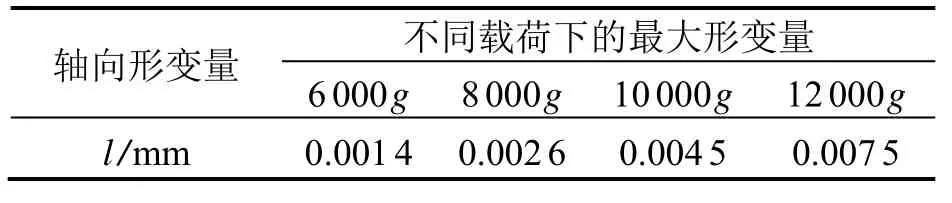
表4 模型结构形变量分析计算结果Tab.4 Results of model structure deformation analysis

由图11和表4可以看出，后半球形变量随着载荷的增大而增大，当施加载荷为12 000g时，后半球最大形变量仅为0.007 5 mm。根据其应力仿真分析，此时的最大应力为2 015 MPa，大于其屈服强度800 MPa，半球会出现塑性形变。

为验证膛内发射后对顶半球在弹丸发动机推送阶段的状态，在上述施加12 000g载荷仿真基础上，再对该结构施加 4 000g的过载，观察对顶半球形变量，如图12所示。

根据材料力学知识相关，工艺热处理后的前半球强度与硬度明显提高，前半球屈服强度可提高至2 000 MPa，远大于后半球，当对顶半球施加载荷为12 000g后再施加4 000g即16 000g过载时，前半球形变量最大为0.015 886 mm，如图13所示。此时前半球虽然也存在一定塑性变形，但形变量较小，可以认为半球基本保持点接触不变。

3.3 仿真结果分析

由以上仿真可知，对顶半球在承受12 000g过载后再承受4 000g过载时总形变量约0.1 mm，该形变量较小。为保证稳定平台的有效工作，轴承结构需要产生相应的正常轴向工作位移。轴承结构通过轴承游隙产生内外圈的相对移动进而产生轴向的位移，保证在冲击载荷下产生一定轴向位移，同时可以使得对顶半在大过载后分离。根据所选轴承型号，轴承正常工作位移为1.6 mm，工作额定载荷为2.4 ～5.4 kN[11]。

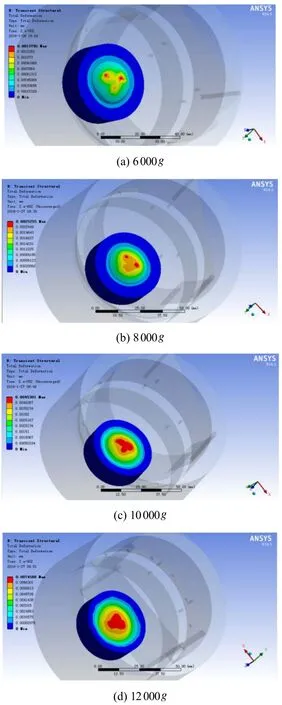
图11 后半球在不同载荷作用下的形变量分布云图Fig.11 Distribution of deformation of the posterior hemisphere under different loads

图12 冲击过载后4 000g作用下后半球形变量Fig.12 Deformation distribution of the posterior hemisphere under the action of 4 000g after shock

图13 16 000g作用下前半球的变形量分布云图Fig.13 Deformation distribution of the front hemisphere under the action of 16 000g

由以上分析可得，轴承结构可产生的最大轴向位移1.6 mm，远大于对顶半球结构的总形变量0.1 mm，所以轴承结构在12 000g过载后继续承受4 000g过载能够正常运转。弹丸惯性飞行阶段最大轴向过载一般不超过10g。平台质量为1.2 kg时，产生的轴向力不超过120 N。在轴承工作额定载荷范围内，飞行过程中可保证相应的弹性，实现过载后两半球分离，满足正常运转形变要求。

4 抗高过载结构性能试验验证

为了验证所优化设计的抗高过载结构的实际抗过载性能，模拟炮射导弹运动过程中所受过载环境，进行了地面马歇特落锤锤击试验。

试验时，将系统固定于马歇特落锤锤头上，将系统上电 100s，保证平台内部传感器处于正常工作状态，设置马歇特落锤齿数，使其对应产生12 000g的冲击过载，再通过设置齿数使其产生相应的4 000g的过载，依次连续完成上述冲击试验，冲击试验现场如图14所示。冲击过载后平台各部件状态如图15所示。

系统在12 000g的冲击后继续4 000g的冲击下内部传感器的输出电压，如图16所示。表5为冲击前后加速度计输出电压值及对应加速度差值，表6为冲击前后陀螺仪输出电压值及对应角速率差值。

图14 冲击试验现场图Fig.14 Impact test site

图15 过载后平台各部件结构状态Fig.15 Structure state of each part of platform after overload

图16 连续冲击过载下MIMU输出电压曲线Fig.16 Output voltage curves of MIMU under continuous impact overload

稳定平台内部安装的三轴加速度计量程均为±10 g，三轴陀螺仪量程均为±400 (°)/s。由表 5～6 可得出，冲击后三轴陀螺仪角速率差值分别为0.009 697 (°)/s、0.007 879 (°)/s、0.014 848 (°)/s，三轴加速度计差值分别为 0.010 138 m/s2、0.005 642 m/s2、0.008 715 m/s2。以上误差都在传感器误差允许范围内，不会对稳定平台参数测量造成影响。

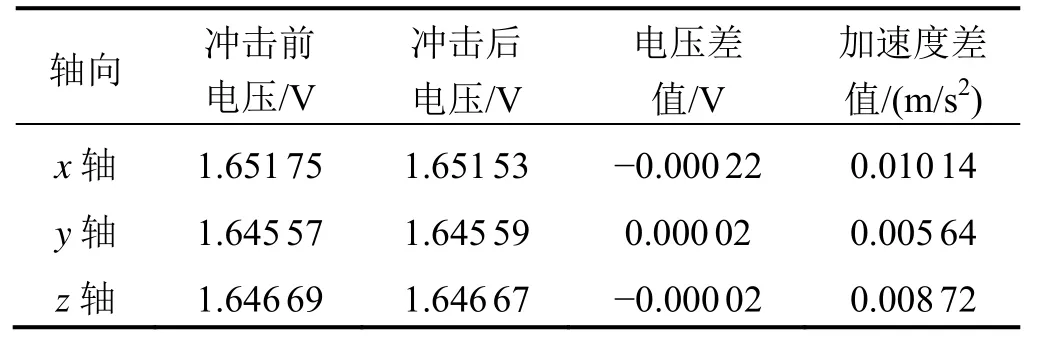
表5 冲击前后加速度计输出比较Tab.5 Comparison on accelerometer outputs before and after impact

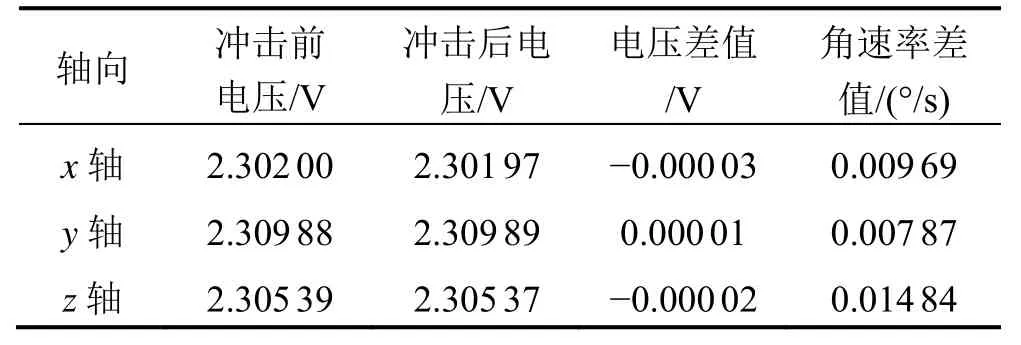
表6 冲击前后陀螺仪输出比较Tab.6 Comparison on gyroscope outputs before and after impact

通过以上结果，试验过后滚转稳定平台内部组件完好，测量对顶半球的总形变，形变量在1 mm以内，轴承结构能正常运转，结构完整，传感器及相关电路电气输出正常，在12 000g冲击后继续4000g冲击下仍能保持正常工作。证明本文所优化设计的抗高过载结构是正确、有效的，能够在连续高过载环境下对滚转稳定平台起到很好的保护作用。

5 结 论

本文对一种基于对顶半球的滚转稳定平台抗高过载结构进行优化设计。对优化设计的“对顶半球”结构进行了力学分析，通过分析计算得出了不同过载情况下“对顶半球”结构所受应力及形变量。通过地面马歇特落锤锤击试验模拟了滚转稳定平台在炮射导弹运动过程中所受高过载情况，仿真及试验结果验证了该抗高过载结构的有效性，该结构在承受12000g的高过载后仍能承受4 000g的过载而不会“机械失效”，为滚转稳定平台创造了稳定可靠的工作环境，为进一步隔离炮射导弹高过载恶劣环境对稳定平台的影响提供了一种有效的优化设计方法。