机载导弹大安装偏差下的快速二次传递对准方法

苏炳志，穆荣军，裴文龙，涂海峰，崔乃刚

（1.哈尔滨工业大学 航天学院，哈尔滨 150001；2.94657部队，九江 332000；3.中国运载火箭技术研究院，北京 100076）

空射导弹作为机载武器的重要力量，具有反应灵活、可快速投入战斗等特点，决定了其在区域战争中发挥着重要作用[1]。动基座传递对准技术作为空射导弹发射前诸元装定的基础，对准精度很大程度上决定了武器系统最终的命中精度。导弹装载在机腹下与机载主惯导之间存在安装偏差，通常假设为小角度（小于 3°）建立线性传递对准模型；然而，在紧急快速响应情况下，由于导弹安装完成后未进行粗校准，弹载子惯导与机载主惯导之间会出现大安装偏差情况[2-3]，在传递对准时直接用主惯导的速度、姿态、位置等导航信息对子惯导进行初始化这一过程引入了大失准角问题，在这种大安装偏差情况下传统的线性传递对准方法不再适用。

针对大失准角传递对准问题，国内外学者[3-7]提出了基于无迹卡尔曼滤波（Unscented Kalman filter，UKF）、容积卡尔曼滤波（Cubature Kalman filter，CKF）、高斯厄米特积分滤波（Gaussian Hermite quadrature filter，GHQF）和粒子滤波（Particle filter，PF）等非线性滤波方法的传递对准方案，但由于非线性传递对准模型复杂、非线性滤波方法计算量大等缺点，目前仍不适宜工程应用；文献[8-9]按时序采用非线性和线性传递对准模型相结合的二次对准方案，尽管减小了一定的计算量，仍不能完全规避非线性传递对准模型的状态估计计算量大等缺点；文献[10]采用将子惯导比力进行坐标系转换的方法，将大失准角问题转化为小失准角问题，但需要预先知道安装偏差角的粗值。

针对上述问题，本文提出了基于双线性模型的快速二次传递对准方法，该方法以一次对准结果为依据旋转主惯导本体系至虚拟过渡坐标系，从根源上消除大失准角，既能适应大安装偏差情况，又具有良好的快速性与精确性。为提高算法实时性，一次传递对准采用降维（9维）线性快速传递对准模型实现主子惯导之间的安装偏差角粗估计；二次传递对准利用一次对准存储在缓存区的数据和惯导实时输出进行对准，采用 12维线性快速传递对准模型估计虚拟过渡坐标系与子惯导本体系之间的安装偏差角及陀螺仪零偏，再结合主惯导本体系至虚拟过渡坐标系的姿态转换矩阵可精确获取主子惯导之间的安装偏差角。以激光主惯导和光纤子惯导为试验对象，开展快速传递对准地面试验，与基于UKF的非线性传递对准方法比较，验证了二次传递对准方法的快速性与精确性。

1 捷联式惯导系统传递对准误差模型

首先给出文中使用的坐标系及其定义：n为导航坐标系（北-天-东系）；a为机载主惯导本体坐标系；a1为机载主惯导虚拟过渡坐标系；b为弹载子惯导本体坐标系； b*为计算弹载子惯导坐标系。

1.1 捷联式惯导系统传递对准非线性误差模型

大失准角下的非线性快速传递对准误差模型[11-12]如式(1)所示：

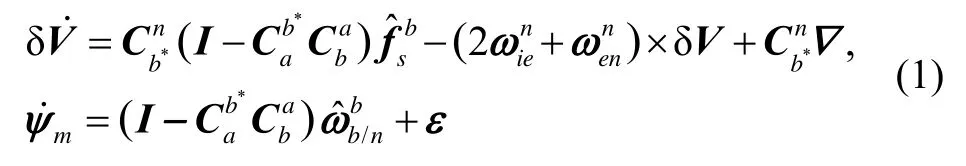
式中，ψax、ψay、ψaz为主子惯导之间的三轴安装偏差角，ψmx、ψmy、ψmz为三轴本体系姿态失准角。

通过对式(1)～(3)的分析，姿态误差方程本质是非线性的，而速度误差方程的非线性是耦合姿态误差方程的非线性引起的。因此只要解决姿态误差方程的非线性问题，即可实现大安装偏差下的传递对准。本文将采用二次传递对准方法通过建立主惯导虚拟过渡坐标系，从根源上解决大安装偏差下的传递对准问题。

1.2 捷联式惯导系统传递对准线性误差模型

在小姿态偏差假设下，sin δ≈δ，cosδ ≈1，对式(2)和(3)进行简化，约去二阶小量（交叉耦合项）后有：

式中，ψa为安装偏差角矢量。

将式(4)(5)代入式(1)，可得小失准角条件下传递对准误差模型：

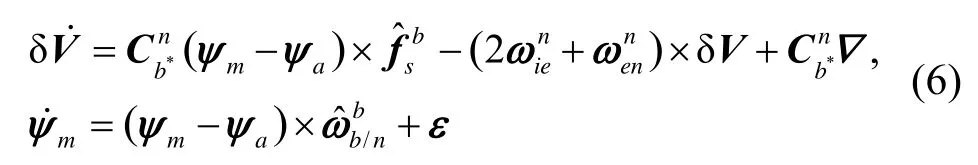
2 基于UKF的非线性传递对准滤波器设计

根据式(1)，综合考虑模型精度与计算实时性，采用“速度+姿态”匹配方式，建立12维非线性快速传递对准模型，采用UKF算法利用滚转姿态激励实现弹载惯导的快速传递对准。

2.1 非线性传递对准状态模型

选取本体系姿态失准角矢量ψm，速度误差矢量δV，子惯导陀螺仪零偏ε和安装偏差角矢量ψa为传递对准状态向量，即：

根据式(1)可得到状态模型微分方程：

2.2 非线性传递对准观测模型

选择速度误差矢量δV和本体系姿态失准角矢量ψm为传递对准观测向量，即：

式中，Vm、Vs分别为主惯导和子惯导的速度矢量，g（·）表示从方向余弦矩阵求取欧拉角的函数，矩阵Cz的定义如下：

2.3 无迹卡尔曼滤波

通常Sigma点的数量选取为2 1n+个，UKF算法的具体步骤如下：

1）时间更新

计算 1k-时刻Sigma样本点：

计算k时刻的一步状态预测：

2）量测更新

计算用于量测更新的Sigma点：

计算 Pxy、 Pyy：

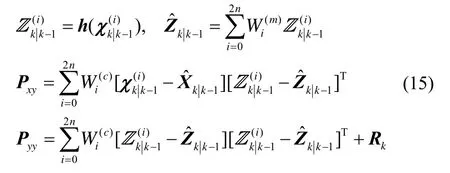
状态估计值为：

3 基于双线性模型的二次传递对准滤波器设计

根据式(6)，综合考虑模型精度与计算实时性，采用“速度+姿态”匹配方式，分别建立9维和12维双线性快速传递对准模型，分两次对准实现对三轴安装偏差角和陀螺仪零偏的估计。

3.1 一次传递对准模型

3.1.1 一次传递对准状态模型

鉴于一次对准时，大安装偏差下的模型线性化误差和交叉耦合项舍去误差对系统的影响远大于陀螺仪零偏的影响，一次对准选取本体系姿态失准角ψmx、ψmy、ψmz，北向、天向与东向速度偏差δVN、δVU、δVE和安装偏差角ψax、ψay、ψaz为传递对准状态向量，即：

由式(6)展开可得到传递对准状态模型微分方程：

3.1.2 一次传递对准观测模型

采用“速度+姿态”匹配观测方式，得到观测向量为：

观测方程为：

式中，H为69×维的观测关系矩阵，V为测量噪声，H矩阵中的非零元素为

3.2 主惯导虚拟过渡坐标系下的姿态输出

过渡坐标系1a至导航系n的姿态转换矩阵

按严格的姿态转换矩阵式(22)将主惯导本体系转换至虚拟过渡坐标系，使虚拟过渡坐标系与子惯导本体系之间满足小角度假设，保证了二次传递对准线性模型的准确性。

3.3 二次传递对准模型

3.3.1 二次传递对准状态模型

二次传递对准状态向量较一次传递对准增加了子惯导陀螺仪零偏即：

由式(6)展开可得到传递对准状态模型微分方程：

3.3.2 二次传递对准观测模型

二次传递对准观测向量与式(19)一致，矩阵 Cz的定义如下：

观测方程的形式与式(20)一致，H为612×维的观测关系矩阵，H矩阵中的非零元素如式(21)所示。

3.4 主、子惯导之间的安装偏差角求取

第二次传递对准估计得到（子惯导本体系b与过渡坐标系 a1之间）的安装偏差角记为则安装偏差阵

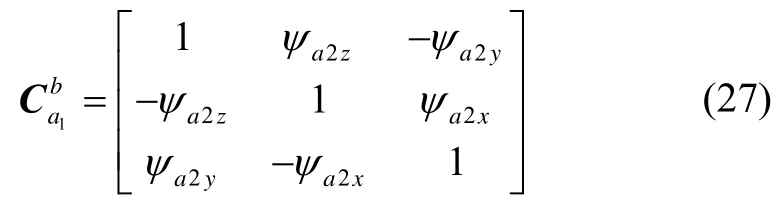
由于式(22)是严格的姿态转换矩阵，而式(27)中的姿态安装偏差角修正量是小角度，因此从式(29)求取得到的主子惯导之间的安装偏差角具有极高的精度。

4 快速传递对准地面试验

4.1 快速传递对准地面试验方案

为了验证基于双线性模型的二次传递对准和基于UKF的非线性传递对准方法，于2017年11月～12月期间在哈尔滨开展了快速传递对准地面试验。地面试验系统组成及主子惯导器件指标如图1所示。

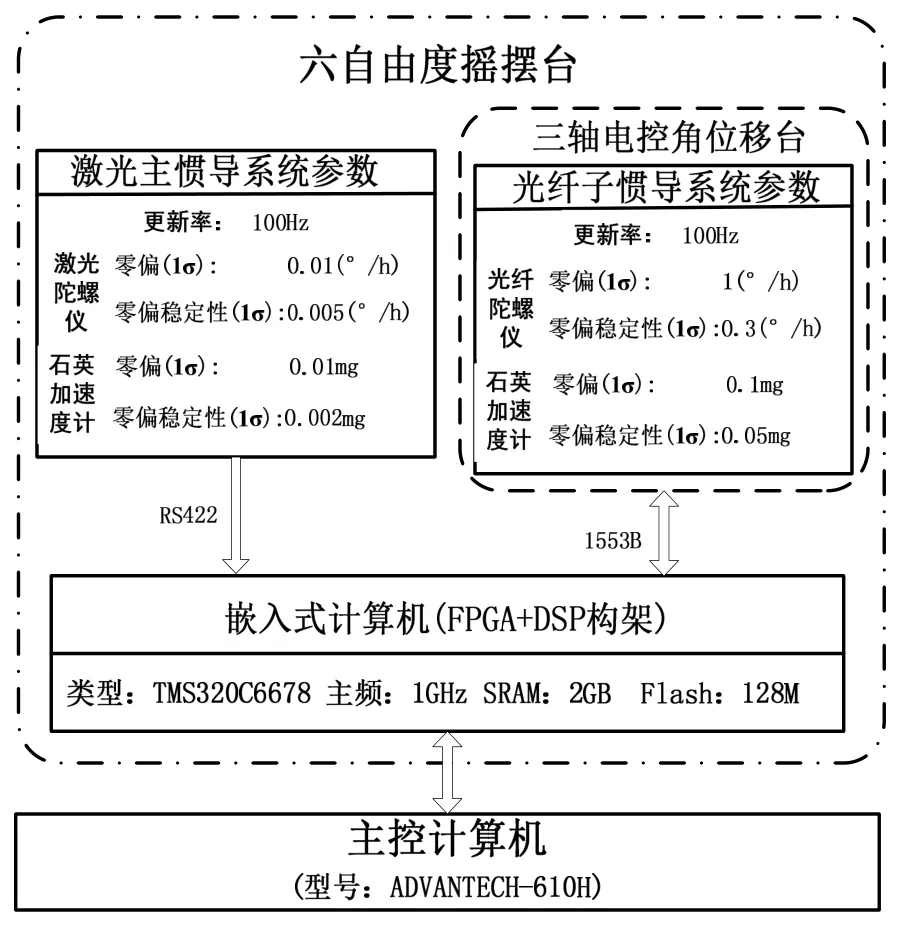
图1 快速传递对准地面试验系统结构Fig.1 Rapid transfer alignment ground test system

为了全面考核与验证所提出算法对安装偏差角估计的正确性，通过三轴电控角位移台改变主子惯导之间的安装偏差角，100次试验三轴安装偏差工况如表1所示。

表1 100次地面试验安装偏差角工况Tab.1 Installation deviation angle of 100 ground tests

为了使系统完全可观测，需载体进行机动，由于摇翼机动对飞机的航向和高度影响很小，常作为快速传递对准算法的机动方案[13-15]；根据对战斗机飞行数据分析和文献[13]的调研，在快速传递对准地面试验对准开始10 s后操作六自由度摇摆台施加幅度10º周期10 s的滚转激励（模拟载机摇翼）；根据文献[15]确定传递对准时间为60 s，传递对准飞行试验的基本时序如图2所示。在基于双线性模型的二次传递对准中，需要申请 1MB内存用于存储主惯导导航数据和子惯导测量数据。

图2 快速传递对准地面试验时序Fig.2 Timeline of rapid transfer alignment ground test

4.2 快速传递对准地面试验结果

基于双线性模型的二次传递对准方法和基于UKF的非线性传递对准方法的地面试验安装角偏差角估计误差曲线与陀螺仪零偏估计误差曲线（表1中典型大安装偏差工况1）分别如图3与图4所示，100次地面试验精度统计结果（对每次对准最后时刻的估计值与“真值”的差进行统计：安装偏差角估计精度通过光学瞄准获取，陀螺仪零偏估计精度通过计算角增量偏差获取）如图 5～7和表 2所示，两种快速传递对准算法在 C6678（1GHz）上每万步计算耗时测试结果如表3所示。

由图3～7和表2～3两种快速传递对准方法的地面试验结果可以看出：一次对准后主子惯导之间的安装偏差角估计精度达到十几角分（线性化误差和交叉耦合偏差的影响），以其为依据将主惯导旋转至虚拟过渡坐标系，极大的减小了误差模型的非线性程度，保证了二次传递对准线性近似模型的准确性；两种快速传递对准方法安装偏差角估计误差收敛曲线与陀螺仪零偏估计误差收敛曲线一致、对准精度相当，水平对准精度 2.5′(3σ)，航向对准精度 1.2′(3σ)，三轴陀螺仪零偏估计精度1.0 (°)/h(3σ)，表明本文所提出的二次传递对准方法能够解决大安装偏差下的对准问题。

图3 快速传递对准安装偏差角估计误差Fig.3 Estimation error of installation deviation angle for rapid transfer alignment

图4 快速传递对准陀螺仪零偏估计误差Fig.4 Estimation error of gyroscopes initial bias for rapid transfer alignment

图5 ψax与εx估计精度统计直方图（100样本）Fig.5 Estimation precision of ψaxandεx(samples: 100)

图7azψ与zε估计精度统计直方图（100样本）Fig.7 Estimation precision of azψandzε(samples: 100)

表2 100次地面试验传递对准统计精度Tab.2 Statistical precision of transfer alignment in 100 ground tests

由图2和表3可知，一次对准结束后，二次对准滤波器开启只需2.76 s（32.76 s二次对准滤算法计算耗时）就能追上当前时标，即二次对准滤波器进入实时计算模式；基于双线性模型的二次传递对准算法较基于 UKF的非线性传递对准算法的计算复杂度降低了70%，极大的减小了弹载计算机的负担。

表3 两种传递对准方法每万步计算耗时对比Tab.3 Comparison on computation times per 104 steps of two transfer alignment method

5 结 论

本文分别建立了地理系下机载动基座传递对准非线性和线性误差模型，提出了一种基于双线性模型的快速二次传递对准方法，能够利用一段数据先后采用两种线性模型进行传递对准，实现大安装偏差情况下三轴安装偏差角和陀螺仪零偏的快速与精确估计。

通过地面试验验证表明，本文所提出的基于双线性模型的快速二次传递对准方法与基于 UKF的非线性传递对准方法相比，对准精度相当，计算复杂度降低了70%，有效解决了机载导弹大安装偏差下传递对准的工程实现性问题。