基于改进步长连续潮流法的电压稳定性分析
2018-12-19谢冬冬潘雪晴刘德仁
谢冬冬,刘 鑫,潘雪晴,刘德仁
(1.国网焦作供电公司,河南 焦作 454000;2.国网河南省电力科学研究院,河南 郑州 450000)
1 连续潮流理论基础
连续潮流法是电压稳定分析的有力工具[1]。主要是指系统从初始潮流解开始,随着负荷的增长,沿P-V曲线对下一潮流解预测、校正,逐步求解系统潮流,直到求得电压稳定极限点的方法,如图1所示。大致可以分为方程参数化、预测环节、步长控制环节、校正环节。
1.1 方程参数化
参数化策略是贯穿整个连续方法的核心,它决定了整个连续潮流的应用情况。主要是想办法构造出1个方程,使得它与常规潮流方程一起构成1个具有n+1个待求变量的n+1维方程组,来确定曲线上的下一个点,其主要的作用就是克服了常规潮流方程在电压稳定分界点处不收敛的问题。

图1 连续潮流法原理
1.2 预测环节
预测环节的目的就是为了给下一步校正环节中计算的准确值提供1个良好的近似初始值,预测环节中得到的近似初值的好坏直接影响到求取精确解所需要的迭代次数,如果预测值与精确解之间的误差较小,那么将需要很少的迭代次数即可找到精确解。
1.3 步长控制环节
步长控制环节是连续潮流算法中重要的一步,选择过大,虽能够提高计算效率,但将造成解的不收敛,选择过小,虽能够找到精确解但却会降低求解的效率。基于此,在选择步长的时候应在初始状态时选择大步长,在接近电压稳定临界点时选择小步长,这样既可以提高求解的效率,又可以确保解的精确度。
1.4 校正环节
校正环节就是根据之前的预测值通过计算来得到实际满足潮流方程的运行点,计算的繁简主要与预测值和真值之间的误差有关。常用的校正方法是牛顿法和近似牛顿法。
2 基于二分法改进步长的原理
无论系统如何复杂,在任意时刻,从系统中某一负荷节点看进去,系统都可以等效为1个电压源经1个阻抗向负荷节点供电的1个单机系统,根据等效后的参数来分析系统的电压稳定性。由于该方法简单易懂,得到了众多学者的广泛研究。这些研究通常假设2个时刻之间戴维南的等值参数没有发生变化,这将增加预测值与真值之间的误差,从而加大计算量。本文基于此,引用文献[2]提出的一种广义戴维南等值原理,并根据求取出来的参数,来选取更接近真值的预测值,从而减少迭代次数,提高计算效率。
2.1 广义戴维南等值原理
线性交流系统中,负荷节点有功功率获得极大值的必要条件是负荷静态阻抗模等于动态等值阻抗模,即|ZS|=|ZLD|。文献[2]进一步将这一结论推广到非线性复变电力系统中。研究简单2节点系统等值电路,如图2所示。

图2 简单2节点系统的等值电路

(1)
负荷静态等值阻抗为
(2)
设电压与电流的函数关系为
(3)
将式(3)带入式(1),可得到RS、XS,根据式(1)—式(3)可得到负荷节点端口电压与电流的关系。负荷吸收的功率为
(4)
设负荷功率因数恒定,有
kPLD-QLD=0
(5)
式中:k为常数。构造拉格朗日函数:
F(Ix,Iy)=PLD+λ(kPLD-QLD)
(6)
式中:λ为拉格朗日常数,将式(4)代入式(6),式(6)中有功功率取得极值的必要条件为
(7)
整理后最终得到:
(8)
即有|ZLD|=|ZS|,负荷静态阻抗模等于动态等值阻抗模。当负荷功率因数不恒定时,可将功率因素约束方程式(5)改写成以下形式:
kPLD-QLD+C=0
(9)
式中:C为常数,令k=0,便是无功功率为恒定值C的情况,对最终的结果并无影响。
综上所述,非线性复变电力系统中,负荷节点获得最大功率的必要条件是负荷静态阻抗模与动态等值阻抗模相等,此时电压临界稳定。
2.2 二分法改进步长的原理
因为在初始稳态时,系统的等值阻抗|ZS|小于负荷等值阻抗|ZLD|,并且二者之间的差值可能较大,通过传统的连续潮流法来精确求取电压稳定临界点则将需要很大的计算量并且步长选择不当还可能会造成不收敛的现象发生。根据上述达到最大功率的必要条件可知,随着负荷的增加,运行点将逐渐靠近临界点,|ZS|逐渐增大,|ZLD|逐渐减小,那么|ZS|与|ZLD|之间的差值将越来越小,那么利用二分法求取二者之间的平均值,从而确定步长,即能减小迭代次数,又能保证预测到的点逐渐靠近极限点。即:
(10)
节点i的预测潮流为
(11)
其中:
(12)
本文通过二分法求取出预测的负荷阻抗值(系统等值阻抗与负荷等值阻抗的平均值)并基于此求取出预测的潮流值,从而确定出一个随系统运行状态变化的步长以保证电力系统的运行方向不断接近电压稳定临界点。因此,当系统运行在初始状态时,与电压稳定临界点之间的距离较远,系统等值阻抗与负荷等值阻抗之间的差值较大,此时确定的步长较大,随着系统运行点逐渐趋近电压稳定临界点,二者差值逐渐减小,从而步长逐渐减小,这样一来实现了变步长控制,可以大大加快求解速度。
3 基于最小等值阻抗变化百分数进一步改进步长的原理
在系统的运行状态逐渐接近电压稳定临界点的过程中,系统等值阻抗不断增加,负荷等值阻抗不断减小,二者之间的差值将逐渐趋近于0,但是当运行点非常接近电压稳定临界点时,单纯的采用二分法来确定步长,很有可能使系统的运行状态越过电压稳定临界点,即系统的等值阻抗大于负荷的等值阻抗,二者之间的差值成为负值,造成潮流方程不收敛,对应的实际系统已发生电压失稳。为解决这一问题,本文提出根据最小阻抗变化百分数来进一步改进步长以精确求取电压稳定临界点。
系统等值阻抗增加百分数为
(13)
式中:|Zi,S(t)|为时刻t对应的系统等值阻抗,|Zi,S(t+1)|为时刻t下一运行点对应的系统等值阻抗。
负荷等值阻抗降低百分数为
(14)
式中:|Zi,LD(t)|为时刻t对应的负荷等值阻抗,|Zi,LD(t+1)|为时刻t下一运行点对应的系统等值阻抗。
那么等值阻抗最小变化百分数为
|ΔZi|=min(|ΔZi,S(t)|,|ΔZi,LD(t)|)
(15)
根据|ΔZi|来预测(t+2)时刻系统的等值阻抗和负荷的等值阻抗分别为
|Zi,S(t+2)|=|Zi,S(t+1)|(1+|ΔZi|)
(16)
|ΔZi,LD(t+2)|=|ΔZi,LD(t+1)|(1-|ΔZi|)
(17)
综上,根据系统等值阻抗增加百分数和负荷等值阻抗减小百分数,确定出等值阻抗最小变化百分数,从而基于最小变化百分数来预测出下一时刻可能的系统等值阻抗和负荷等值阻抗,进而判断出|ΔZi,S(t+2)|和|Zi,LD(t+2)|的大小关系,如果前者大于后者,说明此时已经逼近电压稳定临界点,则只需要进一步减小步长,即可快速精确求出电压稳定临界点。
4 仿真分析
为了验证本文算法正确性以及便于与真实计算结果对比,以IEEE14节点为例,按照文献[2]的功率控制方式进行仿真,仿真结果及分析如下。
对IEEE14节点用本文算法进行详细分析,其中当λmax=1.783时,14节点系统的标准计算结果如表1所示。
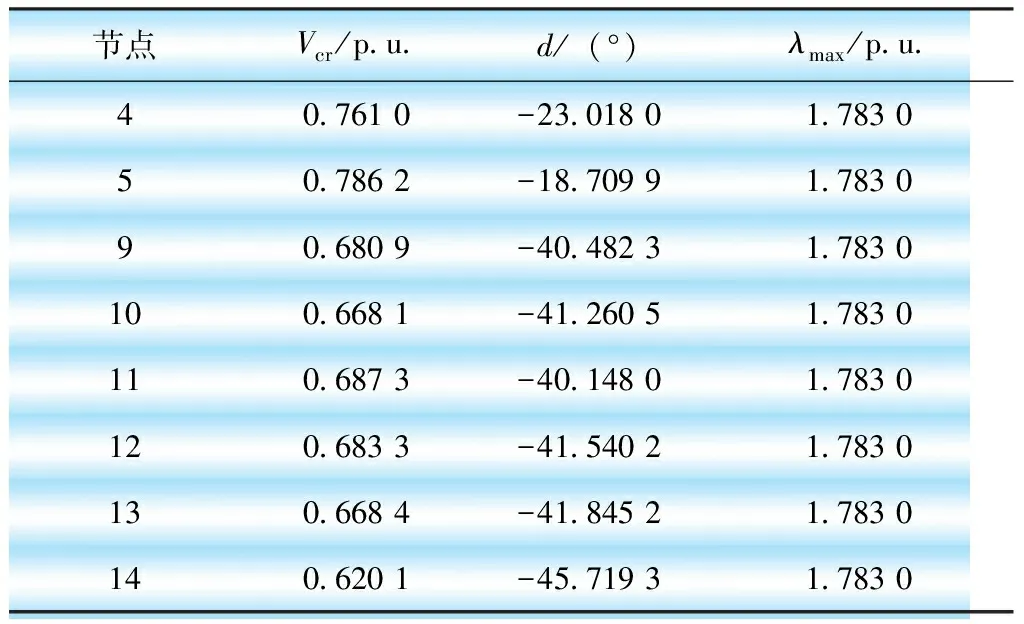
表1 14节点极限潮流标准计算结果
按照本文所提算法,系统潮流预测结果如表2所示,预测效果如图3所示。

表2 14节点系统极限潮流预测结果

图3 负荷节点的电压预测效果
根据仿真结果可知,节点14的电压最低,实际距离电源节点最远,电压稳定性最差;节点5的电压最高,实际距离电源节点的距离最近,电压稳定性最强。本文算法结果与真实结果具有一致性,说明所提理论的正确性。
5 结束语
本文根据系统极大传输功率判据并结合非线性
系统的等值模型,可以快速准确计算系统的临界电压和极限传输功率。仿真结果表明:将电压相量与电流相量展开为电压模的泰勒级数,能够快速准确地求取系统的极限功率和临界电压。
