考虑救援路径拥挤状态的交通应急资源派遣方法

2018-12-18濮居一过秀成

东南大学学报（自然科学版） 2018年6期

濮居一柴干过秀成

(1东南大学交通学院, 南京 210096)(2常州市轨道交通发展有限公司, 常州 213022)

随着高速公路交通运输需求的不断增长,交通应急事件不断发生.特别是重特大交通事故,造成的财产损失和人员伤亡十分严重,需要派遣若干救援点和不同种类的救援资源,以解决路网多事故点与多救援点的救援资源派遣问题.

针对多事故点与多救援点的路网资源派遣问题,对于局部路网且救援资源需求有限的应急事件,只考虑当前应急事件是可行的.但针对大范围路网且常有重特大交通事故发生的状况,救援资源通常是稀缺的.考虑当前和潜在应急事件,是一种基于大范围路网层面进行稀缺资源派遣且考虑派遣稳定性的调度策略.Sherali等[1]建立了经典的基于机会成本的派遣模型.Jotshi等[2]收集路网状况信息,分析当前事件和潜在事件对受灾区域路况的影响,选择可靠路径来调度应急资源.张杰等[3]结合路径行程时间可靠性、路径阻断风险以及路径复杂性等因素,提出了一种基于救援路径选择的多目标规划模型.Chai等[4]改进了基于潜在事故的派遣模型,并给出了求解派遣模型的情景分解法.Zhao等[5]提出救援速度削弱参数,改进了基于潜在事故的派遣模型.Chai等[6]将同等级的事件决策派遣时间和不同类型的救援车辆行驶速度嵌入机会成本中,提出了基于潜在事故的改进派遣模型.赵建东等[7]应用双层规划理论和非合作博弈理论,建立应急车辆调度与再配置模型,以实现对潜在事故的快速响应.

在考虑救援路况方面,曹琦等[8]指出,根据道路状况改进车辆调度方案是需着力解决的突出问题.阎俊爱等[9]采用实时信息与时变信息相结合的方式,估计各路段的行驶速度.李彦瑾等[10]提出基于模糊综合评判的行程时间估算方法,构建面向广义阻抗的网络模型.

救援车辆通过救援路径的行程时间会随着拥挤状态和事件处置进度而发生变化,上述文献中关于救援路径拥挤状态对救援成本的影响涉及较少.本文将考虑应急事件引起交通状态变化的影响,反映救援路径拥挤状态对救援成本的影响,改进应急资源派遣模型,并应用遗传算法求解,获取优化的救援资源派遣方案.

1 传统的交通应急资源派遣模型

针对多事故点与多救援点的路网资源派遣问题,不仅要考虑当前事故的救援成本,还需考虑潜在事故的救援成本.Sherali等[1]提出的传统资源派遣模型如下：

(1)

s.t.

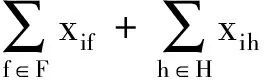
(2)

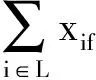
(3)

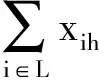
(4)

x∈N

(5)

式中,Z为资源派遣总成本；ri为救援点i配置的救援车辆数；nf为当前事故点f所需的救援车辆数；Ph为潜在事故点h的发生概率；nh为潜在事故点h所需的救援车辆数；λif为救援点i到达当前事故点f的派遣成本；λih为救援点i到达潜在事故点h的派遣成本；xif为从救援点i到当前事故点f派出的救援车辆数；xih为从救援点i到潜在事故点h派出的救援车辆数.

针对λif和λih的计算,文献[4-6]采用救援路径的自由流行程时间作为派遣成本,没有反映救援车辆在救援路径拥挤时的真实行驶状况.

2 改进的交通应急资源派遣模型

本文以网络化交通应急资源派遣为背景,应用垂直排队假设,将救援路径行程时间分为自由流行程时间和排队延误,重新估计救援路径行程时间,以改进传统的应急资源派遣模型.

2.1 救援路径行程时间估计

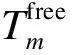
(6)

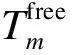
(7)

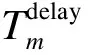
(8)

式中,Cm为路径m的通行能力.

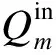
(9)

则

(10)

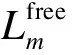
(11)

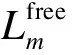
(12)

式中,ξ为平均车辆排队长度因子,一般取为5 m/pcu.

由式(12)反求出tm为

(13)

将式(13)代入式(10)可得

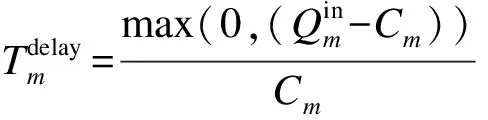
(14)

将式(14)代入式(7)可得

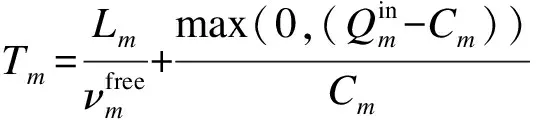
(15)

2.2 模型建立

基于多事故点和多救援点的资源派遣,针对救援点i到达事故点f的多路径选择情况,救援车辆应选择行程时间最短的救援路径,故可得如下约束：

Tif=min{Tifm}m=1,2,3,…

(16)

Tih=min{Tihm}m=1,2,3,…

(17)

式中,Tif为救援点i到达事故点f的最短行程时间；Tifm为救援车由路径m从救援点i到达事故点f的行程时间；Tih为救援点i到达潜在事故点h的最短行程时间；Tihm为救援车由路径m从救援点i到潜在事故点h的行程时间.

将救援车辆行程时间估计表达式嵌入模型(1)中,可得改进的资源派遣模型为

(18)

式中

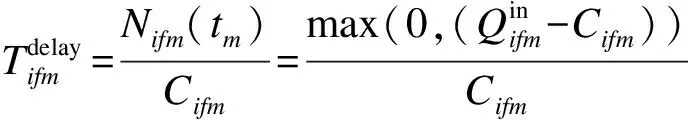
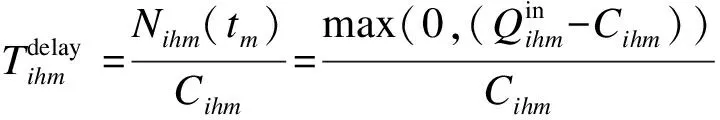
3 示例应用及分析

以河南省高速公路区域路网为背景,应用遗传算法分别对传统和改进派遣模型进行优化求解,揭示救援路径拥挤延误对其行程时间及应急资源派遣方案的影响.

3.1 示例路网网络图及事故信息

示例路网包括京珠、长济、济洛、郑焦、焦温、连霍高速公路,37个节点共包含13个救援点、35个互通点和2个枢纽,如图1所示.其中,节点之间的数字表示两者之间的距离.路网中各节点编号所对应的站点名称见表1.

路网中当前存在7个潜在事故点,各潜在事故点发生事故时对救援车的需求均为1辆.每个救援点配置的救援车见表2.路网当前事故信息和潜在事故信息分别见表3和表4.

3.2 救援路径行程时间估计及比较

根据现场调研,示例路段的通行能力均为2 000 pcu/h,自由流车速为100 km/h.车道数均为3,并且路网中洛常路—焦温、荥阳—郑州西、柏香—沁阳、原武东—原阳、圃田—刘江5条路段为拥挤路段,交通量为2 500 pcu/h,其余路段均设为通畅路段,交通量为1 200 pcu/h.

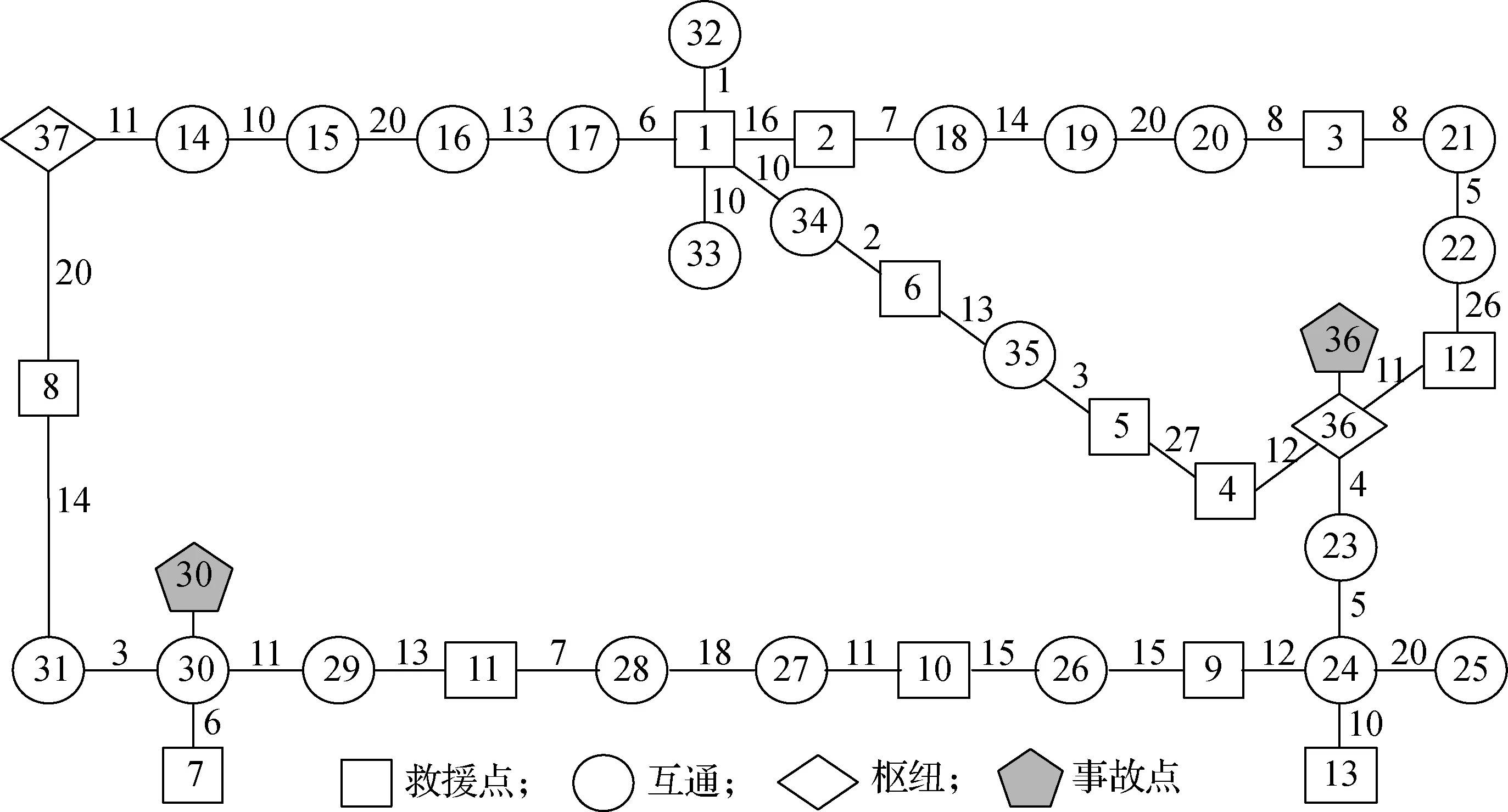
图1 示例路网拓扑结构(单位：km)

表2 救援车辆配置数量表

表3 路网当前事故信息表

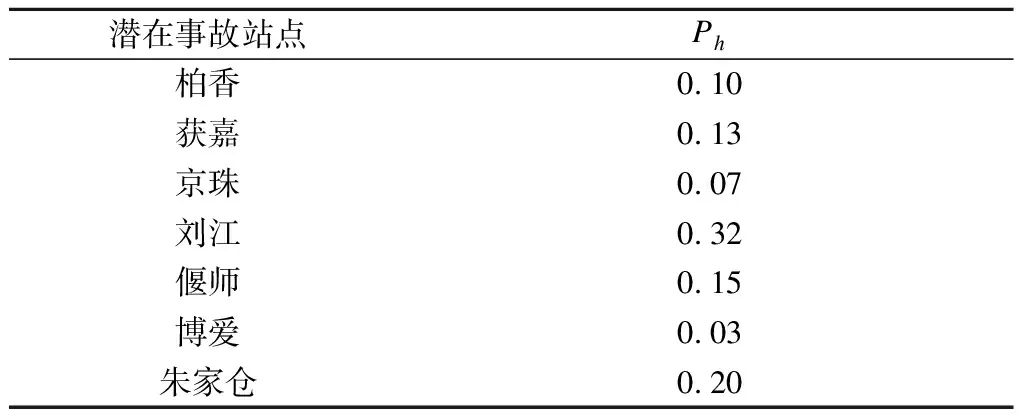
表4 路网潜在事故信息表

由式(6)得到未考虑救援路径拥挤状况的行程时间估计值,由式(15)得到考虑救援路径拥挤状况的行程时间估计值,结果见表5.

根据表5,针对不同模型,各救援点到达事故点的行程时间发生了变化,将其由小到大排列,可得不同模型下各救援车辆行程时间的对比关系,结果见表6.

由表6可知,救援路径未出现拥挤时,2个模型所得行程时间基本相同；发生拥挤时,改进模型(18)所得的行程时间大于传统模型(1).例如,原阳救援点为到达事故点2,在模型(1)下行程时间为8 min,在模型(2)下行程时间增加为30 min,由第2就近救援点变为第5就近救援点.传统模型(1)未考虑事故发生对上游路网交通状况的影响,而改进模型(18)将排队路段行程时间考虑在内,因此,得到的行程时间更接近实际路况.

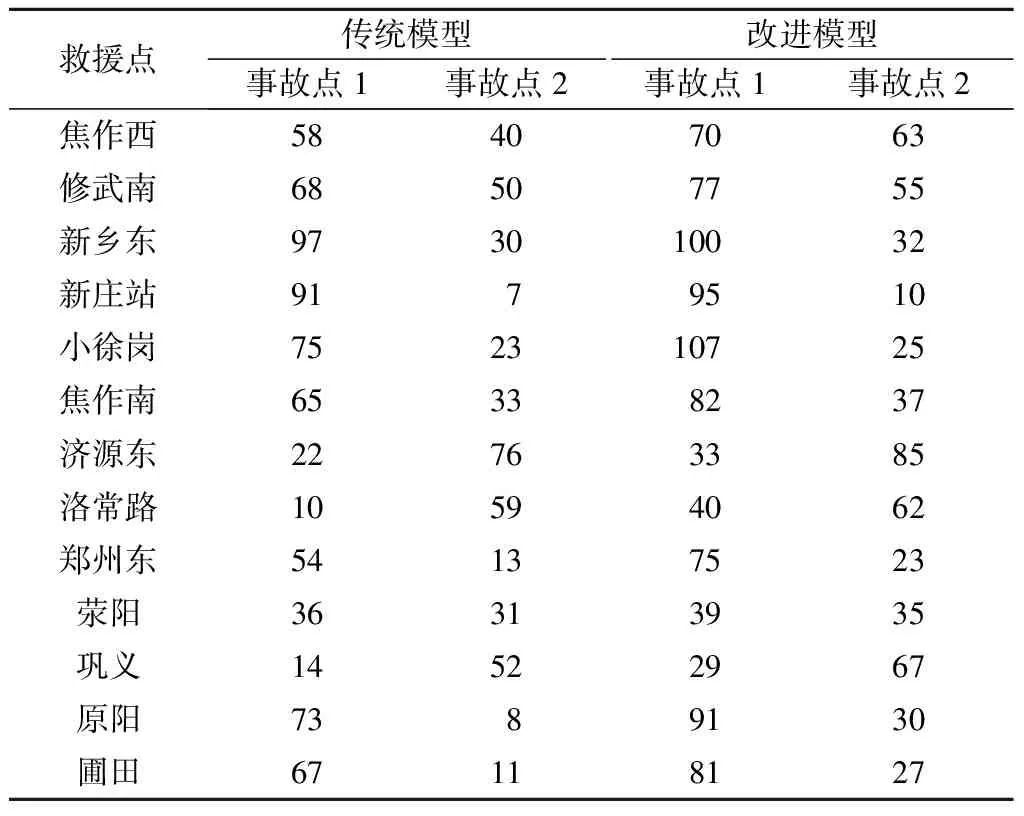
表5 救援车辆的行程时间估计值 min

3.3 基于遗传算法的资源派遣模型优化求解

采用遗传算法进行模型求解,具体计算步骤如下：

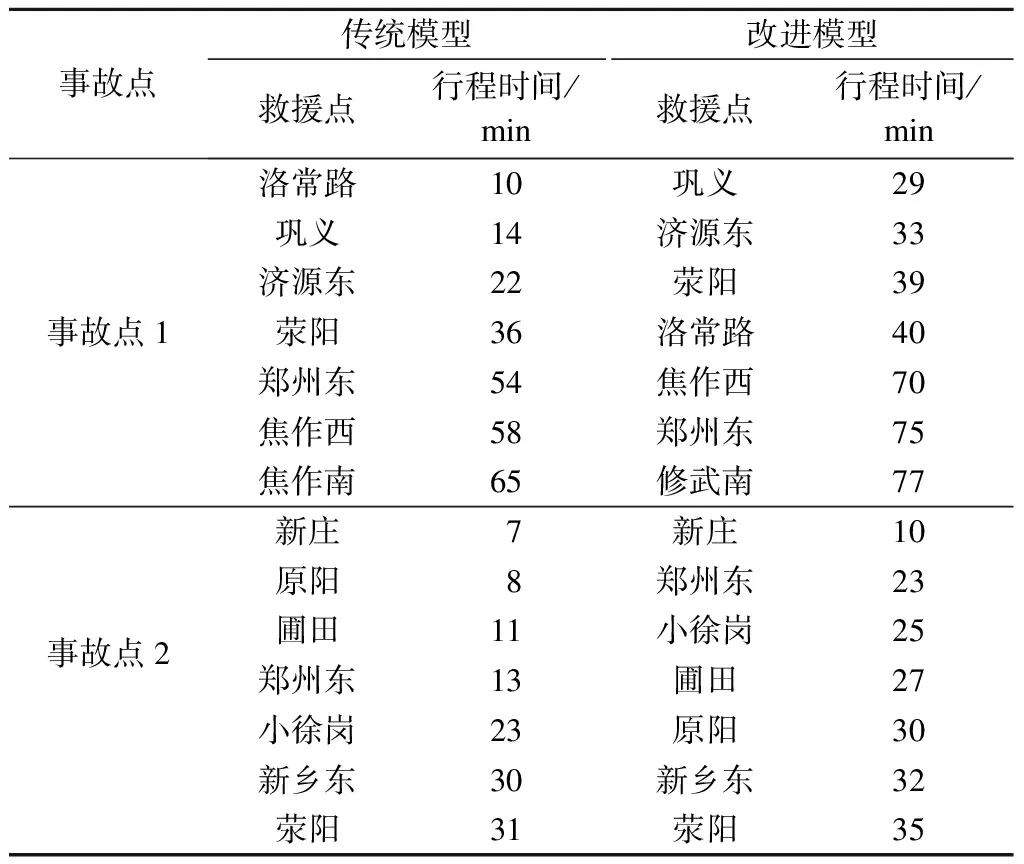
表6 各救援点到达事故点行程时间的相对关系

① 设定遗传算法基本参数,包括种群个数M、最大迭代数tmax、交叉率Pc和变异率PM.

② 编码操作.编码采用实数编码方式,编码长度为决策变量xif和xih的个数,编码值为变量xif和xih的对应值.

③ 生成初始种群.随机情况下产生N个满足约束条件的数据初值,形成初始种群.

④ 计算个体适应度.目标函数在资源有限条件下求解最短救援行程时间,通过惩罚函数法来构造适应度函数,即

(19)

式中,n=1,2,3,…,N.

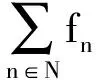
⑥ 交叉操作.采用实数交叉法,对第l个染色体al和第k个染色体ak在j位进行交叉操作的公式为

alj=alj(1-α)+akjα

(20)

akj=akj(1-α)+aljα

(21)

式中,α为[0,1]区间的随机数.根据目标函数约束条件判断个体可行性,若为无效个体,则继续交叉直至生成有效个体.

⑦ 变异操作.采用非均匀变异法,对个体i的第j个基因aij进行变异操作的公式为

(22)

式中,amax,amin分别为基因aij的上界和下界；f(t)=γ(1-t/tmax)2aij,其中γ为随机数,t为当前迭代次数,tmax最大进化次数;β为[0,1]区间的随机数.根据目标函数约束条件判断个体可行性,若为无效个体,则继续变异直至生成有效个体.

⑧ 迭代.若满足最大迭代次数,执行步骤⑨；否则继续迭代,转到步骤④.

⑨ 输出种群中适应度值最高的个体作为问题的最优解.

3.4 算例分析

遗传算法实现环境主要包括编码、选择、交叉、变异、个体适应度评估等模块.设置种群个数为150,交叉率为0.8,变异率为0.1,最大遗传代数为300,代沟为0.8.采用遗传算法对传统和改进的资源派遣模型进行求解,获得的派遣方案对比见表7.表中,T表示救援车辆行程时间；Th表示至事故点的总救援车辆行程时间；Tp表示派遣方案总救援车辆行程时间.

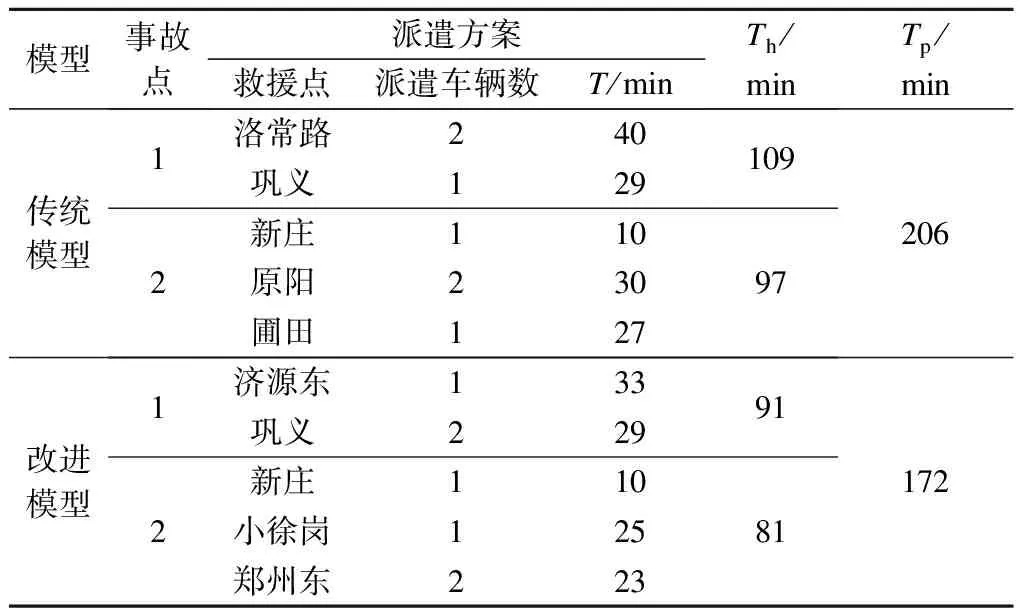
表7 派遣方案对比

由3.2节可知,根据式(15)计算的救援车辆行程时间反映了救援路径拥挤情况,故表7中模型(1)所得的方案仍根据式(15)计算救援车辆行程时间.

根据表7,事故点1的派遣方案分析如下：由于事故1引起路段拥挤,从洛常路派遣的车辆会经过拥挤路段洛常路—焦温,此时若按传统模型所得派遣方案,则会增加救援车辆的行程时间.应用改进模型所得的方案,舍弃从洛常路派遣的救援车辆,改为从济源东派遣,并增加原有巩义救援点的派遣车辆数,则至事故点1的总救援车辆行程时间减少了18 min.

事故点2的派遣方案分析如下：事故2引发各路段产生不同程度的交通拥挤,从原阳、圃田派遣的救援车辆分别会经过拥挤路段原阳—原武东和圃田—刘江.因此,改进模型方案改为从小徐岗和郑州东联合派遣救援车辆,至事故点2的总救援车辆行程时间减少了16 min.

改进模型重新估计行程时间,反映了救援路径拥挤状态,总救援车辆行程时间相对传统模型减少了(206-172)÷206=16.5%,对于多事故点、多救援点的应急资源派遣方案起到了优化作用.