考虑泥皮及径厚比影响的钢混组合桩黏结性能试验研究

2018-12-18冯升明戴国亮钮佳伟龚维明曹小林

东南大学学报（自然科学版） 2018年6期

冯升明戴国亮钮佳伟龚维明曹小林

(东南大学土木工程学院，南京 210096)(东南大学混凝土及预应力混凝土结构教育部重点实验室，南京 210096)

钢管混凝土不仅具有质量可控性高、可受冲击力强、耐疲劳、塑性能力强、耐火性好等优点[1]，并且在施工过程中，可直接使用钢护筒作为模板，还具有施工简单快速等施工优势，在工程中已得到了广泛的应用.

钢管混凝土构件由钢管和核心混凝土2种结构材料组成，其承载性能取决于2种材料在受力过程中的协同作用.钢管与核心混凝土接触面之间的黏结应力使荷载得以进行传递，黏结-滑移性能是钢管混凝土建立起整体承载性能的基础.许多学者对钢管混凝土黏结问题进行了一系列研究，多侧重于对钢管混凝土黏结-滑移性能[2-5]、本构关系[6-7]、剪力件的设置[8-9]等方面，较少涉及因现场施工残留泥皮对其黏结性能的影响.在实际应用中不可避免地会在钢护筒及核心混凝土之间残留少量泥皮，且由于施工要求对于钢护筒径厚比的选择同样影响钢混组合桩的承载性能与变形特性，因此有必要开展泥皮及径厚比对钢混组合桩黏结性能的影响研究.

本文主要在钢管和混凝土之间模拟添加了施工过程中产生的泥皮，并设置了不同径厚比的钢管，采用推出试验(push-out test)，分析泥皮及径厚比对钢混组合桩黏结强度的影响规律，并采用回归分析的方法，给出了考虑泥皮及径厚比影响下钢管混凝土极限黏结强度计算公式，建立了黏结-滑移本构模型及相应的剪切模量计算公式.

1 试验研究

1.1 试验概况

对比试验分为两大类，一类用来研究泥皮的影响，另一类用来研究径厚比的影响.试验制作的试件共计6根，长为450 mm.试件的具体参数见表1.

表1 试验试件参数

为尽可能模拟现场施工环境下钢混组合桩的力学性能，试验采用的试件全部为现场制作，使用的钢管为国标Q235b标准圆钢管，钢管直径均为426 mm，壁厚分别为5与10 mm.钢管的力学性能参数如表2所示.浇筑试件所采用的混凝土为现场浇筑桩基的C60混凝土，配合比如表3所示.试件浇筑采用同批次混凝土，采用相同方式浇筑，并将试件在标准养护条件下养护28 d.制作试件时，对同一批次试件留制150 mm×150 mm×150 mm混凝土材性试块3块，此材性试块与试件同条件养护，用以测定混凝土的力学性能.材性试验的结果如表4所示.根据混凝土材性试验的结果，实测混凝土的立方体抗压强度为62.6 MPa.根据《混凝土结构试验方法标准》(GB 50152—2012)[10]，该混凝土的实测强度等级为C60.纵筋采用16 mm的HRB400热轧螺纹钢筋，箍筋采用10 mm的HPB300热轧光圆钢筋.

表2 钢管材料参数

表3 混凝土配合比

表4 C60混凝土试块材性试验结果

1.2 泥皮制作及混凝土浇筑

泥皮使用现场泥浆制作，泥皮的厚度通过泥浆密度控制.制作薄泥皮所采用的泥浆为第2次清孔时的泥浆，即钢混组合桩现场施工时下放钢筋笼之后清孔时的泥浆，泥浆密度约为1.15 g/mm3；制作厚泥皮所采用的泥浆为第1次清孔时的泥浆，即旋挖机钻孔完毕后孔内的泥浆，泥浆密度约为1.2 g/mm3.

泥皮制作过程将模仿钢混组合桩泥浆护壁水下浇筑混凝土的方式，尽量使制作过程和现场施工接近，具体流程如下：

① 从钢混组合桩现场施工孔内取得泥浆，并将泥浆灌满钢管.

② 采用PVC管进行导流，将准备好的PVC管插入钢管，使PVC管下部距钢管底部有30～50 cm的距离，并将集料漏斗置于PVC管上方，使漏斗口能够卡进管口，同时用塞子将漏斗口堵住.

③ 在集料漏斗内灌满混凝土并快速拔出塞子，使斗内的混凝土全部倒入钢管内，同时将泥浆从钢管管口挤出.

④ 当混凝土灌入而泥浆不再排出时，把PVC管稍微上提，见有大量泥浆流出后接着灌注混凝土.按照这种方法边浇筑边拔管，直到将钢管内灌满混凝土为止，其间轻敲钢管壁以使混凝土均匀分布，浇筑完成后取出部分混凝土，以留出空间便于进行黏结试验加载.

浇筑混凝土时采用同批次混凝土，并制作3块150 mm×150 mm×150 mm的混凝土试块用于之后的混凝土材性试验.推出试验钢管长度为450 mm，混凝土只需浇筑400 mm，留有50 mm的空间用于黏结滑移试验加载.待构件浇筑完毕后与混凝土试块一起在标准养护条件下养护28 d，方可进行承载力试验.

1.3 试验加载方案

采用图1所示的加载装置进行钢混组合桩推出试验，单向进油液压千斤顶，千斤顶标定量程为45 MPa.

本次试验采用液压千斤顶单向分级静力加载.将试件留有50 mm空隙的一端朝下，试验时可有效观察试件内部混凝土的滑移情况.在试件混凝土的表面对称设置2个百分表以相互矫正，并测试钢管与混凝土的相对滑移.加载时预先加载1～2 kN，使仪器与试件之间紧密接触.加载初期，每级加载约为预估极限荷载的1/20，每级荷载加载完毕后维持荷载2～3 min.当混凝土与钢管之间的相对滑移出现非线性增长之后，采用缓慢连续加载，直至试件下端核心混凝土超出钢管底部或者试件已无法继续承担荷载为止.钢管的外表面沿纵向布置应变片，用于研究加载过程中钢管与混凝土的黏结滑移机理.

(a) 推出试验加载方案

(b) 加载试验实际布置照片

1.4 试验过程

试验时每级荷载采用油压千斤顶加载，相对滑移采用百分表测量，钢管应变使用DH3816静态应变采集仪采集.推出试验在试验室加载台上进行，荷载加载分2阶段进行.黏结-滑移破坏过程如图2所示.

加载初期，核心混凝土与钢管之间的相对滑移发展不明显，混凝土顶部所架设的2个百分表的变化均在10-2mm级别；随着竖向荷载的不断增大，钢管与混凝土之间的相对滑移开始变得明显，变化级别在10-1mm级别；当竖向荷载慢慢增大到最大竖向荷载的30%左右时，在加载过程中可听到混凝土与钢管之间滑动时摩擦所发出的“嗞嗞”声，钢管与混凝土之间的胶结力与机械咬合力正在

(a) 最终试验现象

(b) 核心混凝土破坏

衰减；随着竖向荷载增大到最大竖向荷载的50%左右时，试件顶部混凝土表层由于受到摩擦力的作用，出现斜向加剪切裂缝并发生破裂现象；当竖向荷载继续增大至最大竖向荷载的75%附近时，钢管与混凝土之间的相对滑移值迅速变大，伴随有混凝土崩裂的声音；随着竖向荷载继续增大，两者的相对滑移急剧变大，肉眼已清晰可见，竖向荷载已经很难继续加载下去，可认为试件已经破坏.

从试验结果来看，6根试件在推出试验中均表现为延性破坏.从开始滑移到有混凝土崩裂的声音出现，再到相对滑移明显出现非线性直至破坏均没有出现核心混凝土与钢管发生脱离或者破坏后承载力迅速降低的现象.6根试件的破坏现象及黏结-滑移发展特征类似.

2 试验结果分析

2.1 荷载-滑移曲线

黏结破坏荷载定义为黏结-滑移曲线上的拐点所对应的荷载值.文献[11]假定同一截面上的钢管应力分布均匀，混凝土四周与钢管内壁接触处应力分布均匀，以及同一截面四周的黏结应力分布均匀.在受力全过程中，弹性阶段钢管和混凝土的弹性模量分别为Es和Ec，弹塑性及塑性阶段要考虑材料变形的非线性和塑性性质，并推导得到黏结应力τ与相对滑移S的关系式为

(1)

式中，α=As/Ac为钢管混凝土中钢管截面面积As与混凝土截面面积Ac之比；x为不同的横截面位置；n=Es/Ec为钢管与混凝土的弹性模量之比；S为x处钢管与混凝土的相对滑移量.将此关系式进一步化简，设As≈πDnt，Dn为钢管内径,可得

(2)

式(2)即为简化后的钢管混凝土构件推出试验中黏结-滑移本构模型黏结应力τ与相对滑移S的关系式.结合钢管初始应力、黏结初始应力以及相对滑移初始值等边界条件，即可计算得到数值解.之后可将荷载-滑移曲线(P-S曲线)转换成黏结应力-单位长度滑移曲线(τ-s曲线).

由图3可见，各试件的荷载-滑移曲线形态基本一致，在黏结破坏发展的过程中均没有明显的峰值点，曲线上只存在较为明显的拐点.曲线主要分为2个阶段：整体胶结段、滑移摩擦段.当试件处于整体胶结段时，钢管与核心混凝土接触界面没有产生较大的相对滑移，两者之间黏结力钢管与混凝土的黏结应力由化学胶结力、摩擦力和机械咬合力共同承担[12]，且以化学胶结力与机械咬合力为主，曲线基本呈直线上升趋势；当竖向荷载进一步增大，接触面之间的相对滑移开始变大，化学胶结力基本消失，机械咬合力也开始衰减，此时界面黏结力主要由摩擦力和机械咬合力承担，直到钢管与核心混凝土之间的黏结应力达到峰值;之后进入摩擦滑移段，曲线的斜率逐渐减小趋于平缓，滑移量继续增大，荷载增幅减小，此时接触面之间的滑动摩擦力起主要作用.

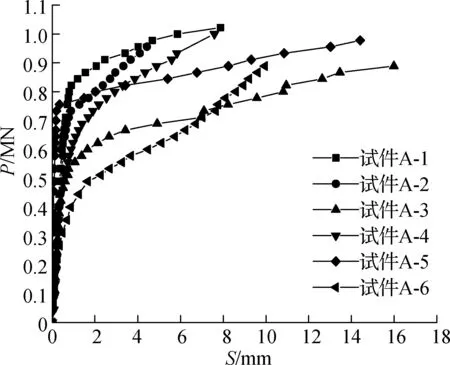
图3 试件荷载-滑移关系曲线

除A-5试件外，各试件从胶结阶段过渡到滑移摩擦阶段的曲线段均较为平缓，可视为延性破坏，A-5试件的两阶段曲线斜率出现突变，属于脆性破坏.A-6试件胶结阶段的特征并不明显，试件的化学胶结力与机械咬合力作用较弱，一开始就出现胶结作用就与摩擦混合的非线性特征.黏结应力-滑移曲线的特征主要取决于界面的摩擦力，即界面的粗糙程度[13].由试件A-5和A-6可见，随泥皮厚度的加大，无论厚径比是否存在差异，都将会对其黏结性能产生影响.

2.2 泥皮对黏结强度的影响

综合表5和图4可看出，相较无泥皮试件A-1，有泥皮试件A-3和A-5的极限黏结强度都出现了不同程度的降低.相较A-1试件的极限黏结强度，试件A-3与试件A-5的极限黏结强度分别低了16%与8%，薄泥皮试件A-3比厚泥皮试件A-5的极限黏结强度甚至低10%，可能的原因是在制作试件过程中无法精确控制泥浆的均匀性，无法将泥皮的厚度定量化，所以试验结果略有误差.但在试件发生黏结破坏之后，各试件黏结应力增长趋势逐渐趋于一致.由此3条黏结-滑移曲线可知，泥皮的存在会大大削弱试件黏结强度，使试件钢管与核心混凝土之间更早发生界面滑移.

表5 各试件黏结破坏荷载及极限黏结强度

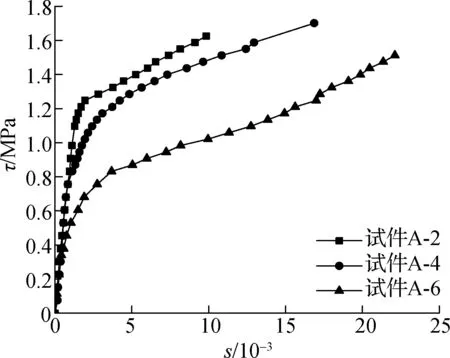
(b) 壁厚10 mm

同时，相较无泥皮试件A-2，有泥皮试件A-4和A-6的极限黏结强度都出现了下降.又由表5中的数据可知其中薄泥皮试件A-4与厚泥皮试件A-6的极限黏结强度分别比无泥皮试件A-2降低了3.2%与27.2%，而厚泥皮试件A-6比薄泥皮试件A-4黏结强度降低24.8%.由此可知，泥皮的存在会削弱试件的黏结强度，破坏试件的界面黏结性能.

综合分析2组对比试验的结果可知，泥皮的存在会大大削弱钢混组合桩的黏结性能，削弱的范围在10～20%之间，但泥皮厚度对极限黏结强度的削弱程度呈不确定性，主要是因为在试件制作过程中无法精确控制泥浆的均匀性.

文献[14]在钢管内表面涂刷防腐蚀层的基础上测得涂刷0.1 mm奈普顿泥浆的钢管复合桩极限黏结强度较未涂刷时强度降低约29%.考虑其为均匀刷涂并事先风干，其结果与本文试验较为接近.

2.3 径厚比对黏结强度的影响

通过对比表5与图5中的τ-s曲线可知，对于本次试验，只有薄泥皮一组试验中随着钢管径厚比增大，钢管混凝土界面间黏结强度降低.试件A-4的极限黏结强度较试件A-3提高3.3%，两者的极限黏结强度比较接近.但在试件发生黏结破坏之后，试件A-4的残余黏结应力要比试件A-3大的多.

无泥皮组黏结强度基本一致，试件A-1的极限黏结强度与试件A-2的极限黏结强度仅相差8%.此组试验中径厚比对试件极限黏结强度影响并不明显.

厚泥皮组试件A-5的极限黏结强度要远大于试件A-6，试件A-5的极限黏结强度相较于试件A-6提高了29.5%.

由3组对比试验的结果分析可知，钢管径厚比分别为42.6和85.2的试件极限黏结强度出现较大离散性.此次试验钢管径厚比对钢管混凝土黏结性能的影响没有明显规律.

一般认为，随着钢管径厚比增大，钢管对混凝土的套箍效应减小，从而导致黏结强度降低[15].根据文献[16]中6组18根钢管混凝土试件的试验结果，径厚比在16.7～34.5间的黏结强度数据离散性较大，认为钢管径厚比对黏结强度的影响并不明显.根据文献[17]中3组9根钢管混凝土构件的试验结果，径厚比39.75相较径厚比35.33的构件同样出现黏结强度增大的现象；文献[18]则认为在径厚比大于50的情况下，黏结强度的减小趋势并不明显.因此,关于径厚比的影响规律仍需进一步确定.

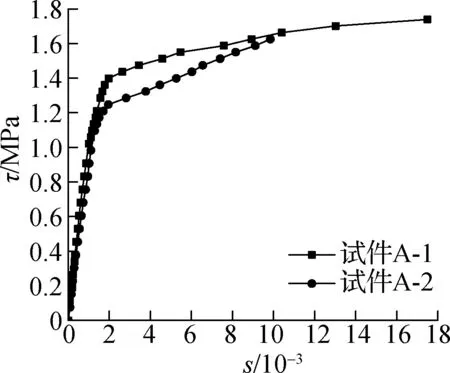
(a) 无泥皮试件

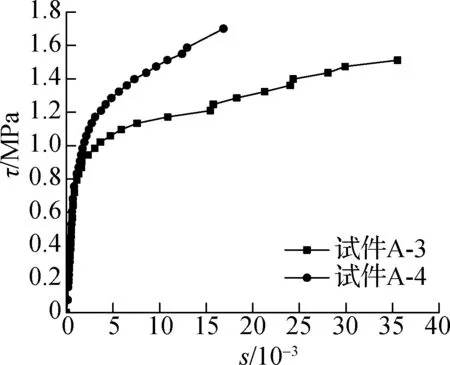
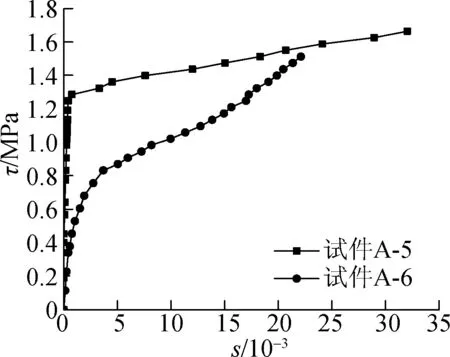
(b) 薄泥皮试件

3 黏结强度

3.1 极限黏结强度计算模型

在推出试验的结果分析中得出了各种因素对钢混组合桩黏结强度的影响规律，为了让结果能够更好地应用于实际工程，对极限黏结强度的主要影响因素进行回归分析.由于泥皮厚度无法量化为数据指标，本文仅考虑泥皮存在对钢管与核心混凝土之间黏结强度的影响.根据试验结果，有泥皮试件极限黏结强度比无泥皮构件极限黏结强度要降低10%～20%，设泥皮影响系数η表示由于泥皮存在对钢管与混凝土界面之间的削弱作用.根据文献[19]总结的黏结强度计算公式形式，将极限黏结强度数据对自变量径厚比(D/t)进行回归分析，综合考虑各项因素后可得到如下回归方程：

(3)

式中,τu为钢管混凝土极限黏结强度；当钢管与核心混凝土接触面无泥皮时η取值为1，当钢管与核心混凝土接触面有泥皮时η取其平均值0.85.

3.2 黏结-滑移本构模型

假定在整个加载过程中，黏结应力沿界面均匀分布，钢管混凝土界面平均黏结应力的计算公式τ与单位长度相对滑移量s分别为

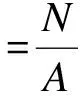
(4)

式中,N为推出试验施加的竖向荷载；A为钢管与核心混凝土接触界面面积；l为钢管与核心混凝土的界面长度.

将所得试件的τ-s曲线中的峰值点或者拐点作为黏结破坏的标志，相应地便可定义钢混组合桩的极限黏结强度：

(5)

式中，Nu为极限竖向荷载.

由图6的τ-s曲线可看出，各试件都存在较为明显的拐点，当黏结应力小于黏结强度时，黏结应力与相对滑移曲线近似为线性关系，当黏结应力大于黏结强度时，黏结应力随着滑移量的增加仍缓慢增长，但增幅较小.因此，可将钢管与核心混凝土之间的平均黏结应力与相对滑移量的本构关系简化为2段斜率不同的双线性模型.第1个直线段斜率较大，线性较陡，应力随单位滑移量增长迅速；第2个直线段斜率较小，线型较为平缓，应力随单位滑移量增长缓慢.简化的关系图如图7所示.

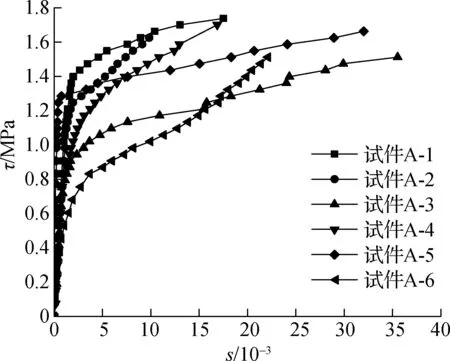
图6 钢混组合桩τ-s曲线

根据简化的τ-s曲线模型，钢混组合桩的黏结-滑移本构关系采用下式表示：

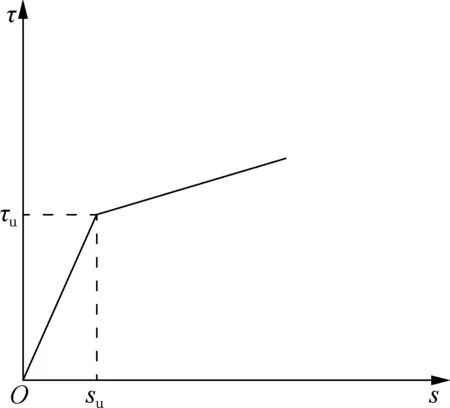
图7 钢混组合桩τ-s简化模型

(6)

式中,Gse为第1阶段黏结-滑移剪切模量；Gsp为第2阶段黏结-滑移剪切模量.

从图6可看出，在整体胶结阶段，所有试件τ-s曲线中直线段的斜率基本一致；但是在进入滑移摩擦阶段后各个试件的由于径厚比与泥皮等因素，开始出现了较大的区别，τ-s曲线的斜率可根据径厚比的区别分为2类，每一类在黏结滑移破坏后表现出的直线斜率基本一致.

根据试验测得数据，逐段对曲线上相邻两点求斜率，取前后两组斜率相差最大的一点作为两阶段分隔点，即τ-s曲线中的峰值点，分别对前后两条曲线进行线性拟合，2条拟合直线的交点作为简化模型的极限黏结强度点，对应的位移为单位长度极限相对滑移量su，2条直线的斜率即为Gse和Gsp，具体拟合出的结果见表6.

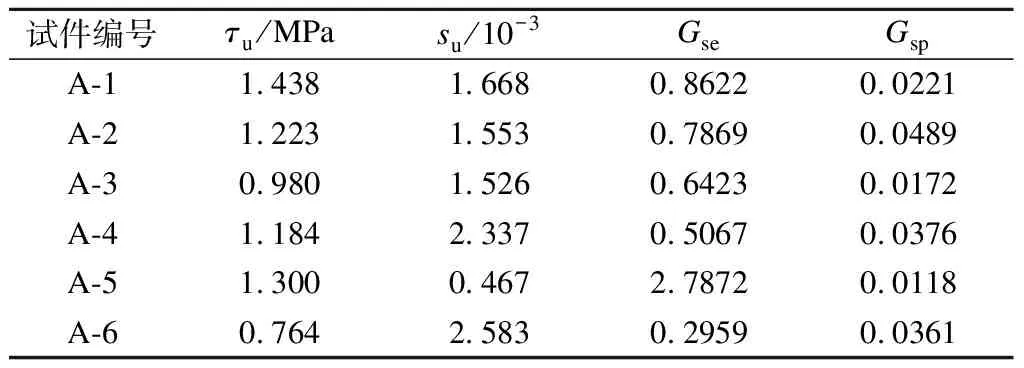
表6 试件简化模型拟合值

由表7及图8可看出，对试验数据拟合后得到的双折线简化模型与原始结果吻合程度较好，计算出的极限黏结强度值相较试验结果误差也较小，最

表7 试件极限黏结强度 MPa

(a) 壁厚5 mm

(b) 壁厚10 mm

大误差也小于20%，具有一定的工程适用性.

Gse与Gsp的取值和泥皮与径厚比2个因素有关，仿照极限黏结强度τu的计算公式,将相关数据进行线性回归分析后可得到以下公式：

(7)

(8)

根据式(6)～(8)计算得到的结果如表8所示.

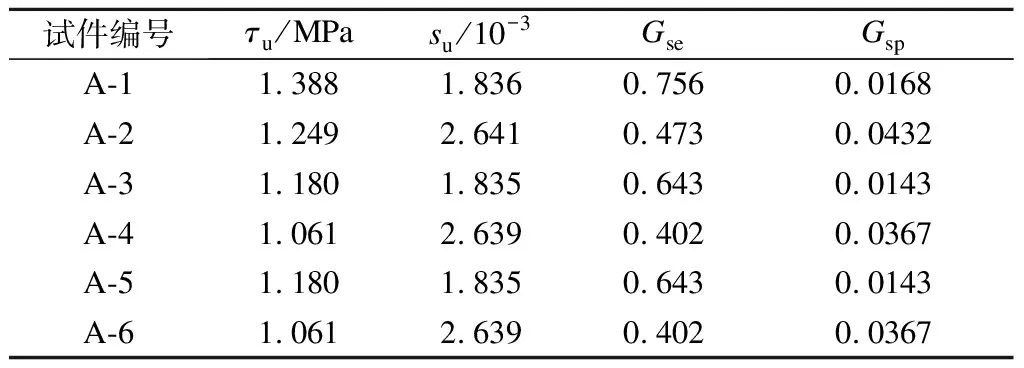
表8 公式计算值

3.3 公式验证

由于将薄泥皮与厚泥皮综合成单一系数进行考虑，因此不同壁厚存在泥皮时简化公式的曲线只有1条.由表9及图9可知，采用本文提出的公式进行估算时，对于不存在泥皮的构件，计算出的极限黏结强度误差较小，τ-s曲线整体吻合比较良好，且比较保守，对工程事先进行判断预估有一定的指导性.当存在泥皮时，计算出的极限黏结强度较试验值较为接近，可用于对试件的事先预估.τ-s曲线在整体胶结阶段，与试验值吻合度尚可接受，但在滑移摩擦阶段，误差较为明显.