铁离子Kα跃迁研究

李文义，胡 峰*，孙 言 ，梅茂飞 ，桑萃萃

（1.徐州工程学院 数学与物理科学学院，江苏 徐州 221018；2.兰州理工大学 理学院，甘肃 兰州 730050）

辐射不透明度是天体物理学一个重要研究内容之一，可以决定恒星的温度结构，也是恒星物理众多重要问题关联因素之一[1]。近年来。辐射不透明度的研究再次受到人们越来越多的关注与重视。不透明度研究计划“Iron Project”是其中重要的研究内容之一，其目的是对铁元素的能级、跃迁特性、碰撞激发、电离等原子数据进行细致研究，力求获得铁元素相关电离态最精细的数据[2]。国内外很多人对类铍的铁离子(Fe XXIII)进行了详细研究，Chidichimo等人利用R矩阵方法计算了主量子数小于4的能级、波长和振子强度[3]。Del Zanna等人用非相对论程序计算了Fe XXIII的振子强度[4]。Charro等人计算了n=2～3之间的Fe XXIII跃迁波长和几率[5]。Landi等人利用组态相互作用计算了Fe XXIII的高阶能级[6]。杨建会等人利用多组态Dirac-Fock(MCDF)方法计算了Fe XXIII的能级、振子强度与跃迁几率，其结果包含真空极化和自能[7]。侯海军等人利用MCDF方法计算了Fe XXIII的Kα和Kβ跃迁[8]。Santos等人计算了 Fe XXIII的 1s22s3p3P0能级的跃迁几率[9]。王凯等人用多体微扰方法计算了Fe XXIII的能级与跃迁几率[10]。EI-Maaref等人用多组态Dirac-Hartree-Fock(MCDHF)方法计算了主量子数小于等于5的能级、波长和振子强度[11]。桑萃萃等人用MCDF方法详细计算了1s2p3能级[12]。

上述提到的理论工作很好的丰富了铁元素的不透明度数据，但是对于本文所要考虑的Kα跃迁，只有侯海军等给出的两条属于1s2s22p-1s22s2Kα跃迁相关信息；同时上述理论工作基本都假设1s电子不参与跃迁，极大限制了Kα跃迁的产生，与所要建立完备的铁元素不透明度数据库不相符合。因此，本文在MCDHF方法和相对论组态相互作用结合的基础上，使用GRASP2K原子结构程序计算拓展了以前的工作，着重探讨类铍铁的Kα 跃迁，详细计算了 1s22s2、1s22s2p、1s22p2、1s2s22p、1s2s2p2和 1s2p3的能级，以及 1s2s22p-1s22s2、1s22p2-1s2p3和 1s22s2p-1s2s2p2三种 Kα 跃迁系，以达到填补数据空白和提供数据验证目的。

1 波函数和能级的计算

本文所用的多组态Dirac-Fock理论(MCDF)方法在文献[13-14]中已有详细描述，这里仅作简单的介绍。在多组态Dirac-Fock理论中，一个核电荷数为Z、具有N个电子的原子或离子体系的Dirac-Coulomb哈密顿量为(原子单位)

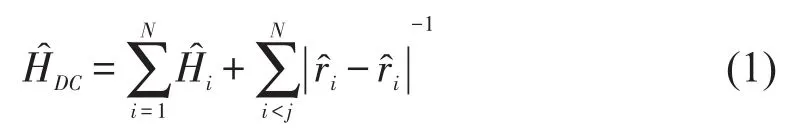
中心场近似下单电子的旋轨波函数可表示为

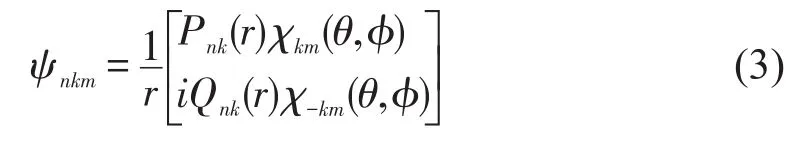
式中k为Dirac量子数，Prk(r)和Qnk(r)分别为相对论径向波函数的大小分量，χkm为自旋函数。

N电子体系的组态波函数是所有单电子旋-轨波函数组成的N阶Slater行列式波函数的线性组合，即

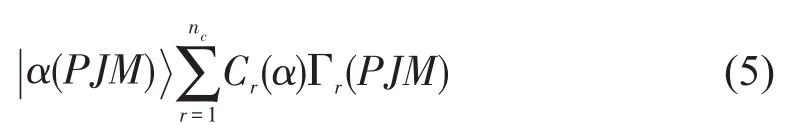
式中nc是组态波函数的个数，Cr(α)为组态混合系数。

对角化由原子波函数(5)式构造的哈密顿矩阵，则可得到相关原子态的能量和组态混合系数。对于其他高阶效应，如Breit修正和主要的量子电动力学QED效应，可作为微扰处理。

2 修正效应

Breit相互作用来源于一个横向光子发生交换而引起两个电子间库仑相互作用的修正，对于高离化态原子，Breit相互作用对原子的精细结构的影响能达到10-6。在本文的计算中，Breit相互作用的贡献是作为一阶微扰来考虑的。量子动力学（QED）效应来源于电子-正电子的运动，其电磁场能产生辐射修正，包含自能和真空极化两部分，自能占主要部分。为简化计算，考虑真空极化时只研究Uehling势的影响。为了得到能量和波函数的高阶近似值，需要考虑Breit修正和QED修正。

3 结果与讨论

3.1 能级

原子结构计算需要考虑两个因素，计算精度和计算经济性。所谓计算经济性就是要统筹考虑计算的收敛性和程序本身的计算能力。因此在本计算中，需要通过对主量子数和轨道角量子数数目扩展数目进行限制。本文考虑了n=1～4的所有轨道以及 5s、5p、5d、5f等轨道，同时通过计算发现加入5g轨道会造成计算结果不收敛，因此计算中不考虑5g轨道的作用。尽管对主量子数和角量子数进行了限制，计算的结果仍然可信的。表1给出了当前MCDHF方法的计算结果。从表1看出，属于QED效应的真空极化和自能的贡献较小，与文献[14]结果一致。同一组态，不同谱项之间的真空极化和自能数值相差不大。Breit贡献趋势不明显，数值上基本和自能一个量级。其中1s2p3的5S2受组态混合的影响，其能级值明显低于1s2p3的其他能级值。为了再次验证当前计算的准确性，我们在图1中比较了Fe XXIII最低2个组态即1s22s2p和1s22p2的9个能级，实验值[15]来自于美国国家标准技术与研究院（national institute of standards and technology，NIST），理论计算值分别取自EI-Maaref等人的计算结果[11],以及原子与分子数据库(atomic database for spectroscopic diagnostics of astrophysical plasmas,CHIANTI)[16]和顾明峰用组态相互作用与多体微扰相结合的计算结果[17]。从图1可以看出，当前计算值与实验值偏差在0.1 eV，要好于EI-Maaref等人的计算结果和CHIANTI的计算值。

3.2 波长

辨识发射谱是低密度等离子体诊断很好的手段，因此波长的精确测量对于研究等离子体状态是必不可少的。由于Kα跃迁的复杂性，其波长小区域内相互重合，不易区分，使得实验观察较为困难。到目前为止，实验只能观测到13条Kα跃迁谱线。从表2可以看出，当前计算值与实验测量值偏差在-0.000 2～0.000 4 nm之间，能够很好地说明当前计算的准确性。同时图2和3给出了1s22s2p-1s2s2p2和1s22p2-1s2p3Kα跃迁所有波长值。图1和图2纵坐标值，来源于跃迁几率在库伦规范和哥伦布规范中表示值的比值。文献[14]指出当库伦规范和哥伦布规范中比值越是接近于1，其计算结果越是准确。从图1和图2，当前两种规范比值基本接近于1，也有部份比值偏差较大，这可能是由于组态混合不易区分引起的。

表1 类 Be的铁离子能级/eV（a（b）=a×10b）

3.3 能级寿命

能级j的能级寿命τ可以表示为：

能级寿命作为一个可被测量的量，可用来检验理论计算的准确性。因此，表3给出了1s22s2p和1s22p2的部分能级寿命。其中1s22s2p3P1实验值来自Hutton等人用光束-薄膜测量技术给出的数据[18]，1s22p2的实验值来自于Buchet采用同种测量技术给出的数据[19]。理论值由王凯等人用多体微扰方法和组态相互作用相结合的方法计算的结果[10]。从表3可以看出，当前计算结果与王凯等人结果相吻合。但2s2p3P1计算值明显偏大，因此需要其他理论计算结果来验证或者重新测量修正实验值。

图1 1s22s2p和1s22p2理论计算值与实验值的比较

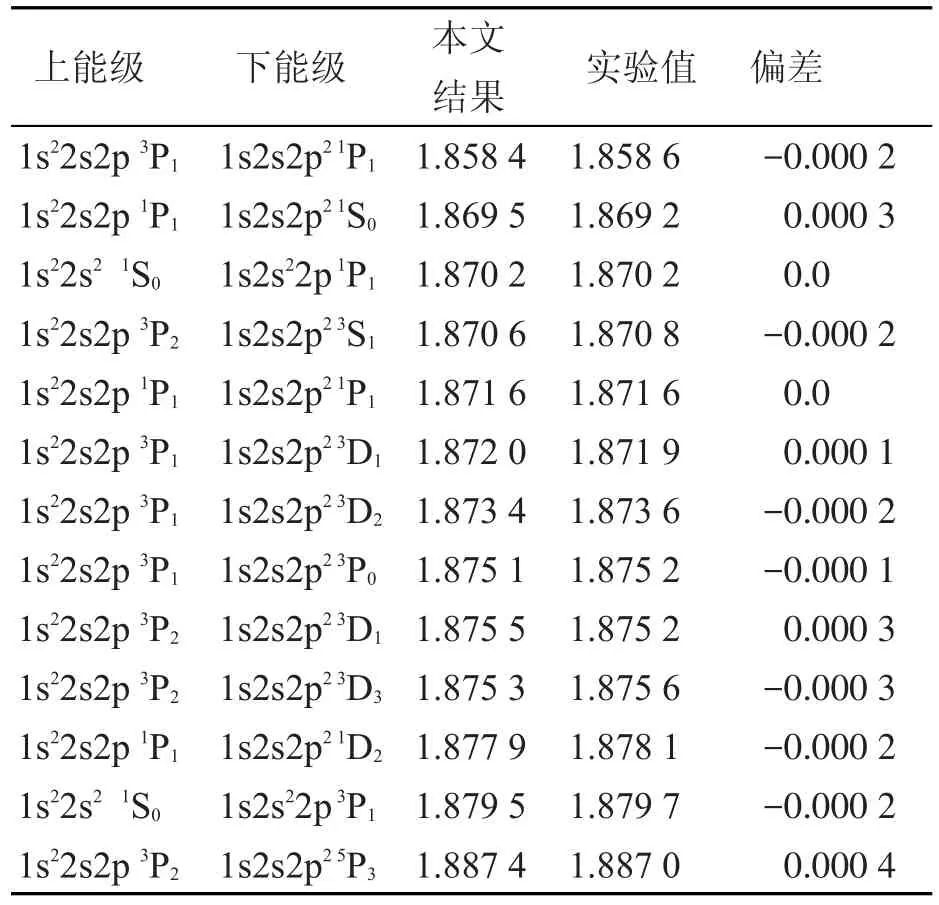
表2 类Be的Kα跃迁波长理论值与实验值比较(0.1 nm)

4 小结

图2 1s22s2p-1s2s2p2Kα跃迁波长

图3 1s22p2-1s2p3Kα跃迁波长

表3 类Be的铁离子的能级寿命/ns

本文利用MCDHF方法详细计算了Fe XXIII Kα跃迁的能级、波长和跃迁几率，MCDHF的结果与已有的理论和实验结果相一致。这些结果对于填补类Be离子的Kα跃迁的空白有重要的意义，同时对于将来辨识谱线和获取等离子体状态信息也有重要的意义。当前计算值是在重点考虑属于Kα跃迁组态基础上给出的，其部分计算结果仍有提升的空间。因此在今后的计算中，需要考虑更多的能级、组态混合以获得更好的结果。