计算机辅助破解数列不等式——从2013年广东理科第19题想到的

（吉林省通化市第一中学 吉林通化 134000）

当今社会，教育现代化手段越来越多，越来越丰富，现代教育技术与数学学科教育教学整合是呈现在新形势下教学改革的一个重要问题。在我们的高中数学教育教学中，如何通过网络和多媒体以及手机IPAD等等现代化教学手段进行数学演练实验，如何改变传统的数学教学模式，优化教学教育思维过程，推动教学方法的改进升级，从而提高学习效率，帮助学生更好地获得知识和提高应用应变思维能力，这是我们数学教育工作者在数学教学中经常应该思考的问题。[1]

比较其他学科的知识，数学知识逻辑性强，易量化，易数字化，这为现代教育技术与中学数学课程的整合提供了必要的条件，几何画板等等现代教育软件的应用普及都有利于数学应用事业的发展。现代教育技术与中学数学课程的整合，将有利于营造新型的学习型社会，营造全方位的学习环境；将对中学数学课程的各个组成部分产生变革影响和作用；将带来课程实施的变革；将有助于课程评价的变革与改善；更重要的是将带来学习方式的革命，为新一轮课改推波助澜。[2]

今天研究一个简单的小例子，最近做了2013年广东理第19题如下：

[解析]

（1）直接将n 换为2代入递推式求解；

【学科网考点定位】本题考查数列的通项公式和数列求和问题，以及不等式的证明。在第三问证明中，大家看到把第一项和第二项不动，从第三项开始放缩处理，很是艺术；若提前一项结果就错了，导致放缩变大而失败。

最近我看见一个类似的题：

通过上题的分析，应该前几项不动，后面进行放缩，可是留几项呢，这就得试验了；

经试验，保留前10项，从第11项开始放缩，证明完毕；

在此，我想如果右侧常数又变换了怎么办呢：所以我决定用计算机程序语言设计一个程序来证明：

我先用QBASIC语言证明：循环结构中嵌套一个选择结构即可见下图。

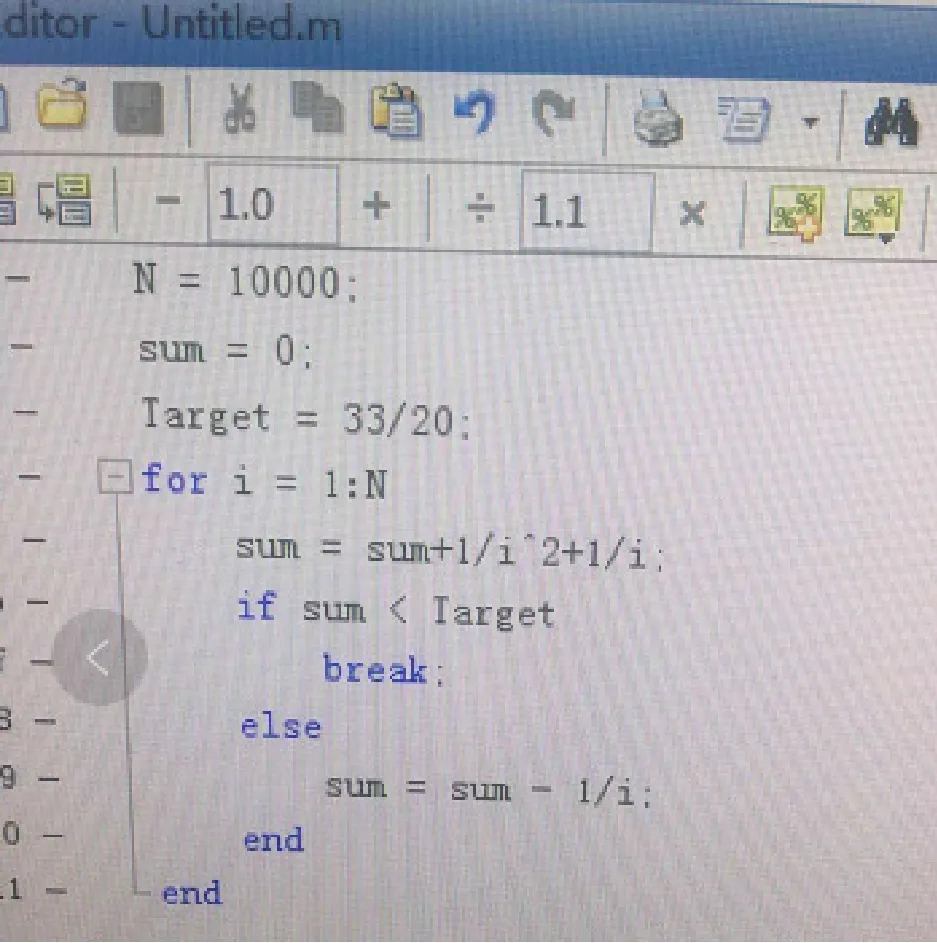
再来高级些的，见右图。

运行结果都可以得出：留10项，之后进行放缩即可；

这样，右侧的数据再变化，只要调整一下数据，瞬间就可以出结果；此类问题轻松被这个程序段秒杀。

仅仅举一个例子，抛砖引玉，研究还要继续，希望更多的人能用计算机解决更多的问题