渗流圆的等效原则

2018-12-18李传亮邓鹏朱苏阳刘东华

新疆石油地质 2018年6期

李传亮，邓鹏，朱苏阳，刘东华

（1.西南石油大学石油与天然气工程学院，成都 610599；2.中海石油（中国）有限公司湛江分公司，广东湛江 524057）

油气水在地层中的流动与电流在导体中的流动类似，描述渗流的达西定律与描述电流的欧姆定律也具有相同的形式，根据电学原理研究渗流力学问题，即水电相似原理[1]。等值渗流阻力法是渗流力学和油藏工程的常用方法[2-3]，是根据水电相似原理建立起来的一种等效方法，是欧姆定律在渗流力学中的应用。由于该方法简单且直观，因此，在石油工程领域得到了广泛应用，以解决复杂的渗流问题[4-7]。等值渗流阻力法包括线性流和径向流两种基本流动形态的等效处理。线性流的等效处理较为简单，实际应用中基本没有分歧。但是，对于径向流的等效处理却一直存在不同观点，主要是对渗流圆的等效原则有不同的理解，等效后的渗流圆有大、小之分，因此，等效后的渗流阻力和油井产量公式便存在差别，计算的油井产量也不同。为更好地使用等值渗流阻力法解决渗流力学问题，必须对渗流圆的等效原则加以明确，只有统一了等效原则，才能得到相同的等效结果。

1 径向流与线性流

若一口直井位于圆形地层的中心（图1），如不考虑地层伤害，油井的产量（地层的流量）公式[8]为

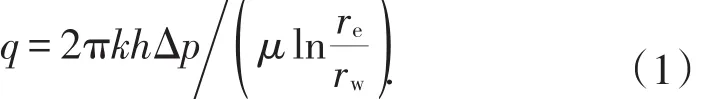
图1 圆形地层直井渗流示意

径向流的所有流线，都沿着圆形地层的径向线指向圆心（图1），也就是一个渗流圆。把径向流的产量公式（1）式写成欧姆定律的形式，则为

由（1）式和（2）式，得径向渗流阻力：

若地层为一线性地层，流线为一组平行线（图2），此即线性流，地层的流量[8]为

图2 线性地层渗流示意

把（4）式写成欧姆定律的形式，则为

由（4）式和（5）式，得线性流的渗流阻力为

2 简单渗流区域形状

实际地层通常不是圆形或线性地层，而是不规则的形状，流线也往往不是平行线和径向线，更多时候是弯曲的曲线，这种情况下的产量公式很难给出。但是，前人想到了一种近似处理方法，即把不规则的渗流区域形状等效成圆形或线性地层，这样就可以方便地给出油井的产量公式。

图3为一个正方形地层，正方形的边长为a，渗流区域的面积为a2，直井位于正方形的中心，若把它等效成图1的渗流圆，有两种等效处理方法。

图3 正方形渗流区域

第一种等效处理方法就是面积等效，让正方形与圆形的面积相等，则等效渗流圆的半径为

第二种等效处理方法就是周长等效，让正方形与圆形的周长相等，则等效渗流圆的半径为

很显然，用周长等效法得到的渗流圆是大渗流圆，用面积等效法得到的渗流圆是小渗流圆，因此，计算的产量自然有所不同。

对于复杂的任意渗流区域形状，前人通过严格的解析方法，给出了一个统一的等效公式[9]，即

对于正方形地层，CA=30.9，代入（9）式，得re=0.57a，与面积等效法得到的小渗流圆十分接近，即小渗流圆在理论上更合理一些，而大渗流圆则高估了渗流阻力，低估了油井产量。

3 复杂渗流区域形状

封闭边界的任意泄油区域形状的等效问题，通过（9）式基本上都能解决。但是，若地层存在部分开放边界或定压边界，（9）式就无能为力了，这时必须进行分区等效。

3.1 线性流—径向流组合

排状注水开发井网的复杂渗流，可以分解成多个渗流单元，每一个单元的渗流都相同，研究其中的一个单元即可。图4为排状注水开发井网的基本渗流单元，单元两侧的封闭边界为开发井网的分流线，两端的定压边界代表注水井排。由其流线分布可以看出，远离油井区域的流线近乎平行，可以用线性流进行等效；而近井区的流线向井底汇聚，可以用径向流进行等效。因此，整个流动可分解为两个线性流和一个径向流。

径向流的渗流圆可以采用两种方法加以确定，一种方法是让渗流圆的直径与地层的宽度相等（图5），即直径等效法，等效后的渗流圆为大渗流圆，渗流圆半径为

图4 排状注水开发井网基本渗流单元

图5 排状注水开发井网直径等效法等效渗流单元（大渗流圆）

渗流圆的渗流阻力为

线性流由左右两个完全相等的部分并联组成，其渗流阻力为

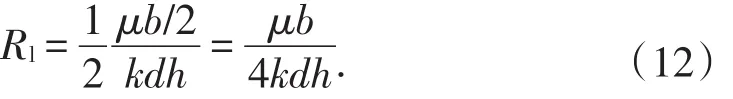
由于地层的长度远大于渗流圆的半径，因此（12）式忽略了渗流圆对线性流的影响。地层总的渗流阻力为

按照欧姆定律，油井的产量公式为

另外一种处理方法，是让渗流圆的周长与地层的宽度相等（图6），即周长等效法，等效后的渗流圆为小渗流圆，渗流圆半径为

图6 排状注水开发井网周长等效法等效渗流单元（小渗流圆）

油井的产量公式为

（14）式与（16）式的唯一不同就是分母上差了一个π，大渗流圆的渗流阻力偏大，油井产量就相应地偏小。实际工作中大都采用周长等效法，但是，哪一种更为合理，需要用后面的径向流—径向流组合加以证明。

3.2 径向流—径向流组合

图7 圆形地层环状井网

在圆形地层中布置一个环形井排，井排半径为rp，油井数为n（图7），环形井排的供给半径为re.求解环形井排的生产问题，与求解扇形地层等分线上一口直井的生产问题完全相同。

图7中扇形地层中的渗流包括两个径向流，一个是从供给边界到生产井排的径向流（外部径向流），另一个是从生产井排到油井的径向流（内部径向流）。外部径向流不需要等效处理，其渗流阻力称作外阻，外阻的大小为

内部径向流有两种等效处理方法，一种方法是让渗流圆的直径与扇形地层井排的弧长相等，即直径等效法，等效后的渗流圆为大渗流圆，渗流圆半径为

内部渗流圆的阻力称作内阻，内阻的大小为

渗流总阻力为

于是，按照欧姆定律得油井的产量公式为

另一种处理方法是让渗流圆的周长与扇形地层井排的弧长相等，即周长等效法，等效后的渗流圆为小渗流圆，渗流圆半径为

油井的产量公式为

（21）式与（23）式的唯一不同，就是分母上差了一个π.（23）式在渗流力学中利用保角变换进行了严格的理论证明[10]，因此具有一定的理论合理性，而（21）式则没有经过理论上的证明。换言之，小渗流圆比大渗流圆更加合理。

4 水平井的情况

图8 圆形地层水平井渗流

若在圆形地层中心打一口水平井，则地层中的流动既不是径向流，也不是线性流，而具有复杂的流动形态（图8）。

图10 水平井近井区的径向流

求解水平井的渗流，可以把图8中的复杂渗流简化成远井区的径向流（外部渗流圆，图9）和近井区的径向流（内部渗流圆，图10）两部分，地层的渗流阻力也由外阻和内阻两部分组成。

关于图10中内部渗流圆的等效处理结果也有大渗流圆和小渗流圆之分。大渗流圆的等效方法是让渗流圆的直径等于地层的厚度（直径等效法），小渗流圆的等效方法是让渗流圆的周长等于地层的厚度（周长等效法）。这两种处理方法与图5和图6中直井的等效处理方法类似，只是把地层的宽度变成了图10中的地层厚度。

许多水平井的产量公式都采用了小渗流圆的等效处理方法，如Borisov公式、Giger-Resis-Jourdan公式、Renard-Dupuy公式。

Borisov公式[11]：

采用大渗流圆进行等效处理的水平井产量公式较少，主要有Joshi公式和陈元千公式。Joshi公式[14]：

（27）式与（26）式只在分母上相差一个π.

陈元千公式[15]：

5 计算分析

5.1 水平井

若地层渗透率为0.05 D，地层厚度为10 m，生产压差为1 MPa，流体黏度为1 mPa·s，地层泄油半径为300 m，水平段长度为300 m，油井完井半径为0.1 m.把有关参数代入Renard-Dupuy公式得油井的产量为183.34m3/d，代入Joshi公式得油井的产量为178.74m3/d.

很显然，Joshi公式低估了油井的产量，但二者的差别并不大，仅为2.57%.

实际上，Joshi公式与Renard-Dupuy公式只是在分母上相差一个π，而且π又位于对数符号内，加上水平井的水平段长度远大于地层厚度，因此，不同等效方法对水平井的产量计算结果影响甚微。因此，尽管Joshi公式缺少理论上的合理性，但却一直保留了下来。