纯电动汽车传动系统扭转振动特性分析
2018-12-18刘成强徐海港柴本本陈林用
刘成强,徐海港,柴本本,陈林用
(1.山东时风(集团)有限责任公司,山东 聊城 252800;2.上海交通大学 机械与动力工程学院,上海 200240)
1 引言
纯电动汽车传动系统的扭转振动问题包含了驱动电机与机械传动系统的机电耦合,受到驱动电机磁场气隙变化和扭矩波动的影响。在车辆起步、加速时,驱动电机的扭矩波动直接传递到车辆,进而造成了车辆的起步喘振(surge),加速抖振(shuffle)现象[1-2]。文献[3]主要通过振动机械机电耦合的动态特性及研究,提出了多机耦合协同控制的理论。文献[4]对伺服驱动系统进行了机电耦合分析,讨论了机电参数对其的影响。文献[5]建立了电机集中式驱动车辆传动系统的仿真模型,分析了比较典型的传动系扭转阵型分布。一种部分集中式的传动系统建模方法在文献[6]中给出,并与分布式的建模方法作了比较。文献[7]讨论了功率分流式混合动力汽车传动系统的扭转振动对发动机启停的影响,分析了不同模式下变速器噪声的来源。目前的研究很少涉及对电驱动双速变速器传动系统的扭转振动研究,本研究以搭载双速变速器的某款纯电动乘用车为研究对象,运用Simulink建立包括动力传动系统模型和空间矢量控制的电机模型,并对二者的相互耦合进行了综合,系统研究了电驱动传动系统的机电耦合振动特性。
2 纯电动汽车传动系统概述
某款纯电动轿车的传动系统,驱动电机产生的驱动力先经过2AMT传入主减速器,再经由左右半轴传递到车轮上。车辆在起步加速或爬坡时,变速器采用一挡提供较大的扭矩来驱动车辆,提升车辆的牵引能力;在中高速时,采用二挡的直接挡使驱动电机尽可能工作在恒功率的高效区间,提升车辆的经济性。采用电驱动双速变速器动力总成可以在保证车辆最高车速和加速能力的前提下,降低驱动电机的额定功率,减少电机控制器和驱动电机的成本。
3 动力传动系的扭振建模
忽略齿轮的啮合间隙、传动系的摩擦损失,传动系统的扭转动力学模型可简化,如图1所示。
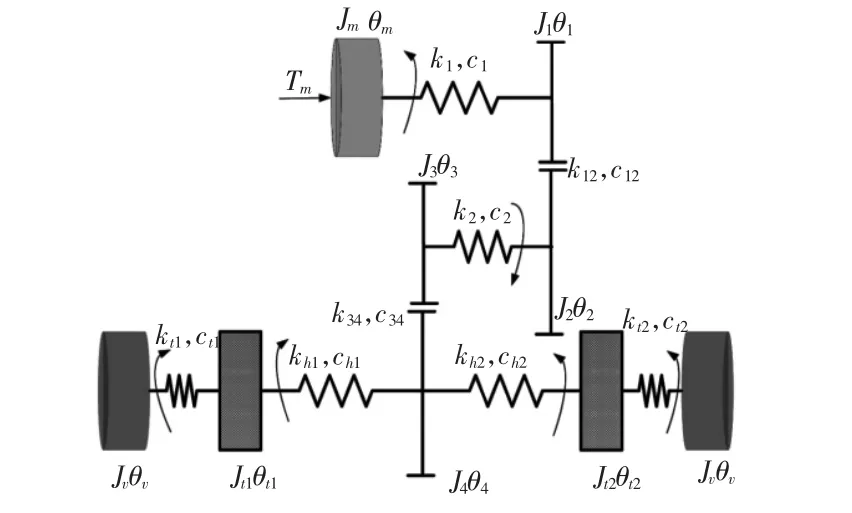
图1 某纯电动汽车传动系扭转动力学模型Fig.1 Torsional Vibrational Model of the Pure Electric Car Drivetrain
根据机械振动原理,选取各个部件的角位移作为变量,电机的电磁转矩经过电磁气隙作用到电机的转子端,从驱动电机端可以得到下动力学方程:

式中:Tm—驱动电机的输出扭矩;
k1和c1—分别变速器输入轴的扭转刚度和阻尼。
双速变速器为三轴式结构,输入轴的转矩经过Ⅰ/Ⅱ挡齿轮副到中间轴,然后通过主减速器传到输出轴,齿轮副之间通过齿轮的啮合作用来传递扭矩。进而得到变速器总成的扭转振动方程为:
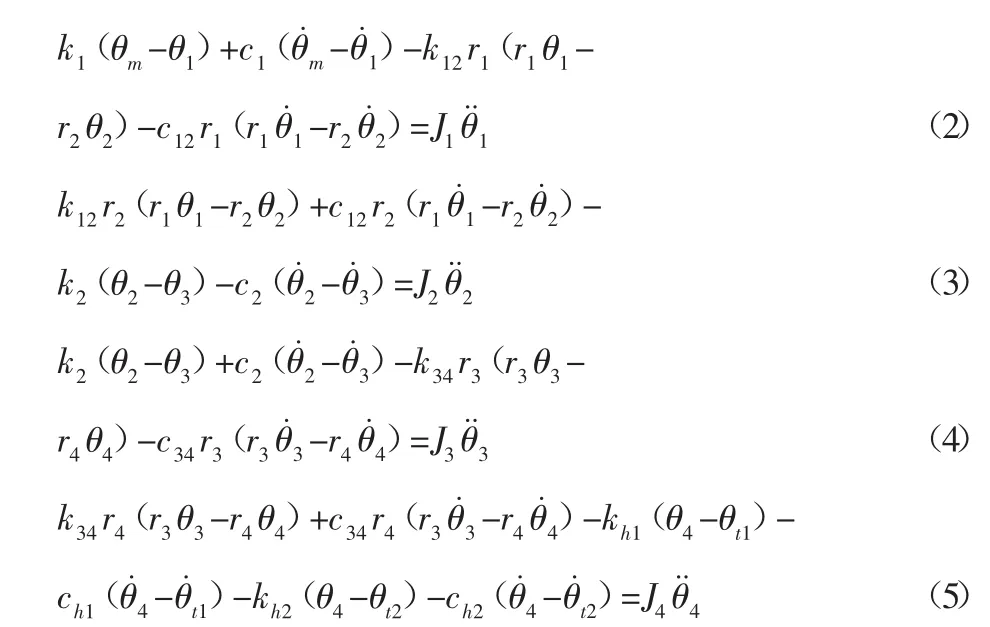
式中:k12和k34—Ⅰ/Ⅱ挡齿轮副和主减速器齿轮副的啮合刚度;c12和c34—Ⅰ/Ⅱ挡齿轮副和主减速器齿轮副的啮合阻尼;r1、r2、r3、r4—Ⅰ挡或Ⅱ挡齿轮副和主减速器齿轮副的基圆半径;k2和 c2—变速器中间轴的扭转刚度和阻尼;kh1、kh2、ch1、ch2—左右半轴的扭转刚度和阻尼。
不考虑车辆的转弯特性,差速器输出的扭矩经过半轴传递到车轮端,半轴可以看作具有刚度和阻尼的弹性元件,进而得到从半轴到车轮端的动力学方程为:
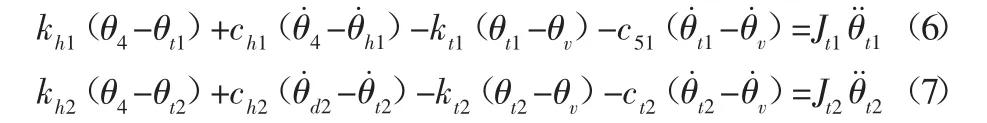
式中:kt1、kt2、ct1、ct2—轮胎的扭转刚度和阻尼。
轮胎与地面之间的接触作用,可以看作由于轮胎的弹性变形进而产生反作用力来驱动车辆,通过等效轮胎刚度的办法,建立从车轮到整车之间等效扭转动力学方程:
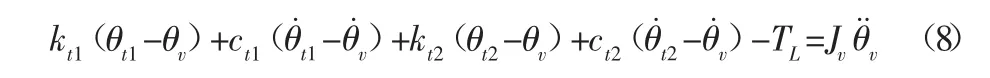
式中:TL—车辆行驶中受到的等效阻力矩,其表达为:

式中:f—滚动阻力系数;Cd—空气阻力系数;A—迎风面积;ρ—空
气密度;α—路面坡度;r—车轮半径;m—整车质量。
通过式(1)~式(9)联立,并忽略方程中的阻尼项及外加驱动力Tm,负载阻力矩TL,可以整合整个传动系无阻尼自由振动微分方程组:

式中:M—质量矩阵;K—刚度矩阵;X—广义位移向量。
其具体表达式为:

带入一挡和二挡时的质量和刚度参数,分别可以得到传动系的固有模态,如表1所示。

表1 传动系扭转振动固有频率Tab.1 Natural Frequencies of Drivetrain
将模态阵型归一化,并除去传动比的影响,得到一挡和二挡时整个传动系的各阶模态阵型,如图2所示。


图2 一/二挡时传动系的模态阵型图Fig.2 The Mode Shape of Driveline Natural Frequency at First or Second Gear
其中节点(1~7)依次为驱动电机、一挡/二挡主动齿轮、一挡/二挡被动齿轮、主减速器主动齿轮、主减速器被动齿轮、车轮和整车。一阶模态下,整车和车轮的振幅较大;二阶模态下车轮处的振幅较大;在高阶模态下,变速器内部齿轮的振幅比较明显。
4 永磁同步电机矢量控制仿真模型
该乘用车的驱动电机为同步电机,在中,其空间矢量控制模型主要包括电机本体、电压逆变器、速度和电流控制、SVPWM、电压坐标转换等模块。
其中,电机定子电阻R=3Ω,等效电感Ld=Lq=000085H,极对数np=4,转子磁链ψf=0.175Wb。其转速闭环过程中,永磁同步电机的转矩和转速响应,如图3所示。
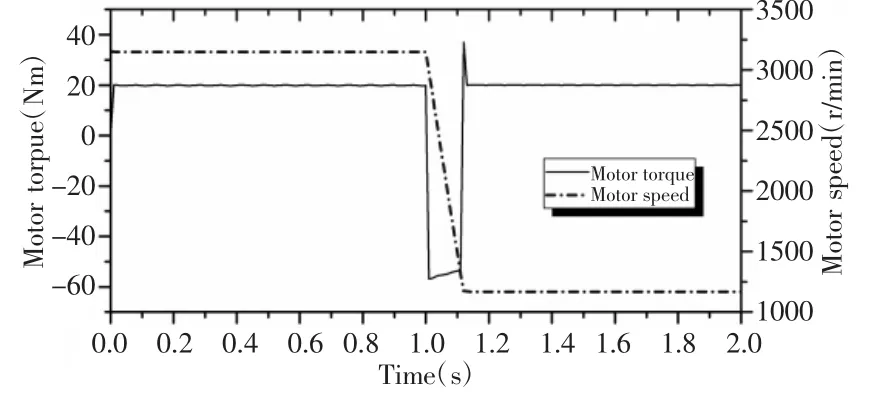
图3 永磁同步电机转速控制曲线Fig.3 The Speed Control Curve of Permanent Magnet Synchronous Motor
5 传动系机电耦合振动仿真
5.1 速度控制参数对系统机电耦合振动特性的影响
为研究速度控制参数Kp1和Ki1对驱动电机传动系扭转振动特性的影响,设 Kp1分别取 1,2,3;Ki1分别取 0.21,0.42,0.63 时整车角加速度时域响应,如图4所示。
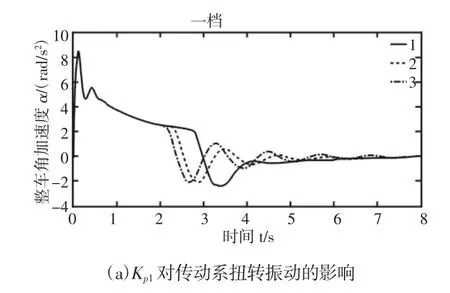

图4 速度控制参数对传动系扭转振动的影响Fig.4 The Influence of Velocity Control Parameters on Torsional Vibration of the Drivetrain
由图4可见,在Kp1逐渐变大时,(0~2)s车辆加速度呈现相同的变化规律。在(2~8)s时,整车加速度振幅由大变小,共振周期略提前。与Kp1作用相反,随着Ki1的增大,车辆加速度的振动响应延迟,振幅增大,波动时间更长。二挡和一挡的扭转振动响应类似,二挡传动比相对于一挡较小,整车加速度的幅值小于一挡,到达稳态的时间变长。
5.2 电流控制参数对系统机电耦合振动特性的影响
同样为研究电流控制参数Kp2和Ki2对电驱动传动系统扭转振动特性的影响,Kp2分别取 5,10,15;Ki2分别取 4,8,12 时,加速度时域响应,如图5所示。
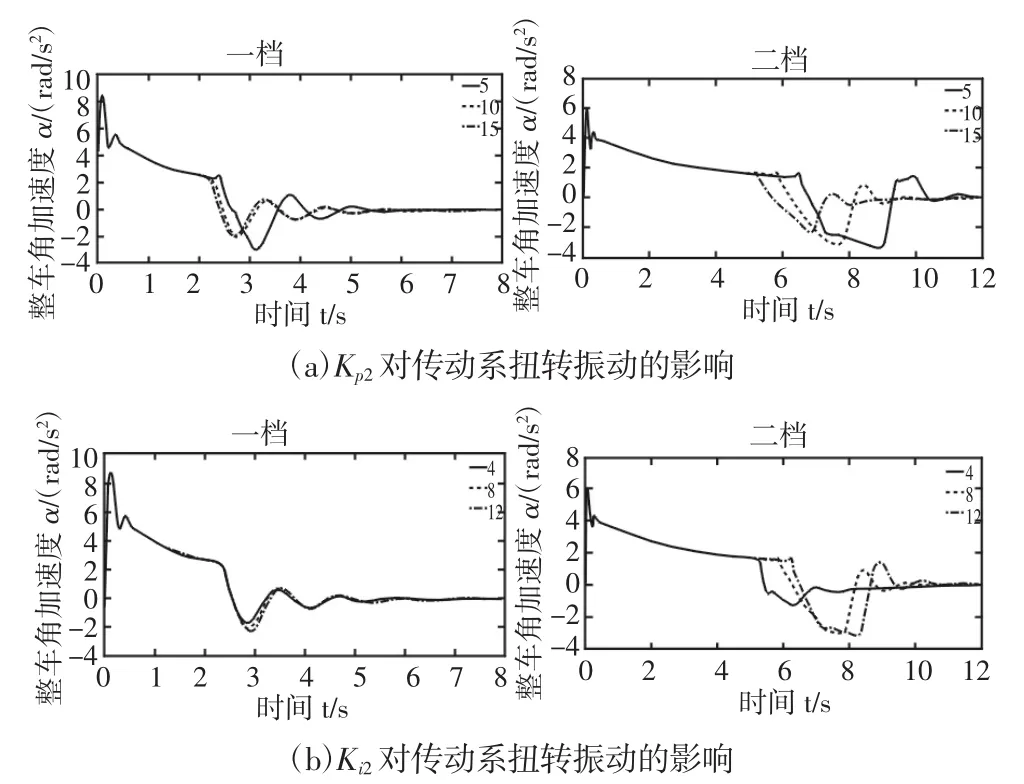
图5 电流控制参数对传动系扭转振动的影响Fig.5 The Influence of Current Control Parameters on Torsional Vibration of the Drivetrain
由图5可见,在(0~2)s时随着Kp2增加,车辆加速度的响应呈现相同的变化规律。在(2~8)s时,在Kp2=5附近时,车辆的角加速度振动的峰值和周期较长;在Kp2>10时,电流参数对车辆的角加速度影响不大。Kp2变化时二挡和一挡的振动呈现相同的变化规律。与Kp2相反,在一挡时,Ki2变化时,车辆的加速度变化不明显;在二挡时,随着Ki2增加,车辆的角加速度振动的峰值变大,而且振动周期显著增长。
5.3 轮胎刚度和阻尼对系统机电耦合振动特性的影响
轮胎刚度kt和阻尼系数ct的变化对传动系和整车振动亦有很大的影响。这里分别取 kt为 2250N·m·rad-1,4500N·m·rad-1和6750N·m·rad-1,取 ct为 53m·s·rad-1,106m·s·rad-1和 159m·s·rad-1计算整车加速度时域响应数值结果,如图6所示。由图6可见,随着轮胎刚度增加,在(0~1)s时车辆的加速度振幅增加,共振周期变长;在(2~8)s时,车辆的加速度振幅基本保持不变,但共振周期缩短。二挡与一挡呈现相同的变化规律。随着轮胎阻尼系数增加,在(0~1)s时车辆的加速度振幅减小,共振周期缩短,在(2~8)s时,车辆的加速度振幅和共振周期基本上不随阻尼系数变化。

图6 轮胎参数对传动系扭转振动的影响Fig.6 The Influence of Tire Parameters on Torsional Vibration of the Drivetrain
6 结论
通过建立2AMT动力传动系统的七自由度扭转振动动力学模型,分析了变速器不同挡位下的自由模态及其固有阵型;并运用Simulink把动力学模型转化为数值仿真模型。把永磁同步电机矢量控制模型与传动系扭转振动模型结合起来,分析了驱动电机速度控制参数、电流控制参数以及轮胎刚度和阻尼系数等因素对电驱动传动系统扭转振动的影响,为纯电动车动力传动系统的优化设计和车辆的扭转振动控制提供了参考,同时对永磁同步电机参数与纯电动汽车的匹配设计有重要价值。
