基于遗传算法的耦合隐马尔科夫模型的故障诊断方法
2018-12-18王绵斌李芬花
王绵斌,安 磊,李芬花,赵 钰
(1.冀北电力有限公司 经济技术研究院,北京 100038;2.华北电力大学 新能源电力系统国家重点实验室,北京 102206)
1 引言
研究机电设备的故障诊断方法,及时发现故障安排检修,有现实意义。而机电设备的故障信号中往往伴有较高不确定性和复杂关联性[1],因此需要研究出有效的识别方法以提高故障诊断精度。
隐马尔科夫模型(Hidden Markov Model,HMM)是一种时间序列信号统计分析模型,能够对振动信号这种非平稳、重复再现性不佳的时间序列信号进行有效分析。HMM最初主要用于语音识别[2],后被应用到机械设备的故障诊断[3]。耦合隐马尔科夫模型(Coupled Hidden Markov Model,CHMM)是一种HMM的改进模型,它是一种可描述两个或多个相互关联的随机过程特性的耦合模型[4]。设备的状态监测往往是多通道[5]同时进行的,而CHMM能够融合多通道数据的信息,进行更准确可靠的故障诊断[6]。
故障特征提取和状态识别是故障诊断研究中的关键[7],关系到故障诊断的可靠性和准确性。因此,我们尝试了从振动信号中提取多种特征[8]并改进状态识别方法[9]进行故障诊断,在对信号状态识别时,发现高灵敏度识别方法可对信号进行更多次状态识别,能提高故障诊断准确率且能在有效数据较少时进行准确诊断,且能够在有效数据不足的情况下完成有效诊断,对于设备的状态监测和故障诊断具有十分重要的意义。
基于以上分析,我们将CHMM用于故障诊断,综合考虑故障诊断的准确度和灵敏度,提出基于遗传算法的CHMM(GA-CHMM)故障诊断方法。通过对轴承位置不同的故障进行状态识别,验证了所提方法的可行性,且发现其能够在极少有效数据的情况下准确识别出故障的发生。
2 基础理论
2.1 隐马尔科夫模型
隐马尔科夫模型是,通过马尔科夫链(Markov Chain)描述基于概率的状态转移和观测值表现的双重概率模型。模型中的实际状态,实际中无法观测的隐含状态,只能通过观测值进行推测。HMM 具体描述,如式(1)~式(4)所示:
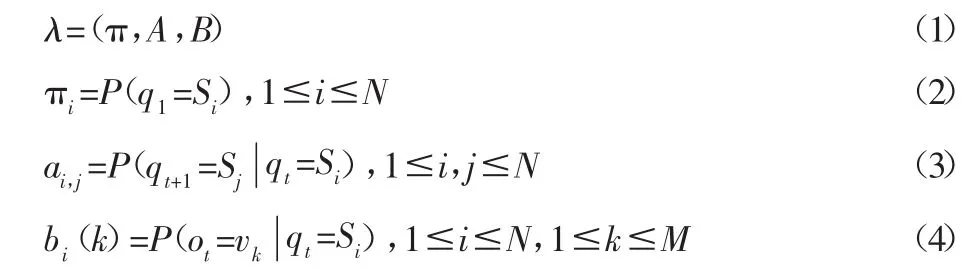
式中:π—初始状态概率向量,π={πi};A—状态转移概率矩阵,A={ai,j};B—观测值概率矩阵,B={bi(k)};N—模型的状态数,分别记作S1,S2,…,SN,模型时刻t所处的状态描述为qt,qt∈{S1,S2,…,SN};M—可能出现观测值数目,分别记作 v1,v2,…,vM,ot为 t时刻的观测值,ot∈{v1,v2,…,vM}。
2.2 耦合隐马尔科夫模型
耦合隐马尔科夫模型是由基于状态转移概率耦合的多个HMM 组成:对于含 n 条链的 CHMM,链 c(c=1,2,…,n-1,n)在t+1时刻的状态与t时刻同条链和耦合链的状态均相关,状态转移概率);但链c的观测值仅与同条链同时刻的状态相关,其观测值概率)。类似于HMM,CHMM的具体描述,如式(5)~式(8)所示:
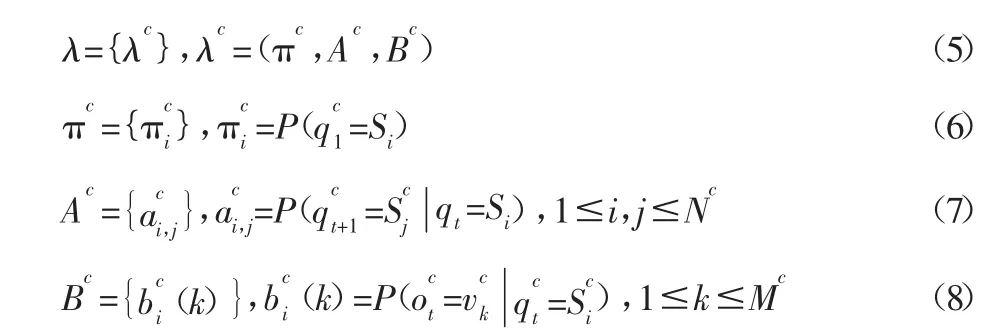
式中:πc—链c的初始状态概率向量;Ac—链c的状态转移概率矩阵;Bc—链c的观测值概率矩阵;Nc—链c的隐含状态数,分别记作,模型在时刻t所处的状态描述为∈{—链c可能观测值数目,分别记作v1,v2,…—t时刻的观测值∈{v1,v2,…,vM}c。
为降低原始信号的失真程度,CHMM中的隐含状态的观测值概率由高斯混合模型(GMM)确定,将原本离散的观测值变为连续的观测值,可不进行聚类而直接使用经去噪处理的信号作观测值,保证信号信息的完整性。
2.3 遗传算法
遗传算法(Genetic Algorithm,GA)是一种借鉴生物自然选择和遗传机制的随机搜索算法,它能较为准确的找到全局最优的目标。
其具体方法为[10]:(1)参数初始化:确定种群规模、交叉概率、变异概率;(2)评价运算:计算群体中个体的适应度;(3)选择运算:根据选择算子从群体选择母本,其基本原理为群体中的个体适应度值越大被选择的概率就越大;(4)交叉运算:用交叉算子使母本进行基因编码交叉生成中间个体,使优秀基因编码交叉组合生成更好的个体;(5)变异运算:用变异算子使中间个体基因编码变异,以生成带有未出现或已失去的基因编码的子代,这能降低陷入局部最优的可能;(6)终止条件判断:重复选择-交叉-变异,直到达到最大进化代数,最后将进化过程中所得到适应度最大的个体作为最优解输出。
3 基于GA-CHMM的状态识别方法
GA-CHMM是通过遗传算法优化参数使CHMM识别更加准确灵敏的识别方法。其具体步骤如下:
3.1 N和L优化选取
隐含状态数N和每组观测值向量包含的数据量L为这里CHMM需要确定的参数,为找到能够使CHMM准确灵敏的参数N和L,我们采用的参数优化算法为遗传算法,具体优化过程,如图1所示。

图1 CHMM参数优化流程图Fig.1 Parameter Optimization of CHMM
编码方法选为格雷码编码,假设二进制码X=xm…x2x1,其对应的格雷码Y=ym…y2y1,则:
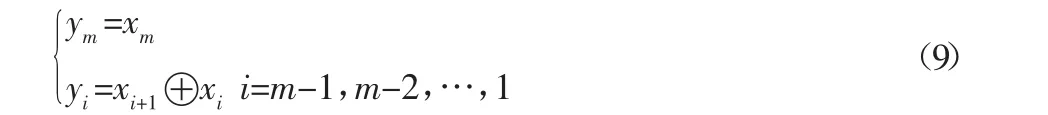
目标函数设定为N与L的函数,即按照生成的N和L计算CHMM 识别准确率 acc(N,L),再以准确率 acc(N,L)和 L 计算出适应度,即:

式中:α—适应度中识别准确率的比重,α反映识别准确性的重要程度,(1-α)则反映识别灵敏度的重要程度;Lmax—L取值范围中的最大值。
为减小计算量,我们加入了简化适应度计算的步骤:预设全局变量以保存计算出的准确率,不再重复运算。
3.2 模型训练
将观测值数据划分为每组数据量为L的观测值向量,之后按照Baum-Welch算法,利用观测值向量更新CHMM各链参数。
3.3 状态识别
根据Viterbi算法,计算待识别观测值o在各状态模型下的似然概率最大的状态即为该观测值向量o所处的状态。具体故障诊断流程,如图2所示。即:(1)对带有状态标签的历史数据进行预处理,剔除无效数据,并根据信号采集点数量确定CHMM的耦合链数量;(2)采用遗传算法优化CHMM的初始参数,以预处理后的数据训练CHMM,建立各状态下的模型参数;(3)对实际、未知状态的数据进行预处理,再用各状态的模型参数计算似然概率,判别实际状态。其中状态可设置为发生故障概率,或故障发生的不同位置、程度。

图2 基于GA-CHMM的故障诊断流程图Fig.2 Fault Diagnosis Based on GA-CHMM
4 实验分析
为证实基于此种参数选择方法的CHMM状态识别效果,我们根据凯斯西储大学的滚动轴承实验数据进行CHMM故障诊断实验验证。实验设备,如图3所示。实验中采用轴承型号为6205-2RS JEMSKF的深沟球轴承,加速度传感器位于驱动侧与被驱动侧电机顶部,采样频率为12kHz,测试故障位置位于驱动侧轴承,共5种,分别为内圈、滚动体以及外圈的底部、中部和顶部,测试损伤为直径0.007英寸(0.1778mm)的单点故障。我们将驱动侧与被驱动侧两处采集的数据作为CHMM两条链的数据,取采样时长为0.5s的数据作训练数据,采样时间为5s的数据作测试数据。

图3 实验设备Fig.3 Experimental Equipment
其中,用于训练和测试CHMM的数据都是未进行特征提取的振动加速度数据,因为CHMM能有效地对振动变化特性进行表现,且能够得到比分帧特征提取灵敏度更高的系统。所以,本识别系统在CHMM的训练速度稍差于特征提取后的CHMM,但省去了特征提取的时间。初始范围设定为 N∈[2,10],L∈[10,300],参数α取值为0.99,根据遗传算法用训练数据对隐含状态数N和每组包含的数据量L进行参数寻优,结果为隐含状态数N=7,每组数据量L=90。具体适应度变化,如图4所示。在遗传算法参数优化过程中会出现大量的重复计算,本实验中非重复运算共167次,即本方法实际计算适应度次数为167次,而遍历寻优需要进行(10-2)×(300-10)=2320次运算,遍历寻优计算量是本寻优方法的13.89倍,该寻优方法能有效减少运算。

图4 遗传算法适应度曲线Fig.4 Curve of Fitness
为验证结论的正确性并探究观测值向量中L和N对CHMM识别效果的影响规律,这里取 N∈[2,10],L∈[10,300],进行CHMM识别测试结果,如图5所示。
当L较低且N小于7时,随着N增大,如图5所示。故障状态识别准确率增高,N大于7时,随着N增大,识别准确率降低;随着L增加,识别准确率的最高点逐渐向N减小的方向移动;N∈[3,8],随着每组内的数据量L增加,识别准确率稳定在90%上,之后准确率增长减缓,但当N取值为2时,准确率会出现波动剧烈。其中,隐含状态数目N和每组数据量L分别为7与90时,识别准确率为94.84%,这说明遗传算法参数优化的结果虽然不是最高准确率,但确实兼顾了准确率和灵敏度。

图5 六种状态在不同N与L下CHMM测试结果Fig.5 CHMM Test Results of 6 States in Different N and L
为验证该方法的灵敏度,我们将90组正常状态数据与90组各个状态数据进行拼接,测试其识别效果。图6中,识别状态的“1,2,3,4,5,6”分别表示“正常状态、滚动体故障状态、内圈故障状态、外圈底部、中部和顶部故障状态”;正常状态与正常状态、滚动体故障状态、内圈故障状态、外圈底部、中部和顶部故障状态拼接的振动数据(只保留故障种状态的振动数据)和识别结果,如图6所示。

图6 状态转变数据识别结果图Fig.6 Recognition Results of States Transition Data
最多需要80组故障数据就能准确识别状态,即采集80÷12000=0.0067s的有效振动数据能够进行有效故障诊断。测试结果证明了此种N的参数范围估计方法有一定的参考意义,且基于遗传算法参数优化的CHMM能够准确、灵敏地识别故障发生位置。
5 结论
为提高故障诊断效率,提出了一种基于遗传算法参数优化的CHMM的故障诊断方法,并测试了正常状态与5种模拟故障状态下轴承的故障诊断效果。结果表明:(1)CHMM能利用原始振动数据进行建模,并保持较好的识别效果,可省略特征提取步骤用CHMM进行更灵敏的诊断;(2)遗传算法能对CHMM的参数进行有效优化,且该优化算法运算量相对较低;(3)基于GA-CHMM的故障诊断方法能够准确、灵敏的进行状态识别,快速识别出故障发生。
