不同端部形状的编织型食管支架应力及疲劳性能的研究
2018-12-18倪晓宇张嫣红眭蓓蓓潘长网
倪晓宇,张嫣红,眭蓓蓓,潘长网
(1.南京林业大学 机械电子工程学院,江苏 南京 210037;2.南京微创医学科技股份有限公司,江苏 南京 210069)
1 引言
因编织型支架同时具有柔韧性和足够的支撑强度[1],而在食管等非血管领域应用广泛。编织型支架的设计包括结构参数设计和端部形状设计,确保支架中部具有一定的径向刚度撑开狭窄区域和在蠕动波和食物吞咽的情况下支架不发生移位。目前较为常见的端部形状有直筒形、杯球形和双喇叭形等。
植入食管后的支架会因食管蠕动波发生疲劳断裂而引发严重的并发症,因此疲劳性能是编织型支架的一个重要力学性能指标。影响支架疲劳性能的主要因素是结构参数[2-3],但置于食管健康区域的支架端部也会因承受较大的弯扭组合变形而产生较大的应力或应力集中,因而会对支架应力分布特征以及支架整体疲劳性能产生较大影响,但目前未见相关报道。此外,国内外对支架疲劳性能的分析测试基本集中在激光雕刻的血管支架[4-7],而在编织型自膨胀支架的疲劳性能等方面的研究相对较少。评价支架疲劳性能的常用方法是Goodman准则[8]。美国FDA推荐用Goodman准则、限元分析和加速疲劳测试对支架作疲劳寿命评价,以确保安全性和有效性[9]。鉴于此,通过模拟支架在食管内的工作状态,分析支架端部形状对支架整体应力和疲劳性能的影响,以Goodman准则来完成不同端部形状的编织型食管支架疲劳性能的评价,为支架端部形状设计提供理论依据。
2 材料与方法
2.1 支架-食管的有限元模型
以编织型双螺旋支架为例,如图1(a)所示。根据结构参数对疲劳性能影响的研究结论[2],选择具有最佳疲劳特性的支架结构参数,如表1所示。建立三种不同端部形状的支架几何模型。因丝线截面尺寸远小于丝线长度,丝线在支架受载时会产生弯扭变形,故选用梁单元Beam188来完成支架有限元模型的创建,如图1(b)所示。

表1 不同端部形状支架的结构参数Tab.1 The Structural Parameters of Braided Stents with Different End Shapes

图1 支架产品照片及有限元模型(从上到下:直筒形、杯球形、双喇叭形)Fig.1 Bracket Product Photo and Finite Element Model(From Top to Bottom:Straight-Shaped;Cup-Spherical-Shaped;Double-Trumpet-Shaped)
依据食管解剖学中成年人食管的尺寸范围取其平均值,并假设食管肿瘤为环向内生长,如图2(a)所示。设定h=4mm,l=45mm,建立病变食管的几何模型。食管与肿瘤组织均采用Solid185单元模拟,初始状态下支架-食管耦合系统的有限元模型,如图 2(b)所示。

图2 肿瘤示意图及支架-食管耦合系统有限有模型(从上到下:直筒形、杯球形、双喇叭形)Fig.2 The Tumor Diagram and the Stent-Esophageal Coupling System have Limited Models(From Top to Bottom:Straight-shaped;Cupspherical-shaped;Double-trumpet-shaped )
2.2 材料属性
支架材料为镍钛合金。体温下,处于奥氏体状态的镍钛合金丝具有超弹性。此外,编织型支架结构也具有弹簧性质,在其工作状态下,丝线截面不会发生很大的变形,丝线长度也不会有较大的变化,故采用线弹性本构关系来描述支架丝线的材料特性[11],如表2所示。
目前,食管材料和肿瘤组织两者的材料参数都无参数可查,但两者都具有黏弹性和不可压缩性[10],且临床上与血管较为相似,因此将其设定为与血管组织较为接近的线弹性材料来进行模拟,即肿瘤组织的弹性模量E=2.19MPa,泊松比μ=0.499,食管的弹性模量E=1.75MPa,泊松比μ=0.499[11]。

表2 镍钛合金的材料属性Tab.2 Material Properties of Nitinol
2.3 边界条件
(1)自由度约束。选择柱坐标系建模,Z轴为支架的轴线方向,X轴为支架的径向方向。选择支架中部一层节点固定其Z方向的自由度,确保支架Z方向上无刚体位移,但支架在Z方向上能自由伸缩;选择支架XZ平面和YZ平面上的节点固定其Y方向的自由度,确保支架无周向刚体位移,但径向方向可自由压缩与扩张。食管模型的约束设置与支架完全一致。
(2)载荷条件。食管和病变组织对支架的径向压缩和食管蠕动波对支架结构的径向压力。食管和肿瘤组织对支架的径向压缩由支架-食管耦合系统间力的平衡自行完成。根据蠕动波的特点(单向正波、波形对称)以及食管中部蠕动波参数[12](速度v=30mm/s,峰压值Pp=9.8kPa,时程t=3s)以及支架长度,将蠕动波看成多个峰值压力为9.8kPa的交变径向压力。
2.4 求解设置
(1)接触设置。计算模型存在2种接触,即支架交叉丝线间的接触和食管内壁与支架的接触。通过对实际支架的观察发现,支架受载时,交叉丝线在其接触点处有相对转动但无相对滑动。为提高非线性求解的收敛性,采用自由度耦合来模拟交叉点间的运动关系。支架与食管壁之间的接触设置为“点-面”接触形式,算法设定为罚函数法。
(2)载荷步设置。第一载荷步将支架压缩至狭窄的食管内;第二载荷步,释放载荷、支架自扩张至食管-支架耦合系统间的力平衡;第三载荷步在食管外壁与支架两侧和中部对应的三个位置上施加蠕动波载荷。此外,在第一载荷步中,将不参与计算的接触单元和食管模型单元“杀死”;在第二和第三载荷步中,所有单元都将参于计算,被“杀死”的单元全部激活。
3 计算结果
3.1 支架应力分析
第二载荷步计算结束后可获得食管-支架耦合系统力平衡状态,如图3所示。在此基础上,完成第三载荷步计算。结果显示,支架中部和端部都会出现较大应力,最大应力值,如表3所示。直筒形支架的最大应力出现在支架中部,端部应力偏小;杯球形支架的最大应力出现在杯形端部,支架中部的应力也比较大,在蠕动波0kPa和9.8kPa作用下,分别为641.868MPa和694.753MPa;双喇叭形支架的最大应力出现在支架中部,但端部应力与中部应力较为接近,分别为633.744MPa和691.664MPa。很明显,杯球形支架的杯形端部及其中部的最大应力值均比直筒形和双喇叭形支架同样位置上的最大应力值大。
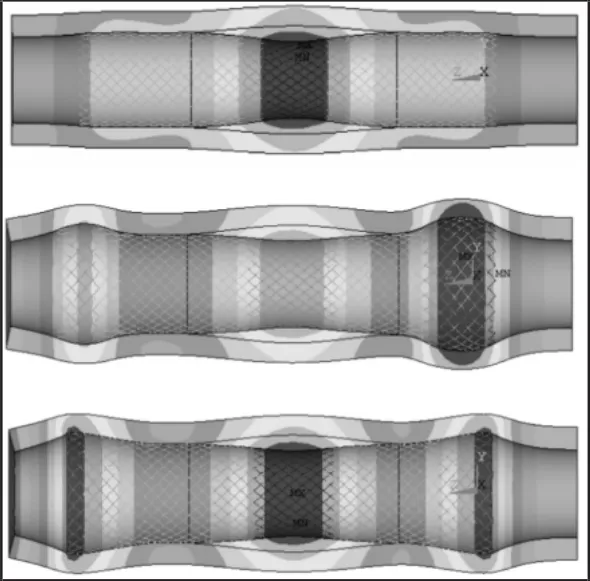
图3 支架-食管耦合系统的平衡状态(径向变形,从上到下:直筒形、杯球形和双喇叭形)Fig.3 The Stent-Esophagus Coupling System in the Equilibrium State(Radium Deformation,From Top to Bottom:Straight-Shaped;Cup-Spherical-Shaped;Double-Trumpet-Shaped)

表3 支架工作状态下的最大应力tTab.3 The Maximum Stress Under Working Condition of Stents
3.2 疲劳分析
工程中将疲劳极限σ-1与抗拉强度σb之比称为疲劳比k:

镍钛合金疲劳比一般在(0.3~0.6)之间[13],拉伸强度为1564MPa,选择最小的疲劳比k=0.3,则镍钛丝的疲劳极限为:

式中:σa—交变应力,由纵坐标表示;σm—平均应力,由横坐标表示;
记录支架所有节点在蠕动波持续作用下的循环应力的平均应力和应力幅值,并根据式(3)绘制出Goodman曲线,如图4所示。若支架每个点在0kPa和9.8kPa下的应力平均值和应力差值都位于曲线下方,则支架在其工作状态下安全。
基于Goodman的支架疲劳性能图,看出不同端部形状的支架在其工作状态下各点应力均在安全区域内,从理论上说明蠕动波载荷引起的交变应力不会造成支架的疲劳断裂。比较图4(a),图4(b)和图4(c),能明显看出,直筒形支架各点的应力离Goodman疲劳极限曲线最远,双喇叭形支架次之,杯球形支架则有多个点与疲劳极限接近,即直筒形支架的疲劳性能最佳,而杯球形支架的疲劳性能相对较弱。这是因为直筒形支架在其工作状态下的不会产生应力集中,应力相对平缓,而杯球形支架的杯形端部因其外径较大而产生较大的变形和应力;此外,支架本体与杯形端和球形端的连接区域会在支架径向压缩时因丝线发生扭曲而造成较大的应力,故杯球形支架的疲劳性能相对较弱。
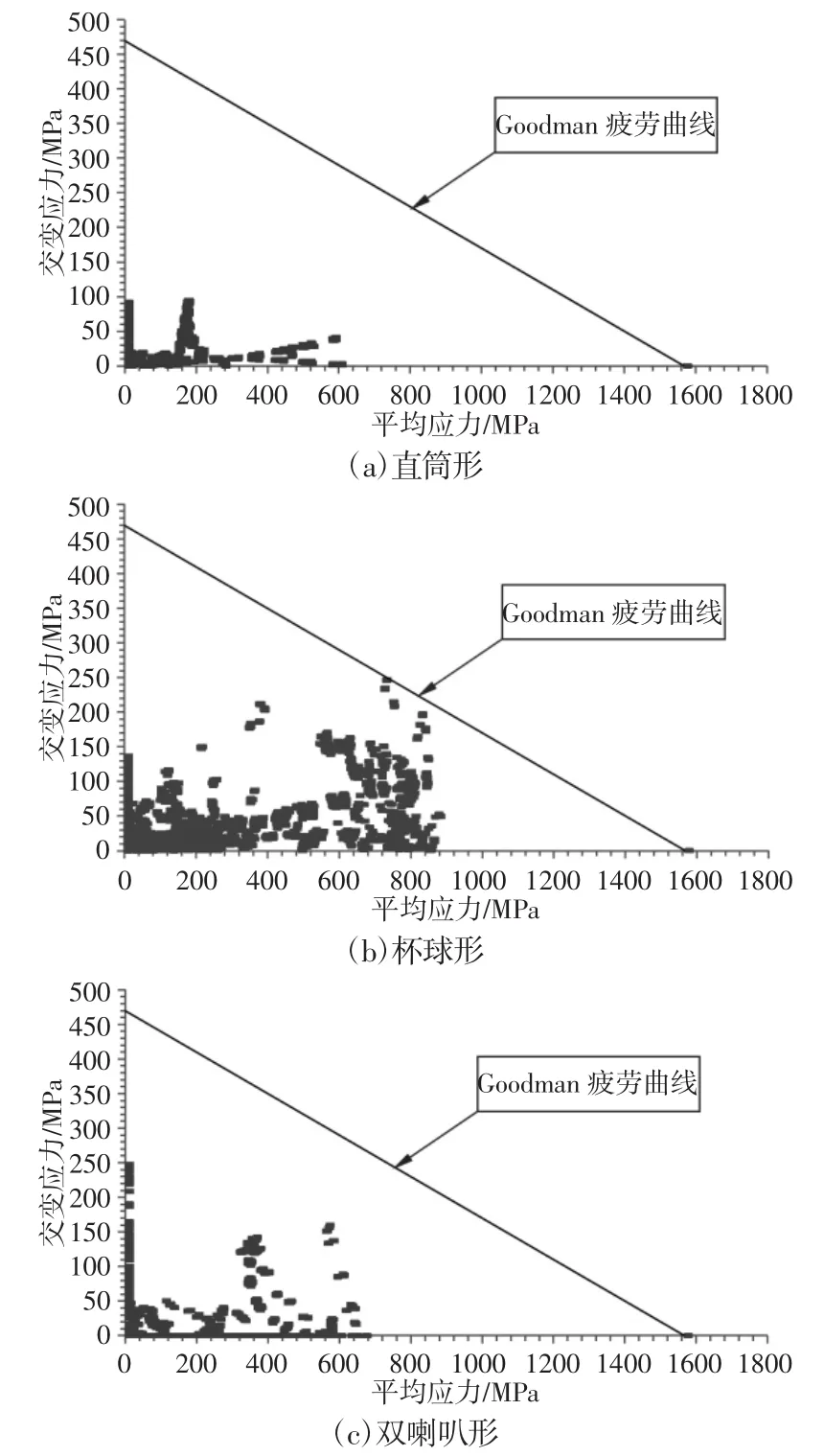
图4 支架疲劳性能的Goodman图Fig.4 The Fatigue Performance of the StentsBased on Goodman
4 结论
支架在工作状态下的应力分布情况会根据支架端部形状而发生变化,杯球形支架在其端部和中部的应力均大于直筒形和双喇叭形支架。端部形状对支架疲劳性能也存在一定的影响,根据Goodman图,三种不同端部形状的支架都满足疲劳强度的要求,但在相同条件下,直筒形支架的疲劳性能最好,而杯球形支架发生疲劳断裂的可能性最大。在研究食管支架应力分布和疲劳性能过程中存在两个局限性,一是在研究支架-食管耦合系统时,因为食管材料属性参数的近似性可能会引起一定的误差;二是食管及其病变组织模型的理想化,未考虑食管病变组织的个体差异对食管支架的疲劳性能的影响。
