轴承振动信号的去趋势分析和故障特征提取方法研究

2018-12-18田锐

机械设计与制造 2018年12期

田锐

（荆楚理工学院，湖北荆门 448000）

1 引言

在流程工业中大多数设备都处在高速、重载和强磁场的环境中，滚动轴承作为重要的零部件，其发生故障会导致机械设备停机，因而对滚动轴承的故障状态进行智能诊断有实用的价值。轴承故障信号具有非线性、非平稳的特性，传统频谱分析方法主要针对周期平稳信号，因此这些方法不能完全提取信号所含有的信息，具有一定程度的局限性。一些非平稳信号的处理方法如：时频分析[1]、小波变换[2]及小波变换的变种[3]、多分辨奇异值分解[4]等方法虽然改进了传统方法的不足，但是针对早期微弱故障信号，其也很难取得理想的效果，主要是由于这些方法本身在理论上也存在一些局限性。

经验模式分解（Empirical Mode Decomposition，EMD）[5]具有正交性、完备性和自适应性的特点，在信号处理和故障诊断方面得到了相关运用[6-7]，但是其存在模态混叠和端点效应等问题限制了其进一步地推广。集合经验模式分解（Ensemble Empirical Mode Decomposition，EEMD）[8]重要特点是通过添加白噪声辅助信号来部分地减弱模态混叠现象。但是，加入正、负对辅助噪声的方法，能够更大程度地消除重构信号中残余的辅助噪声，并且提高计算效率，因此互补集合经验模式分解（Complementary Ensemble Empirical Mode Decomposition，CEEMD）[9]被引入到信号分解中。去趋势波动分析（Detrended Fluctuation Analysis，DFA）是由文献[10]提出的一种计算标度指数的方法，能够将信号的各阶外来趋势项从时间序列中去掉，进而精准地得到时间序列所具有的统计行为特性。文献[11]将其引入到基于EMD的降噪方法中，首先通过标度指数来确定与噪声相关的IMF分量，然后通过舍弃与噪声相关的IMF分量来重构信号，该方法相比传统基于经验假设的模式分解方法有了较大的进步，但是该方法也存在着以下不足：直接舍弃与噪声信号关联的IMF高频分量会丢掉高频信号中所包含的有用信息，因为工业现场采集到的信号往往具有非线性、非平稳、非高斯的特征，其经过EMD、EEMD获得的模式分量依然存在模态混叠的现象，因此噪声信号和高频有用信号同时存在于高频模式分量中，如果直接舍弃高频分量也许会导致故障的高频及其倍频成分无法有效提取。

基于CEEMD分解和去趋势波动分析，提出了一种针对含噪高频模式分量的定量判别方法。首先利用DFA对CEEMD分解得到模式分量IMFs计算标度指数，并以此为依据判别是否为含噪分量，然后对含噪模式分量进行小波降噪。这样做不仅为正确选取含噪模式分量提供了评价指标，同时最大程度地保留了高频模式分量中含有的高频有用信息，便于故障特征提取。

2 基本原理

2.1 EMD与CEEMD的基本原理

EMD主要根据信号的包络特征进行自适应分解，其基本的计算步骤如下：

（1）对待处理信号x（t）进行分析，确定局部极值点；

（2）利用三次样条插值法分别拟合极大值、极小值，从而获得x（t）的上包络线和下包络线；

（3）从 x（t）中减去其上、下包络线的均值 m（t），得到：

判断h1（t）是否与固有模态函数的定义相吻合，若不吻合需要重复上述步骤，进而求出h1（t）的包络平均值m11（t），并且计算h1（t）与 m11（t）的残差：

重复上述步骤k次，直到h1k（t）满足IMF的条件。频率分量最高的即为第一个固有模态函数，记为 c1（t）=h1k（t）。

（4）从 x（t）中减去 c1（t）得到剩余值序列 r1（t），即：

（5）残差r1（t）作为新的待处理信号重复以上步骤，迭代的终止条件为分解不出IMF分量或者最后一项为单调函数。因此，原始信号x（t）可以表示成如下形式：

式中：c2（t），c3（t），cn（t）—第二、第三及第 n 个固有模态函数；rn（t）—余项。

尽管EMD分解具有自适应的优点，但其存在模态混叠等诸多问题，因此其对复杂信号的分解能力很弱。CEEMD分解是以EMD分解为基础的，其主要特点是能够提高计算效率，减少冗余模式分量的产生和模态混叠的现象。主要包括以下三个步骤：

（1）以正、负对的形式将n组辅助白噪声添加到原信号中，获得的集合记为：

式中：x（t）—原信号；w（t）—辅助噪声；M1、M2—添加的正、负对噪声后的信号，集合中信号个数为2n。

（2）将上述集合中的全部信号采用EMD方法进行分解，每个信号分解后由一组IMF分量组成，将第i个信号的第j个IMF分量记为cij。

（3）通过多组分量组合的方法获得分解量：

式中：cj—CEEMD最终分解得到的第j个IMF分量。

2.2 去趋势波动分析的原理

对一维时间序列 x（t），t=1，2，3，…，N，其去趋势波动分析的计算步骤如下：

（1）求时间序列 x（t），t=1，2，3，…，N，的累积离差：

（2）将累积离差y（k）等分为Ns个不重叠的窗口，其中每个窗口含s个采样点，从而Ns=［N/s］。每一个区间都可以表示成一个与时间t相关的p阶趋势，则其对应的趋势方程可表达为如下形式：

式中：系数βj（j=0，1，2，…，p）利用最小二乘拟合法获得。

（3）消除每一窗口时间序列y（k）的趋势项ys（k）：

（4）时间序列Δys（k）的二阶波动函数利用下式计算出：

（5）窗口大小 s按照一定步长递增，重复（2）～（4）步，可得到函数F（s）随窗口大小s变化的曲线。若该曲线服从幂律关系，则存在：

由上式可以发现lg（F（s））与lg s表现为线性相关，其标度指数α即斜率，可以采用最小二乘法获得：

2.3 提出方法的步骤

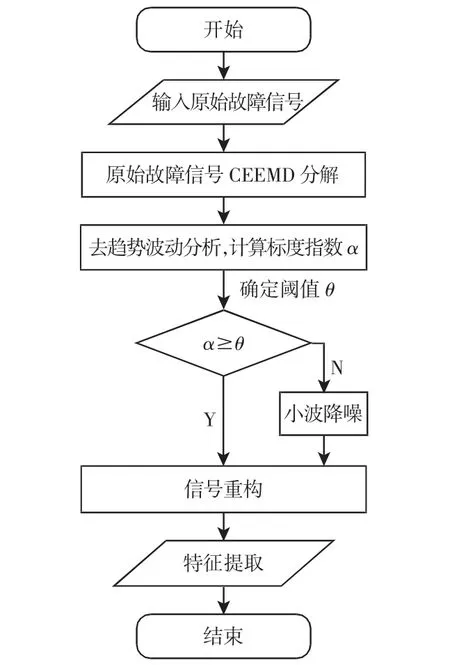
图1 提出方法的流程图Fig.1 The Flowchart of Proposed Method

对于机械设备故障信号，提出方法的主要思路是通过CEEMD方法将原始故障信号进行模式分解，采用DFA方法对与噪声相关联的模式分量进行表征，其流程图，如图1所示。

提出方法的具体实现步骤如下：

（1）采用CEEMD分解得到故障信号x（t）的模式分量IMFi（i=1，…，n）；

（2）利用去趋势波动分析计算IMFi（i=1，…，n）对应的标度指数αi（i=1，…，n）；

（3）确定标度指数阈值θ，标度指数小于阈值θ对应着与噪声相关联的模式分量IMFp（p=1，…，t，t≤n），标度指数大于阈值θ对应着与噪声无关的模式分量IMFq（q=1，…，e，e≤n，n=e+t）；

（4）采用小波降噪对含噪分量IMFp进行下一步的降噪处理；

（5）将降噪后的IMFp和IMFq一起重构，并进行故障特征分析。

3 仿真信号及结果分析

当滚动轴承发生故障时，其振动信号包含着很多故障信息，振动信号一般都含有谐波成分、调制成分以及噪声成分。因此，用到的数值仿真信号由以下部分组成：

式中：x3—均值为 0、方差为 0.8 的高斯白噪声，f0=50Hz，f1=50Hz，f2=40Hz，1≤t≤1000。

正弦信号x1，调制信号x2，复合信号的时域波形，如图2所示。采用CEEMD对原始信号进行分解计算，如图3所示。得到9个模式分量IMFi（i=1，…，9）。然后对分解后得到的IMFi分别计算其标度指数，标度指数的阈值设定为θ=0.5，通过图4可以发现前面5个模式分量IMF1的标度指数在阈值0.5以下，因此可以确定这些模式分量包含噪声信号。分解后模式分量标度指数分布图，如图4所示。

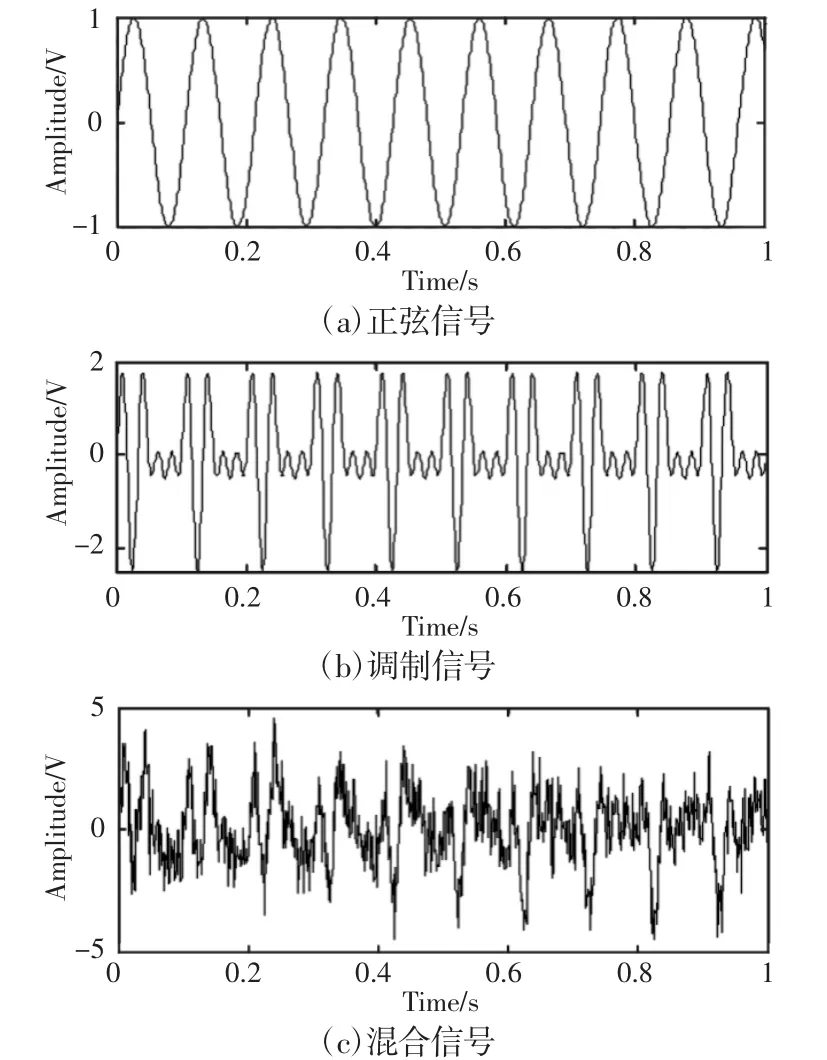
图2 不同信号时波形Fig.2 Different Signals When Waveform

图3 合成信号经过CEEMD分解后的模式分量Fig.3 The Mode Decomposition of Composite Signal by CEEMD

图4 分解后模式分量标度指数分布图Fig.4 The Scaling Exponent of Each Decomposed Mode Component

为了进一步比较提出的方法与Mert提出的EMD-DFA方法，以及传统的模式分解降噪方法的不同，对于上述仿真信号分别进行了对比分析。Mert提出的EMD-DFA方法在利用DFA对EMD分解的模式分量进行标度指数分析后，直接将与噪声相关联的模式分量去掉，然后再进行信号的重构。传统的基于模式分解降噪方法，主要是通过分解后的模式分量与原始信号互相关系数最大的原则来选取重构的模式分量，从而实现降噪。由图3可知，第4个模式分量对应的相关系数最大，将其进行信号的重构。上述三种方法的对仿真信号的降噪效果，如图5所示。利用均方根误差（Root Mean Square Error，RMSE）来定量地评价实际信号降噪的效果，提出的方法、EMD-DFA的方法、传统模式分解降噪的方法的均方根误差，如表1所示。由表1可以可知提出的方法更适合于振动信号的降噪。

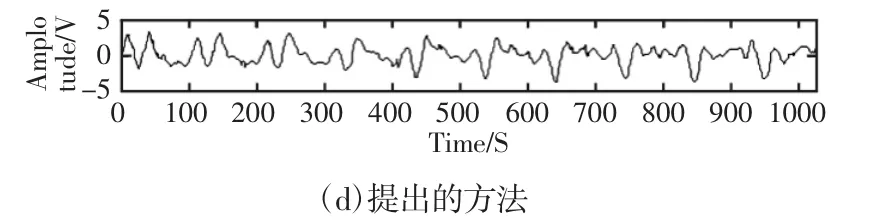
图5 三种不同降噪方法的结果比较Fig.5 The Comparison of Different Method in Denoising Performance

表1 不同降噪方法的均方根误差Tab.1 The RMSE of Different Denoising Method

4 实测信号分析及结果

采用滚动轴承故障实验台的数据来验证所提出的方法对实测轴承故障信号的特征提取和分析的可靠性。实验台的实物图，如图6所示。整个实验装置由一台550W（220V～50Hz）交流电机带动，图6中指引线3所示位置为可更换轴承，轴承的故障信号为垂直方向上的加速度振动信号，此故障采用电火花工艺对轴承的外圈进行点蚀加工获得，并且利用美国CSI2130数据分析仪采集，用到的轴承型号为深沟球轴承6207（内径d=35mm，外径D=72mm，滚动体数目为9），加速度传感器为PCB-352C33。采用实验台的各个工作参数和故障频率，如表2所示。

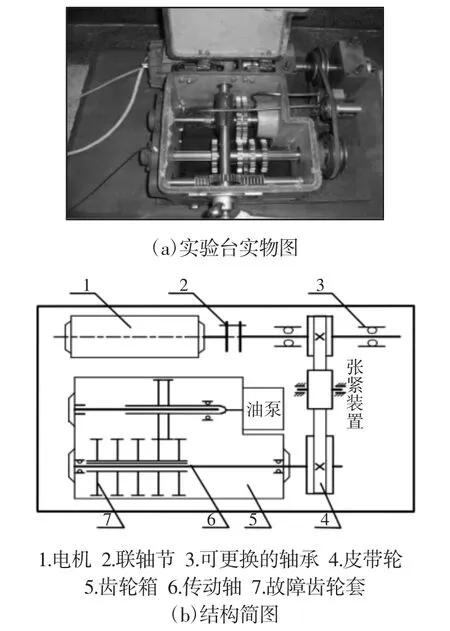
图6 轴承故障模拟实验台Fig.6 The Rolling Bearing Experiment System

表2 实验参数及故障频率Tab.2 The Equipment Operating Parameter and Fault Frequencies

实际测得的轴承故障信号的时域和频域图，如图7所示。从图7中可以发现轴承的故障信号存在明显的冲击成分，并且从频域波形中很难识别转频、及其对应的倍频成分，轴承内圈故障的一倍频（87Hz）和二倍频（174Hz）不易被识别，容易被其他成分掩盖，因此没有被这里方法进行特征处理前效果并不明显。

首先对此实测故障信号进行CEEMD模式分解处理，获得14个模式分量IMFi（i=1，…，14），然后计算每一个分解的模式分量的标度指数，此时仍然选择标度指数的阈值为0.5，作为判断模式分量是否含噪声的标准，如图8所示。

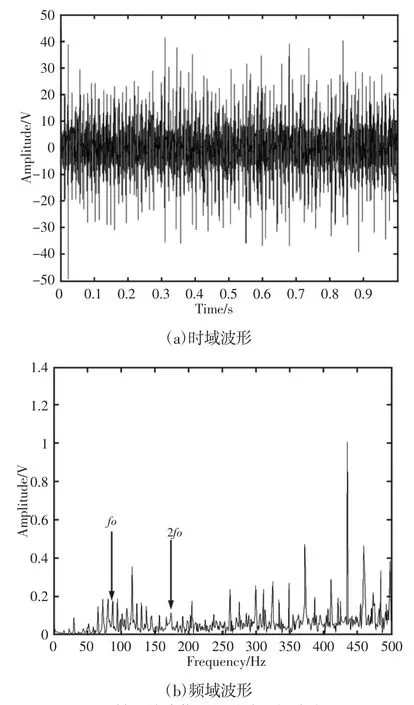
图7 轴承故障信号的时域和频域波形Fig.7 Time-Domain Diagram and Frequency-Domain Diagram of the Fault Bearing Signal

图8 分解后模式分量标度指数分布图Fig.8 Scaling Exponent Distribution of Each Mode Component of the Fault Bearing Signal

然后对含噪模式分量进行降噪处理，对重构获得降噪处理的实测信号，最后进行频谱分析，其结果，如图9所示。通过图9可以发现转频fr及二倍频2fr，外圈故障频率fo及其二倍频至五倍频都可以准确识别，因此可以判断为轴承外圈故障，这与实际的结果相一致。同时，对比图7（b）和图9，可以发现提出的方法具有明显地优势。