V2V通信同步动力分级的车辆纵向队列研究

郭国法，雷嘉豪，张开生

（陕西科技大学 电气与信息工程学院，陕西 西安 710021）

1 引言

随着道路交通的发展，公路通行容量已逐渐趋于饱和，成为制约道路运输的主要因素之一。在保持相同速度水平的情况下，减小车辆行驶间隔可以有效的增加道路容量，缓解交通压力[1]。而要减小车辆行驶的间隔，就对车辆纵向的跟随性能及安全保障提出了更高的要求。如何同时兼顾车辆安全性和道路通行效率是当前很多研究中都会面临的问题[2-3]。此外，将小间距跟随行驶策略应用于重型货运车辆的行驶过程中，可以显著降低气动阻力，从而降低燃油消耗和排放[5]。

当前已被应用的自适应巡航控制ACC可以通过对车辆间距和相对速度的测量，使后车能够自动跟随前车行驶。然而，此类通过传感器监测车辆间距或速度的传统控制方法应用在较小行驶间隔时会放大上行方向的干扰[6]，从而造成队列跟随性能降低或进一步导致系统不稳定。

基于这些问题，并考虑实际交通中车辆性能存在差异的情况，研究了一种新的纵向队列跟随控制方法，并对结果进行了仿真分析及总结。

2 协同式自适应巡航（CACC）分析

V2V通信是近年来出现的一种通过专用短程通信（Dedicated Short Range Communications，DSRC）连接车辆应用的标准通信协议。其在5.9GHz的带宽上运行，频率为75MHz[7]。

目前大多数基于V2V协同的ITS（Intelligent Transport System）应用都集中在避免碰撞及提高行车安全性上[8]，但将市面上的ACC系统与V2V通信结合，构成的协同自适应巡航（Cooperative Adaptive Cruise Control，CACC）系统具有很大改善交通流量容量和平滑度的潜力，从而增加公路的通行容量。通过引入V2V通信，车辆不仅可以通过雷达获取前车信息（ACC中的方式），由于可通过通信获取超视距的前车及事故信息，还可大幅降低由前车的速度变化引起的振荡。CACC的队列跟随行驶模型，如图1所示。

图1 CACC的队列示意图Fig.1 CACC-Equipped String of Vehicles

一个由m个不同车辆组成的纵向均匀队列如图所示，其中i为相应的车辆编号，di为车间距离。队列跟随的理想结果是在不影响安全性的情况下尽可能的保持较小的车间距离di，同时实现队列整体的稳定，即由引导车辆运动信息的突然改变引起的扰动效应会在队列内向后传递的过程中逐级衰减。

2.1 CACC控制器结构

CACC控制器的设计取决于车辆信息流的拓扑结构。拓扑结构确定了一个队列之中车辆之间的协同方式。信息流拓扑的主要类型在文献[9]中进行了总结，主要包括前向跟随（Predecessor Following，PF），含引导车辆的前向跟随（Predecessor-leader Following，PLF）和双向跟随（Bidirectional，BD）。

采用含引导车辆的前向跟随的拓扑结构。其中跟随车辆获取来自其正前方车辆及队列引导车辆的信息。此类拓扑结构下的控制器由反馈（ACC）和前馈（V2V）两部分组成。系统框图，如图2所示。前馈和反馈输入均可视为车辆动力学的输入信号。相对于传统的ACC控制通常为简单的PD或PID，CACC控制器中还加入了对无线通信信号的处理。

图2 含引导车辆的前向跟随拓扑结构的控制结构Fig.2 Control Structure of One Vehicle in CACC Platoon with PLF Information Topology

CACC作为前置的附加部分以前馈方式引入。反馈信号模块Hi（s）=1+h用来实现第三节中给出的间距策略。构成ACC部分的反馈控制器CACC是作用于车辆自身监测数据（如使用雷达）的传统控制器，以达到期望的目标。其中前馈控制器的输入Cz为车辆动力分级差。

2.2 含车间通信的车辆纵向误差跟随模型

以车辆位置，速度和加速度为状态变量的车辆纵向动力学线性化模型的状态空间表示如下：

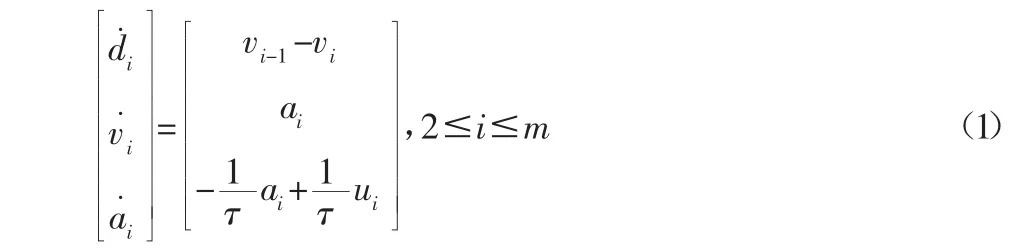
式中：di=qi-1-qi-Li—车辆i与i-1之间的距离，其中qi和qi-1分别是车辆i和i-1的尾部位置；Li—车辆的长度；vi、ai—车辆的速度和加速度。

此模型对应的车辆控制器由高级控制器和低级控制器组成，高级控制器根据输入得出系统期望信息，低级控制器以期望信息为输入调整车辆动力输出。

定义动态误差：

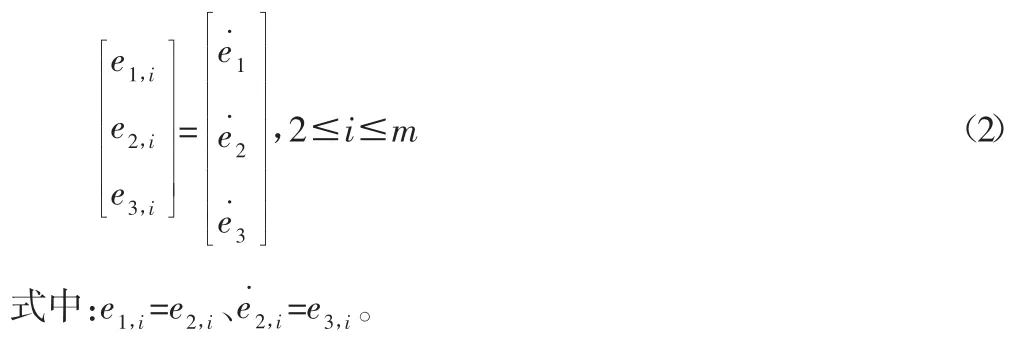
此处低级控制器将车辆加速度ai调节到输入期望加速度ui，τ为受控车辆的动力学时间常数。在研究中，期望间距策略分为恒定时间策略和恒定间距策略[11]，其中恒定时间策略对应控制器结构易于实现，应用更为广泛。采用恒定时间间隔策略：

式中：dr，i—车辆i和i-1之间的期望距离；h—间隔时间常数，其表示当ri=0时，第i辆车到达与i-1辆车相同位置的时间；ri—停顿距离；vi—车辆的速度。这种间距策略有利于提高队列的稳定性[11]。

控制中的主要目标是调节距离误差：

式中：si（t）—车辆i的位置，考虑到这个目标在实际中很难实现，即只有在前车以恒定的速度运行，ai=0时才能满足。由e3，i=e¨i及式（1）、式（4）可得出：

通过与前车的无线通信获得前馈项ui-1，这就使系统需要加入V2V通信，h为式（3）中的时间间隔。

由式（1）、式（2）、式（3）、式（4）、式（5）可以得出基于误差的四阶跟随模型为：

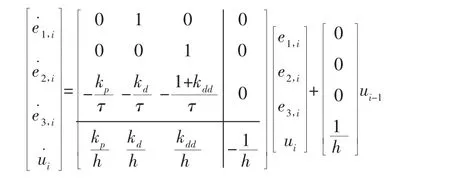
将与前车无线通信获得的前馈项ui-1替换为前后车动力及制动输出的差异信息，通过队列跟随时引导车辆车速变化的不同，将车辆纵向跟随过程分为两种情况进行控制。

3 车辆行驶性能分级

在真实道路通行中，不同车辆车型之间的动力及制动水平差异较为明显，车辆在进行单一或队列跟随时不便于对动力输出进行控制，为了减小不同车辆之间的性能差异对动力同步带来的负面影响，采取对不同车辆进行动力分级的方法。

3.1 动力分级方法

车辆的动力分级包括两方面，首先是将车辆自身能够输出的动力强弱Ci进行不同层次的分级，其次是将车辆总体的动力输出水平在所有车辆中所处的位置Ce进行分级。通过结合车内动力分级Ci和整体动力评级Ce对车辆的动力输出做出最终评估Cz，整体采用特殊的模糊化处理方法。

3.2 模糊化处理

将车辆的动力水平进行模糊化，首先将车辆内的动力输出Ci分为“极弱”、“弱”、“较弱”、“中等”、“较强”、“强”、“极强”7个模糊子集：（NB，NM，NS，Z，PS，PM，PB）。将车辆总体的动力输出水平 Ce分为“弱”、“较弱”、“中等”、“较强”、“强”5 个模糊子集：（NB，NM，Z，PM，PB）。模糊规则推理，如表 1所示。其与常规的模糊推理方式（IF X and Y then Z）有所不同，具体如下：

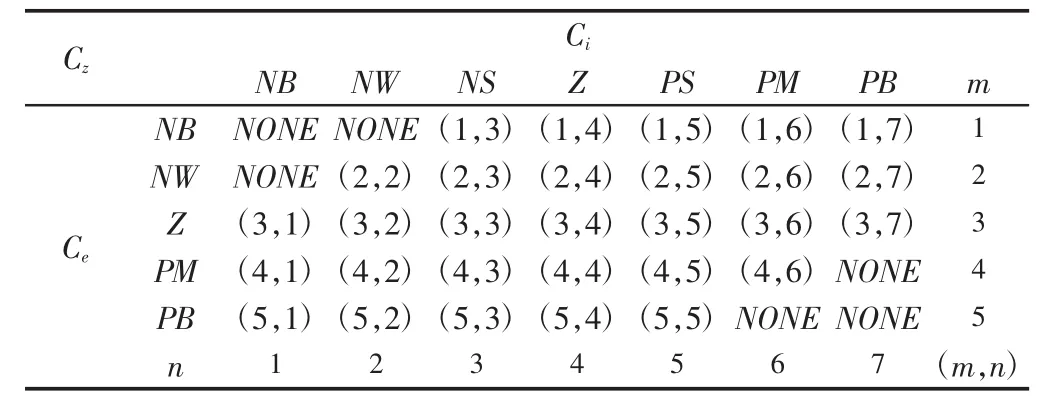
表1 模糊规则Tab.1 Fuzzy Rules

在表1中，车辆动力的最终评估Cz可由不同的m及n值组合而成 C（m，n），即：

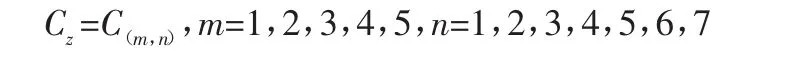
其中动力匹配关系为：C（m，n）=C（m-1，n+1），m＞1，n＜7；

这里将 C（m，n）与 C（m-1，n+1）称为同级，C（m+1，n）、C（m，n+1）比 C（m，n）大一级，C（m+2，n）、C（m，n+2）、C（m+1，n+1）比 C（m，n）大两级，以此类推。

考虑到动力同步中的合理性及实际因素中的情况，将动力最弱及最强共6个匹配值从匹配规则中去除，即：

C（m，n）∉C（1，1），C（2，1），C（1，2），C（5，6），C（4，7），C（5，7）；

动力匹配完成后，不同的车辆之间可通过匹配规则计算出相似的动力输出特性。此外，其制动性能Bz同样采用与Cz相似的模糊分级处理方式，此处不再详述。

4 跟随间距控制

4.1 间距调节方法

间距控制过程由两部分组成，分别为期望间距保持以及安全间距控制。加速时通过V2V通信，将跟随与被跟随车辆之间的动力输出情况Cz进行对比。结合第3节中的动力分级匹配规则，以κ（文中κ取1）为阈值，若ΔCz＞κ，则通过V2V同步直接作用于后车低级控制器，调整车辆动力，使跟随车辆与被跟随车辆之间的动力输出保持同步。若ΔCz≤κ，则通过传统的基于误差调节的方法进行调整。间距调节流程图，如图3所示。

制动控制过程与加速控制相似，同样通过V2V通信比对制动分级Bz，不过同步条件变为ΔBz＞ξ（文中阈值ξ取0）。

基于第二节中的分析可知，通过V2V同步控制的方法属于基于前馈的开环控制，其自身并不能进行误差调节，还需通过基于车头传感器的反馈控制修正同步过程中所产生的误差，从而确保车辆之间的安全间距。

图3 间距调节流程图Fig.3 Spacing Adjustment Flowchart

4.2 安全间距分析

安全间距即车辆在前后跟随行驶过程中所能实现的最小间距，采用相对距离制动方式下的安全间距模型，在安全间距模型中，设τd为前车与后车开始加速或制动时刻的差值，并且在该段时间内后车继续保持当前状态行驶。以前车减速时为初始时刻，则相对距离制动方式下的安全车距为：

式中：Df、Db—前后车的行驶距离；Δd—车辆之间的安全间距；ΔD—保证安全运行所需的安全裕量。具体计算方法如下：

式中：vf（0）、vb（0）—前后车减速时刻的初速度，计算方法为：

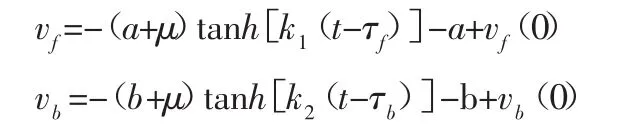
式中：k1、k2—每辆车的控制策略系数，数值不同时所采取的控制策略不同；τf、τb—相应的时间常数；Tf、Tb—前车与后车开始减速至停车的行驶时间；a、b—大于0的常数，可由前后车的初始速度及目标速度计算得出；μ—大于0的微小增量常数。

分析τd的出现原因可知，其主要由雷达扫描间隔τσ，后车测控系统响应时间τω及前车动力响应时间τλ（仅在前车由人驾驶时）组成：

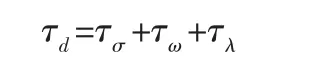
而在相对距离制动安全间距模型中加入V2V同步策略之后，基于雷达测距的反馈控制逻辑发生了改变，系统的控制输入不再只依赖雷达测量到的间距误差，从而雷达扫描间隔τσ的存在对系统的影响进一步减小。此外V2V同步将直接作用于系统的低级控制器，故后车测控系统响应时间τω也会相应降低。此时前后车的制动差值：

式中：τρ—V2V的信息通信延时，由于V2V系统自身的硬件及通

信标准，将其加入系统造成较小的负面影响。故使用V2V

同步后，前后车的制动时刻差值。

由以上可知，车辆行驶时的安全间距Δd在很大程度上取决于τd的大小，降低τd可以有效的减小车辆跟随时的安全间距，从而提高道路的通行效率。由于车辆自身动力系统延时的存在，在被跟随车辆由人驾驶时，此方法对安全间距的优化作用将会更加显著。

此外，在V2V同步动力和制动输出的过程中，由于可能会受各种随机因素的影响（如路面打滑或风速突然发生变化等），系统有极小的可能会出现在间距调节的过程中车辆间距小于安全间距的情况。针对此种情况可能存在的安全隐患，系统默认在车辆间距di≤δ（根据安全间距大小获取）时立刻停止V2V同步，重新通过位于车头的测距传感器进行反馈控制，待车辆间距回到正常范围（di≥δ）时，重新使能并启动V2V同步。

5 仿真实验

系统仿真通过MATLAB完成，车辆跟随仿真过程由4辆车构成，包括1辆引导车辆和3辆跟随车辆，4辆车依次首尾跟随排列。车辆的加速及制动响应采用式（6）所示的二阶响应模型：

每辆车都有不同的参数，仿真中的车辆参数采用文献[11]中从实际实验中测量得到的车辆加速及制动参数，其中一组参数，如表2所示。

表2 加速和制动模型参数Tab.2 Accelerating and Braking Model Parameters

在系统仿真时，为了突出主要问题，暂时忽略V2V通信中可能存在的数据丢包及干扰。其中头车以图4中类正弦曲线方式变速运动，通过对比车辆在传统方法下与这里方法下的纵向队列跟随行驶过程，来验证方法的效果及可行性。

实验结果，如图4所示。

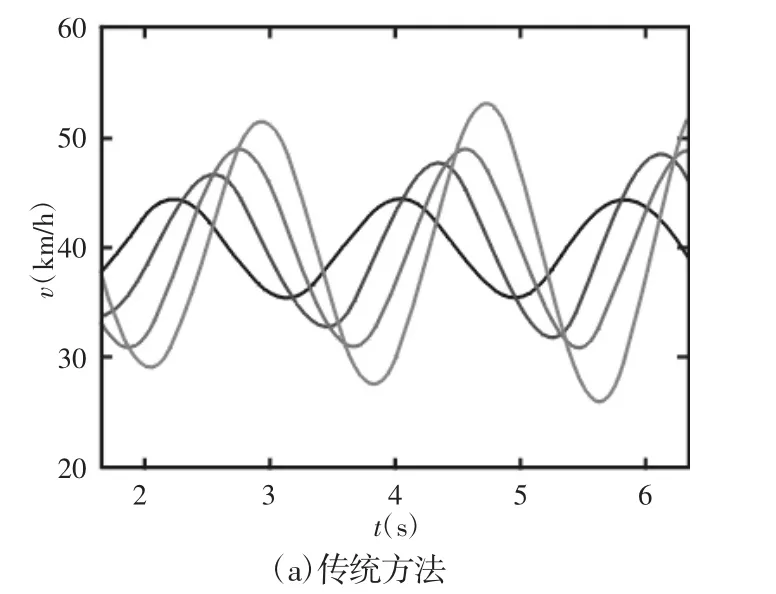
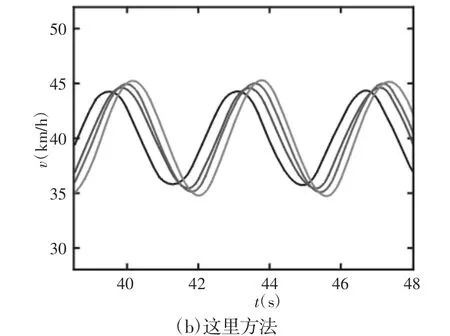
图4速度响应：（黑色-灰色）车辆1-4Fig.4 Velocity Response：（Black-Light Grey） Vehicle 1-4

图4 （a）和图4（b）显示了传统的基于车头传感器的车辆纵向队列跟随结果和基于V2V通信和动力分级的车辆协同式跟随的测试结果。两幅图都显示了部分测试轨迹中所有4辆车的速度响应，其中引导车辆的速度变化相同。图4（a）中队列末尾车辆的最大速度（在所示的时间间隔内）为52.7km/h，而图4（b）中则为46.1km/h，末尾车辆的最大速度与第一辆车的最大速度差值越大，则越不利于车辆间距稳定的保持。队列启动过程中末尾车辆至引导车辆之间的距离，如图5所示。相邻车辆静止时的初值为2m。引导车辆制动时，如图6所示。引导车辆及队列末尾车辆的制动过程，其中引导车辆从0时刻开始制动。

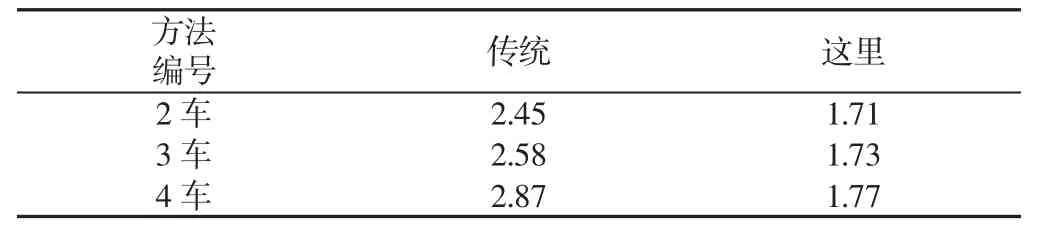
表3 行驶过程中最大加速度绝对值（m/s2）Tab.3 Absolute Maximum Acceleration（Vehicle 2-4）

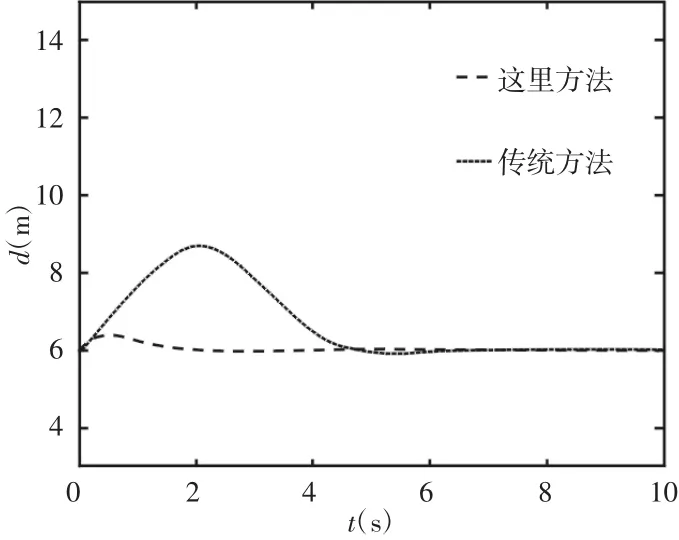
图5 启动过程中末尾车辆至引导车辆的距离Fig.5 Distance from Leading to End Vehicle During the Startup Process（Vehicle 4）

图6 引导车辆及末尾车辆的制动过程Fig.6 The Braking Process of Leading and End Vehicle（Vehicle 1 and 4）

数值仿真结果显示方法下，车辆纵向队列在行驶和启停时末尾车辆距引导车辆的最大距离，以及速度变化过程中的最大加速度绝对值均较小。实验结果在一定程度上体现出了方法较传统方法在前后车间距控制，队列稳定性方面的优势，验证了文中给出的理论分析及这里方法的可行性。

6 总结

分析了协同式自适应巡航系统的车辆纵向队列模型，从实际角度出发，针对不同车辆存在性能差异，提出并研究了一种通过V2V通信接收车辆动力输出差异信息的纵向队列跟随控制方法。通过理论分析及仿真，对传统方法及这里方法的纵向队列跟随过程进行了对比。

此外，与采用的固定时间间隔策略不同，固定间距策略在实际运用中以传统方法较难实现，在今后的研究中，期望将CACC的优势运用到固定间距策略中，探索实际交通环境下车辆纵向队列行驶时所能达到合理的最小固定间距。