基于柔性分析的配电网重构方法

郑博文，杨隽，杨承辰，鲍小锋

(玉溪供电局, 云南 玉溪 653100)

0 引 言

在配电系统中存在着两种类型的开关：分段开关(通常处于闭合状态)和联络开关(通常处于断开状态)。配电网重构通过断开某些分段开关和闭合某些联络开关等措施来改变配电网络的拓扑结构，使得新的网络拓扑结构在保证安全可靠供电的前提下，尽可能降低网络损耗、减小各节点的电压偏移、平衡各条馈线的负荷、提高供电质量等[1-5]。

现有的配电网重构方法往往以经济性为目标，来求取满足安全可靠性约束的最优配置方式。文献[6]提出了基于层次分析法的配电网重构优化方法，并分别求得正常、故障和检修等不同状态下的配电网配置方式。文献[7]针对由层次分析法所构建的配电网重构优化模型，提出了相适应的遗传算法来进行求解。文献[8]在建立配电网重构优化模型时考虑了可靠性因素的影响。文献[9]提出了从技术性和经济性等方面对配电网运行水平进行评价的指标，并将其作为目标函数，采用粒子群优化算法对配电网重构问题进行求解。文献[10]在分析了配电负荷变化规律的基础上，提出了包含网络重构的配电系统运行方式优化调度策略。

目前所提出的配电网重构方法，其安全可靠性约束所构成的边界都是用刚性表达式来刻画的，即以刚性约束条件来描述配电网重构优化模型可行域的边界。实际上，由于在配电系统的规划建设阶段采取的都是滚动规划的原则，因而任何一种典型的配电网络配置方式和运行方式在安全可靠性方面都有一定的冗余性。采用刚性的边界固然能够保证所求得的最优解严格地满足安全可靠性的要求，但也可能使得优化结果过于保守而降低配电网运行的经济性。另一方面，随着分布式能源资源的大量接入和主动配电网的进一步发展，由传统的以刚性优化为基础的配电网重构方法所给出的结果往往缺乏灵活性，难以应对各种不确定性因素。

为了更为全面地兼顾经济性与安全可靠性的要求，提出了一种基于柔性分析的配电网重构优化建模方法，其特点在于通过引入柔性参数来协调处理配电网运行的多个目标之间的联系，使得所获得的最优解能够达到综合最优。为了求解所建立的用于配电网重构的混合整数非线性优化模型，采用了改进的混合蛙跳算法，其保留了混合复杂进化算法与粒子群算法的特性，具有较强的全局寻优能力。

1 智能电网中的柔性分析方法

在智能电网的研究领域存在着大量的优化问题，其所建立的优化模型往往都是刚性的。为了克服刚性优化建模方法所存在的结果偏保守和缺乏灵活性等缺陷，文献[11-12]提出了智能电网中的柔性分析方法。

1.1 智能电网中的柔性概念

一般地，基于刚性分析而建立的优化模型可以表示成如下的形式：

minf(x,u)

(1)

式中x,u分别是状态变量和控制变量。可见，由等式约束集合与不等式约束集合所共同构成的优化模型可行域的边界是刚性的。

式(1)中的约束条件表达式可以通过引入柔性参数而表示成如下的形式：

(2)

式中εg和εh分别是等式约束和不等式约束的柔性参数，柔性参数的存在使得优化模型的可行解为了达到综合最优可以适当地越过传统的刚性边界。因此，柔性参数的大小能够反映最优解的灵活性程度。

1.2 柔性综合优化模型

柔性分析方法本质上是通过适当地降低优化模型可行解的安全可靠性而更大程度地提高其经济性，以达到综合最优。

针对式(1)所表示的传统刚性优化模型，其对应的柔性综合优化模型如下：

max(δf+δg+δh)

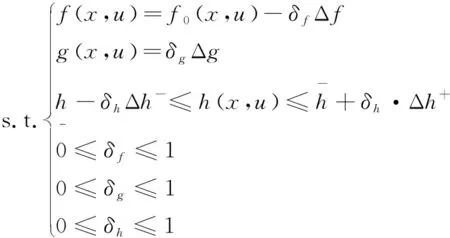
(3)

式中δf,δg,δh分别是对应于目标函数、等式约束和不等式约束的柔性参数；Δf,Δg,Δh+,Δh-则分别表示目标函数、等式约束和不等式约束所能允许越限的最大值；f0(x,u)是由式(1)所表示的传统刚性优化模型目标函数的最优值，将其作为柔性综合优化模型经济性函数的初始值；柔性综合优化模型的总目标是最大化(δf+δg+δh)，其相当于允许可行解通过适当地越过安全可靠性约束的刚性边界，来换取经济性的较大提升，这种处理方式协调了多个目标之间的联系并且提高了优化结果的灵活性。

2 基于柔性分析的配电网重构优化模型

建立基于柔性分析的配电网重构优化模型，首先需要确定其状态变量X和控制变量U，如下：

X=[V1,θ1,V2,θ2,…,Vi,θi,…,Vn,θn]

U=[T1,T2,…,Ti…,TNtie,S1,S2,…,Si,…,SNtie,δf,δg,δh]

式中Vi和θi分别表示第i个节点的电压幅值和相角；n是配电网络总的节点数；Ti表示第i个联络开关的开合状态，并且0和1分别表示断开状态和闭合状态；Si表示与联络开关Ti构成一个环路的分段开关的编号；Ntie是联络开关的总数。

则配电网重构柔性综合优化模型的约束条件分别如下所述：

(1)经济性函数的柔性化约束

配电网重构问题的经济性函数由网络损耗给出，主要包括配电网络各条支路上的有功损耗，如下：

(4)

式中Nb是配电网络总的支路数；Ri表示第i条支路上的电阻；Ii表示第i条支路上的电流幅值。

通过引入柔性参数，将式(4)所表示的经济性函数表示成柔性化约束的形式，如下：

f(X,U)=f0(X,U)-δfΔf

(5)

式中f0(X,U)表示采用传统的配电网重构优化模型所求得的经济性函数的最优值；Δf表示配电网络损耗所能够降低的最大值；δf表示对应于网络损耗的柔性参数，其数值变化范围为[0,1]。

由式(5)可知，柔性综合优化模型能够有效地降低网络损耗，即提高配电网重构优化结果的经济性，并且提高的程度由控制变量δf给出。

(2)节点功率平衡方程的柔性化约束

配电网的运行需要满足节点功率平衡方程，如下：

(6)

式中PGi,QGi分别表示第i个节点的发电有功和无功功率；PLi,QLi分别表示第i个节点的负荷有功和无功功率；Gij,Bij分别表示第i个节点与第j个节点之间的电导和电纳；θij=θi-θj。

随着主动配电网的逐步发展，出现了越来越多的柔性负荷，即可以通过灵活地调节柔性负荷的功率大小来平滑负荷曲线，实现削峰填谷等目的。由式(6)所表示的节点功率平衡方程显然是刚性的，无法模拟柔性负荷的变化。引入柔性参数后，将式(6)表示成如下的形式：

(7)

式中ΔPLi,ΔQLi分别表示第i个节点所能够增加的负荷有功和无功功率的最大值；δLi是用来模拟第i个节点上的柔性负荷的参数，其数值变化范围为[0,1]。

(3)节点电压的柔性化约束

配电系统的运行需要保证供电质量，因而需要将各节点的电压幅值控制在一定的范围内，如下：

Vi,min≤Vi≤Vi,maxi=1,2,…,n

(8)

式中Vi,max,Vi,min分别表示第i个节点的电压幅值的上下限。

将式(8)写成柔性化约束的形式，如下：

Vi,min-δViΔVi,min≤Vi≤Vi,max+δViΔVi,max

(9)

式中ΔVi,max,ΔVi,min分别表示Vi,max,Vi,min所能够允许越限的最大值；δVi用来表示第i个节点上的电压幅值的柔性参数，其数值变化范围为[0,1]。

(4)支路潮流的柔性化约束

为保证配电系统运行的安全性，配电网络各条支路上的电流幅值需要限制在一定的范围内，如下：

Ii≤Ii,maxi=1,2,…,Nb

(10)

式中Ii,max表示第i条支路上的电流幅值的上限。

将式(10)写成柔性化约束的形式，如下：

Ii≤Ii,max+δIiΔIi,max

(11)

式中ΔIi,max表示Ii,max所能够允许越限的最大值；δIi用来表示第i条支路上的电流幅值的柔性参数，其数值变化范围为[0,1]。

(5)配电网络的辐射状结构约束

配电系统运行需满足闭环设计、开环运行的准则，因而重构后的拓扑结构必须是辐射状的，如下：

Nb=n-Nsource

(12)

式中Nsource表示电源节点的总数。

由式(1)～式(12)可得，基于柔性分析的配电网重构优化模型如下：

max(δf+δg+δh)

(13)

3 改进的混合蛙跳算法

由式(13)所表示的配电网重构柔性综合优化模型是一个涉及众多实变量和离散变量的大型混合整数非线性优化模型，这使得传统的优化方法难以对其进行求解。因此，现有文献中对于类似问题的求解采用的都是现代启发式搜索算法。针对一般的启发式算法容易陷入局部最优这一缺陷，提出了改进的混合蛙跳算法来求解式(13)，其特点是保留了复杂进化算法和粒子群算法的特点，具有较强的全局寻优能力。

混合蛙跳算法最早是由文献[13]在2003年提出的，它是一种信息共享的模因元启发式搜索算法，基于的是不同互动个体所携带的模因的进化与种群之间的全局信息交换，其中将青蛙作为携带模因的载体并描述为一个向量。每一个模因由多个模因型组成，模因型与遗传算法中基因的概念类似。混合蛙跳算法不改变每个个体的物理特性，而是使一个虚拟种群中的每只青蛙所携带的模因得到不断的进化。青蛙与青蛙之间可以交换信息，并且通过所共享的信息来实现各自所携带的模因的不断进化。模因的进化使得每只青蛙的跳跃步长发生改变，进而改变了每只青蛙的位置。混合蛙跳算法将粒子群算法作为一个局部搜索工具，并且利用了复杂进化算法和信息共享的思想，从而求得全局最优解。

混合蛙跳算法将每一个可能的解视为一只青蛙，则对于本文所建立的配电网重构柔性综合优化模型，可以将每只青蛙定义为：

Ui=(Ui1,…,Uid,…,Uiz)=

[T1,T2,…,TNtie,S1,S2,…,SNtie,δf,δg,δh]

所提出的改进混合蛙跳算法的求解步骤如下：

步骤1：随机生成一个虚拟的种群，使得其中包含k只青蛙；

步骤2：对于所生成的虚拟种群，计算其对应的目标函数值。根据适应度对k只青蛙进行降序排列；

步骤3：将k只青蛙分成p个模因组，使得每个模因组包含q只青蛙。分组的方式是：将第一只青蛙分入第一个模因组，将第二只青蛙分入第二个模因组，第p只青蛙分入第p个模因组，将第p+1只青蛙分入第一个模因组……。对于第j个模因组，将具有最好适应度的青蛙记为Ub,j，将具有最坏适应度的青蛙记为Uw,j。将具有全局的最好适应度的青蛙记为Ug；

步骤4：使每个模因组中具有最坏适应度的青蛙得到进化，具体过程如下：

首先，在Ub,j(j=1,2,3,…,p)中随机地选取一只青蛙Ubr使得Ug≠Ubr。其次，可以计算出一个新的向量UDj，如下：

UDj=[ud,1,…,ud,2×Ntie,…]=Ug+β(Ubj-Ubr)

Ub,j=[ubj,1,…,ubj,2×Ntie,…]=

[Tbj,1,Tbj,2,…,Tbj,Ntie,Sbj,1,Sbj,2,…,Sbj,Ntie,δbj,f,δbj,g,δbj,h]

Ug=[ug,1,…,ug,2×Ntie,…]=

[Tg,1,Tg,2,…,Tg,Ntie,Sg,1,Sg,2,…,Sg,Ntie,δg,f,δg,g,δg,h]

Ubr,j=[ubr,1,…,ubr,2×Ntie,…]=

[Tbr,1,Tbr,2,…,Tbr,Ntie,Sbr,1,Sbr,2,…,Sbr,Ntie,δbr,f,δbr,g,δbr,h]Uw,j=[uwj,1,…,uwj,2×Ntie,…]=

[Twj,1,Twj,2,…,Twj,Ntie,Swj,1,Swj,2,…,Swj,Ntie,δwj,f,δwj,g,δwj,h]

其中，β是一个在区间(0.1,1.2)内的常数。最后，具有最坏适应度的青蛙的位置将被更改为：

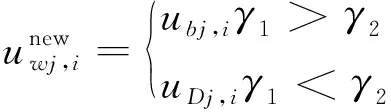
步骤5：将上述步骤迭代若干次；

步骤6：将分组的方式重新打乱；

步骤7：如果未满足终止条件，则返回步骤2；否则，终止求解过程。

4 算例分析

采用IEEE 33节点配电系统来验证所提出的配电网重构柔性综合优化模型的正确性和有效性。该系统的电压等级是12.66 kV，它有32个负荷节点、32个分段开关和5个联络开关，该系统的拓扑结构图和具体参数见文献[14]。其中，初始状态下处于断开状态的开关是：s33，s34，s35，s36和s37；初始状态下处于闭合状态的开关是：s1～s32。

表1 是传统的基于刚性分析的配电网重构方法所得到的优化结果。

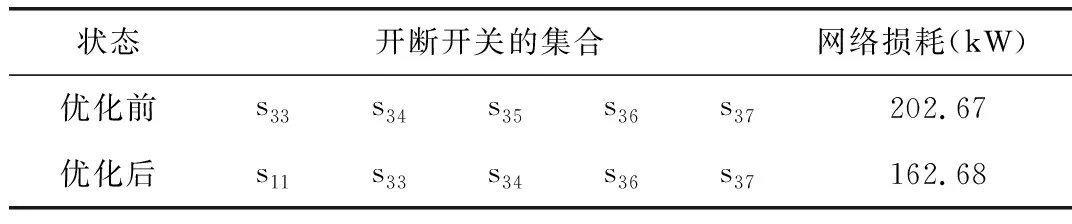
表1 基于刚性分析的配电网重构方法的优化结果Tab.1 Optimization result of distribution network configuration method based on rigid analysis

对IEEE 33节点配电系统，建立基于柔性分析的配电网重构综合优化模型，并采用改进的混合蛙跳算法进行求解，所得的优化结果如表2所示。其中，f0(X,U)的值取为162.68 kW；假设配电网的平均线损率为10%，则Δf的值可以取为25 kW。需要指出的是，Δf取值的大小实际上反映了配电系统运行人员的风险偏好。即如果运行人员根据长期的运行经验认为该配电系统的安全可靠性冗余较大，那么Δf可以取相对较大的值；否则，Δf应该取相对较小的值。

表2 基于柔性分析的配电网重构方法的优化结果Tab.2 Optimization result of distribution network configuration method based on flexible analysis

由表1和表2可以看出，所提出的配电网重构柔性综合优化方法比传统的方法所得到的网络损耗有较大程度地降低(从162.68 kW降低到了139.53 kW)。换言之，采用所提出的方法能够在保证安全可靠供电的前提下较大程度地提高配电网络运行的经济性。

此外，为了比较传统方法和所提出方法优化结果的安全可靠性水平，需要求得两种方法所给出的各节点电压幅值，并对比如下的统计指标，对比结果如表3所示。需要指出的是，由于各节点电压的幅值都采用的是标幺值，因此表3中的单位也是以标幺值的形式来表示。

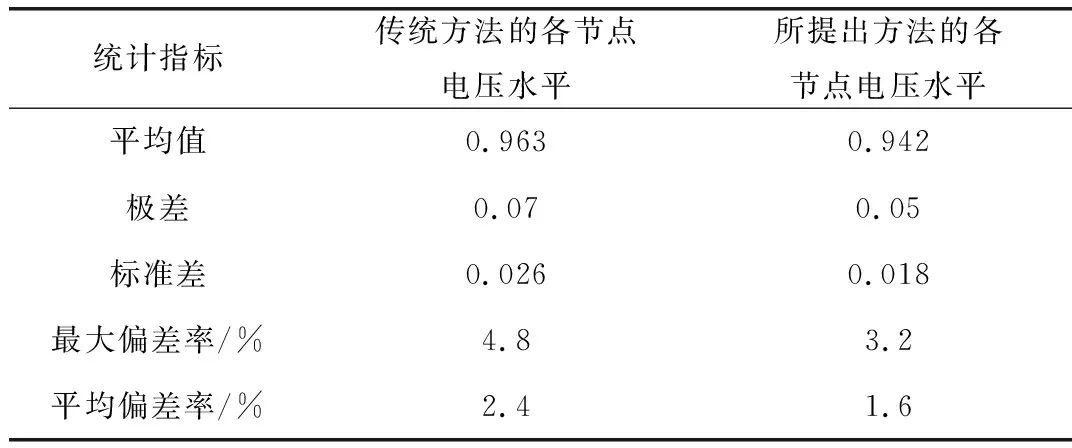
表3 两种优化模型所得结果的各节点电压水平Tab.3 Nodal voltage level of optimization results of two optimal models

极差：RV=Vk,max-Vk,min

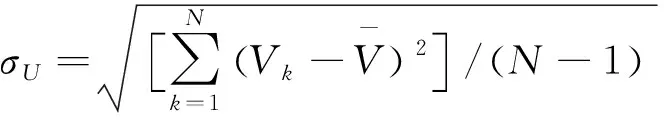
由表3可以看出，与传统方法相比，所提出方法所求得结果的各节点电压水平偏离额定值较大。这表明配电网重构的柔性综合优化方法本质上是通过适当地降低供电质量而更大程度地提高其经济性，以达到综合最优。

5 结束语

针对现有的基于刚性分析的配电网重构方法的不足，提出了一种基于柔性分析的配电网重构优化建模方法，其特点在于通过引入柔性参数来协调处理配电网运行的多个目标之间的联系，使得所获得的最优解能够更为全面地兼顾经济性与安全可靠性的要求。为了求解所建立的用于配电网重构的混合整数非线性优化模型，采用了改进的混合蛙跳算法，其保留了混合复杂进化算法与粒子群算法的特性，具有较强的全局寻优能力。