基于改进人工鱼群算法的互感器Jiles-Atherton模型参数辨识*

林国营，宋强，潘峰，肖厦颖，李开成，王凌云

(1.广东电网有限责任公司电力科学研究院，广州 510000； 2.华中科技大学 电气与电子工程学院 强电磁工程与新技术国家重点实验室，武汉 430074)

0 引 言

电磁式互感器多使用非线性铁磁材料制作。为了开展仿真平台下的电磁式互感器特性研究，使仿真效果尽可能地接近实际情况，需要对试验互感器搭建精确的铁芯磁滞模型。描述磁滞现象的理论模型有Lucas、Jiles-Atherton模型(下文均简称为J-A模型)等。其中J-A模型因其控制参数较少而被广泛应用在铁磁材料的磁滞建模与仿真中。J-A模型各方程与参量均具有明确的物理意义，可以准确描述铁芯磁滞回线的非线性关系。通过求解J-A模型的微分方程组便能够得到与真实情况拟合度较高的B-H曲线，从而实现互感器的精确建模。

在难以直接获取方程参数的场合中经常需要使用数学方法对参数进行辨识，即通过求解最优拟合参数来逼近理论参数。若求解结果的误差足够小，则认为拟合参数已经精确到可以取代理论参数[1]。J-A磁滞模型的参数虽具有实际意义，却难以通过实测直接得到，所以要对其进行准确可靠的参数辨识。

目前应用于J-A模型参数辨识的常用算法主要是一些基于仿生学的智能优化算法，如遗传算法、粒子群算法、模拟退火算法等，但是对于处理复杂的优化问题，单一的智能寻优方法往往存在显著缺陷，不利于获取精确的全局最优解，如模拟退火算法对初始温度、温度衰减系数等参数设置较为敏感，且搜索后期收敛速度较慢。

近年来，大多数文献采用多种算法相结合的方式来寻找J-A模型的最佳参数组合。文献[2]使用了粒子群算法(PSO)结合Simulink动态仿真的方法来拟合J-A磁滞回线模型，并获取相关参数。该方法虽表现出较好的鲁棒性和收敛性，但是算法复杂度较高，运行时间较长。文献[3-4]采用神经网络和遗传算法相结合的方法，先使用神经网络算法训练寻优函数，再通过遗传算法进行极值寻优，相比单优化算法达到了较高的拟合精度，但也导致了算法时效性不足。文献[5]提出了一种结合混沌优化、遗传算法和模拟退火算法的混合优化方法，牺牲算法简便性以获取较快的收敛速度。文献[6]采用模糊控制方法获取动态反馈系数进行蛙跳算法步长修正，减小了原本蛙跳算法的随机性且具有一定的自适应能力，但对整体收敛品质提升不高。

使用一种基于变步长人工鱼群和并行模拟退火算法的改进混合算法进行电磁式电流互感器铁芯J-A模型的关键参数辨识。人工鱼群算法是一种通过模拟鱼群行为进行随机搜索的智能优化算法，能够快速将搜索域缩小至全局最优解的附近，但是该算法盲目性较大，导致后期寻优难以获得更为精确的结果，同时减慢了寻优速度。而基于Meteopolis准则的模拟退火算法在搜索初期温度较高时以较高的概率接受差解，从而不易陷入局部最优解；在温度较低时，允许差解的概率变低从而使搜索更为精确。本文提出的改进混合算法，在寻优前期利用人工鱼群算法快速接近全局最优解，并引入变步长因子减小算法的随机性；再使用模拟退火算法在较小范围内进行局部搜索，同时利用并行控制策略进行多线程运算。改进混合算法解决了鱼群算法效率较低以及退火算法难以大范围搜索的问题，能有效提高J-A模型参数辨识的时效性与精确度。

1 互感器Jiles-Atherton模型

互感器等效模型的准确性和有效性，关键在于铁芯磁滞现象的物理描述与数学表达[7]。目前，描述磁滞现象较为经典的模型有Lucas模型和Jiles-Atherton(J-A)模型等[8-10]。其中J-A模型所需辨识的参数较少，实现起来较为方便，PSCAD等多款电力仿真软件中都嵌入了基于J-A理论的互感器等值模型。该模型适用性广且便于扩展研究。

在J-A理论模型的基础上又出现了多种改进策略，不同文献对于J-A理论的引用和转述也不尽相同，采用文献[7]提出的改进J-A模型作为互感器建模仿真的基础。

磁化强度M、磁场强度H与磁通密度B之间的关系为：

B=μ0(H+M)

(1)

式中μ0=4π×10-7为真空磁导率。

根据能量守恒原理得到能量方程式：

(2)

式中He表示有效磁场强度；α为表征磁畴内部耦合的平均场参数；Man为无磁滞磁化强度，即理想材料的磁化强度；Mirr表示M中的不可逆磁化分量；Mrev表示M中的可逆磁化分量。He、Man、Mirr和Mrev的表达式如下：

He=H+αM

(3)

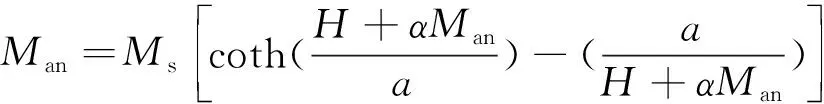
(4)

M=Mirr+Mrev

(5)

Mrev=c(Man-Mirr)

(6)

再由式(5)和式(6)得到：

Mirr=(M-cMan)/(1-c)

(7)

将式(3)～式(7)带入能量守恒式(2)，可得：

(8)

式中δ是一个符号函数，当dH/dt>0时，δ=1， dH/dt<0时，δ=-1。

为了消除J-A的非物理解，对式(8)进行修正，修正后的J-A模型方程为：

(9)

(10)

(11)

上述公式中修正系数β通常取0.96。Ms、a、α、c、k为J-A模型中待求的5个未知参数，都具有明确的物理意义:Ms代表饱和磁化强度，a为朗之万函数参数；α为磁畴内部耦合的平均场参数；c为可逆磁化系数；k为损耗系数。因此,对于每种铁磁材料，其参数是确定的，且能准确反应该材料的磁化特性。

2 基于改进混合算法的智能寻优算法

由上一节描述可知，互感器J-A模型参数辨识问题可以看作一个计算量非常庞大的非线性方程组求解问题，群体智能优化算法因其在大数据环境下良好的计算能力而常被应用于解决此类问题。

2.1 人工鱼群算法

人工鱼群算法(Artificial Fish Swarm Algorithm， AFSA)思路来自于自然界鱼群总是朝向食物浓度高的地方移动这一特征[8]，将计算模型的目标函数作为搜索目标，模拟鱼群的行为方式，在一定范围的搜索域中寻找最佳目标及其对应的控制变量参数。相比于其他的智能寻优算法，AFSA只将寻优目标值作为唯一辨识条件，对约束范围的依赖性小，且对初值与参数设定不敏感，适应性广[9]；引入变步长因子的AFSA，其移动步长根据条件灵活应变，具有自适应能力，整体收敛速度较快。

将计算模型的关键参数作为人工鱼的位置坐标，若存在k个模型参数，那么在共有N条人工鱼的鱼群中，第i条人工鱼位置Xi=(x1i,x2i,…,xki)，其中xki为第k个参数的取值。将这些参数带入计算模型和目标函数中得到因变量Yi作为该位置的食物量(即寻优目标)，每次迭代通过模拟各种鱼群行为来更新人工鱼的位置，使得鱼群朝向食物量最大的区域聚集[10]。以求极大值问题为例，AFSA三种典型的人工鱼行为描述如下：

(1)觅食行为。人工鱼当下位置为Xi，在其感知范围内随机另选位置Xj，比较这两个位置的食物量Yi和Yj，若Yj>Yi，则向Xj方位前进一步。否则重新选择位置Xj，若反复试验一定次数后Yj仍不能超出Yi，则判定其不满足前进条件，人工鱼随机移动一步；

(2)聚群行为。设第i条人工鱼Xi当前可视范围内的伙伴数量及中心位置分别为nf和Xc，当Yc/nf>δYi(δ为拥挤度)时，表示伙伴中心的食物密度较高，则Xi朝该方位移动一步，否则执行觅食行为；

(3)追尾行为。类似于聚群行为，记当前可视范围的伙伴中Xj的食物量Yj最大，如果Yj/nf>δYi，表明伙伴Xj所处位置具有较多食物，则Xi朝该方位移动一步，否则执行觅食行为。

虽然AFSA前期能较快收敛，缩小搜索域的约束范围，但其在小范围内的精确检索却较为缓慢，无法快速获取高精度要求下的最优目标值[11]。这一缺陷在处理复杂优化问题时表现的尤为明显。该算法一旦进入到目标值更迭不明显的搜索域时，AFSA的收敛速度大幅减慢，难以逼近全局最优解。总的来说，AFSA后期较差的搜索性能抑制了算法的总体寻优能力，搜索至一定精度后难以得到进一步优化，极大地减慢了运算速度，严重影响其搜索质量和效率[12-13]。

2.2 改进混合智能寻优算法

模拟退火(Simulated Annealing,SA)算法最早是由Metropolis等提出，后来逐渐发展成一种迭代自适应启发式概率性搜索算法[14]。该算法具有较高的鲁棒性且局部搜索能力强。为了使J-A模型参数辨识更加精确，尽可能地缩小全局误差，文中在人工鱼群算法的基础上引入模拟退火算法，使混合算法在前期使用AFSA进行快速收敛，后期利用SA进行局部搜索，进一步精确寻优。

SA在Metropolis准则的基础上判定是否接受搜寻优过程中的产生的新解。假设计算模型的目标函数为f(x)，自变量为x。当温度为T时，若当前解为x1，不同于x1的一个新解为x2，其目标差df=f(x1)-f(x2)，则Metropolis准则为：

(12)

如果df<0，则以概率1接受新解；否则以概率exp(-df/T)接受新解。

在人工鱼群算法中，认为食物量为鱼群寻找的目标函数，鱼群向着食物较多的方向移动。依循以上思想，将J-A模型的五个关键参数的取值作为人工鱼的位置坐标。目标函数Fitness如式(14)所示。当目标函数达到最大时，参数辨识水平最高，即互感器J-A模型与实际测量数据的拟合度最高。

(13)

(14)

在J-A模型计算量较大的应用环境下，寻优算法的消耗时长具有一定的随机性。所提出的改进算法在搜索前期对传统人工鱼群算法引入变步长因子控制其随机性，使个体选择适合的步长移动，加快人工鱼群算法在搜索前期的迭代速度；在搜索后期引入并行策略，使得模拟退火算法通过四条线程并行运算，取得不错的扩展性，且可以更快收敛。改进算法运用于J-A模型参数辨识的主流程如图1所示。

图1 基于人工鱼群和模拟退火算法的改进混合算法流程图Fig.1 Flow chart of the improved hybrid algorithm based on AFSA and SA

改进混合算法描述如下：

(1)建立Jiles-Atherton互感器磁滞回线模型：

B=f([Ms，a，α，c，k]，H)

(2)给定J-A模型参数辨识问题的约束条件，在约束条件的范围内随机对Ms，a，α，c，k五个参数取值，得到n组随机参数组合，每个随机参数组合视为一条人工鱼的位置坐标。

(3)执行变步长人工鱼群算法，流程图如图2所示。

图2 变步长人工鱼群算法流程图Fig.2 Flow chart of the variable-step artificial fish swarm algorithm

(a)初始化人工鱼群：设定个体数量n、最大迭代次数maxgen、搜索前期阈值Ymax1、定步长step；将人工鱼群记为{X1,X2,…,Xn}，对应目标函数记为{Y1,Y2,…,Yn}；

(b)执行聚群行为和追尾行为，若满足Y(X)>Yi(Xi)，则改变当前人工鱼的位置坐标Xi=Xi+rand*step*|X-Xi|，其中rand是小于1的随机数，目的是对定步长step进行自适应修正。取两种行为获取的较大目标函数值更新Yi，人工鱼随之移动到对应位置Xi；

(c)获取整个鱼群中最高的目标函数Ybest=max[Yi]，以及Ybest对应的人工鱼位置Xbest，即得到搜索至此的最佳J-A模型参数组合；

(d)若此时Ybest小于前期阈值Ymax1，则进入下一次迭代，迭代次数gen=gen+1，继续执行(2)～(3)的迭代过程，直至Ybest>Ymax1，前期搜索结束，转而进入并行模拟退火算法；

(4)进入并行模拟退火算法，流程图如图3所示。

图3 并行模拟退火算法流程图Fig.3 Flow chart of parallel simulated annealing algorithm

(a)参数初始化：初温T0，终止温度Tend，链长L，降温速率q，最大允许误差per_erro；

(b)主线程和分线程同时输入初解作为模拟退火当下温度的初始解，初解为前期搜索获取的最优解，有：S1=Xbest；

(c)主线程负责记录初始解，分线程进入温度迭代过程，根据Metropolis法则，进行1次解更新，更新后的解和初始解一起比较选出当前最优解ybest，以及对应的xbest和当前误差erro；

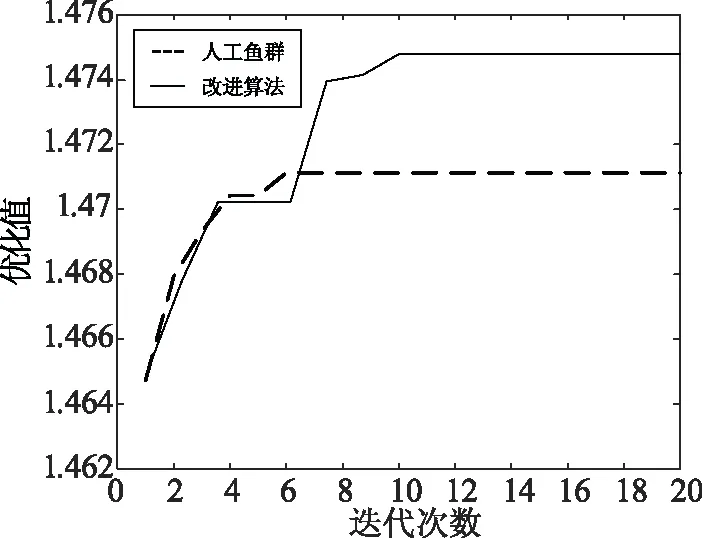
(d)若erro依然大于计算允许的最大误差per_erro，则将当前局部最优解作为主线程和分线程下一退火温度的初始解，令T0=q*T0，继续迭代步骤(c)，直至erro

(5)若全局最优值Ybest未达到后期阈值Ymax2，则令迭代次数gen=gen+1，继续执行(2)～(5)，直至Ybest>Ymax2，结束搜索，对应的参数组合[Ms，a，α，c，k]即为J-A模型参数辨识的结果。

3 改进混合算法的参数辨识及误差对比分析

为了验证上述改进混合算法的时效性和精确性，利用Matlab工具进行该算法下的J-A模型参数辨识。仿真计算程序由Matlab2016编译运行，计算机CPU型号为i7-5930K、3.5 GHz,内存为32 GB。

文章使用的实测数据来自文献[6]，J-A模型的五个参数的取值范围及理论值如表1所示。

表1 J-A模型参数范围及理论值Tab.1 The range and theoretical values of J-A parameters

实测数据为1 000组B-H值，将H带入式(1)、式(4)和式(6)，计算对应的B值，使得目标函数fitness达到全局最优解，并得到最优解所对应的五个参数a,c,k,α和Ms的值，即为辨识结果。

本节分别用粒子群算法、人工鱼群算法、以及改进混合算法对J-A模型进行参数辨识。其中鱼群算法及其改进算法均设定鱼群数为20只，最大迭代次数为20次。参数辨识结果对比如表2所示。

表2 参数辨识结果及计算时间对比Tab.2 Comparison of the identified J-A parameters value and computation time

改进混合算法和鱼群算法的相对理论曲线的拟合情况对比如图4所示，可发现两种方法的曲线拟合效果均较好，几乎无可视误差。

图4 B-H曲线辨识结果对比Fig.4 Comparison of identified B-H curve

由表1可以看出，改进混合算法的辨识精度最高，单一的人工鱼群算法精度次之，而粒子群算法精度最低，算法耗时排序则正好相反，综合来看，改进混合算法可以在最短时间内辨识出更加精确的全局最优解，参数辨识时效性和精准度均优于其他两种方法，尤其是与人工鱼群算法相比，改进混合算法的最优解相对误差减少了0.2个百分点，仅为鱼群算法相对误差的一半。

人工鱼群算法及改进混合算法收敛速度对比如图5所示。图5中明显可以看到，鱼群算法在前5次迭代时目标值优化速度较快，但从第6次迭代开始目标值停留在1.48附近不再继续增加，直至达到最大迭代次数，相对而言整体收敛速度较慢。而采用改进混合算法时，在第6次迭代后跳出鱼群算法的约束，转用并行模拟退火算法进行局部寻优，使得后期也达到了较高的收敛速度，快速收敛至第10次迭代，之后目标值稳定在1.475直至收敛结束，具有较优的搜索质量。多次使用改进混合算法进行参数辨识仿真实验可以发现，寻优迭代曲线基本一致，算法的随机性降低，收敛速度较为稳定，平均4.8次迭代即可达到前期阈值，平均11.5次可达到全局最优解。故而可设定最大迭代次数在15次以内，改进算法在300 s以内即可得出互感器J-A模型参数辨识结果，准确度高且搜索速度快。

图5 优化值进化曲线对比Fig.5 Comparison of fitness value curves

4 结束语

提出了一种基于变步长人工鱼群算法和并行模拟退火算法的改进混合算法，用于互感器J-A模型的5个关键参数辨识问题中。改进算法在搜索前期利用变步长人工鱼群算法接近全局最优解，搜索后期利用并行模拟退火算法进行进一步的局部搜索，以获取更为准确的全局最优解及其对应的参数辨识结果。建模仿真实验也验证了改进算法在较少的收敛次数下能获取更加精准的全局最优解，且计算速度不受传统算法随机性制约，稳定性较高。相比于传统的粒子群算法和人工鱼群算法，在耗时较短的情况下即可将精度提高近一倍之多，有效提升了互感器J-A模型参数辨识的效率和精度。该算法可应用于互感器特性研究的仿真实验中，能有效构建更为准确可靠的互感器模型，具有较高的实际应用价值，适用性较广。