非线性电容RLC串联电路的2次超谐共振分析

李高峰

(唐山学院 基础部，河北 唐山 063000)

0 引言

以变容二极管、参数放大器、混音器、传感器等装置设计电路时，电子元器件通常用非线性电容。詹士昌等研究了非线性RLC串联谐振电路[1]。黄偲等给出了一类非线性RLC电路的新解法及数值仿真，从而算出电路的相轨线、时程曲线、相程曲线、时幅曲线、相幅曲线、幅频曲线、相频曲线和响应周期，数值仿真显示，结果与数值积分法吻合良好[2]。丁光涛利用Lagrange力学逆问题理论和方法，构造了电感、电容和电阻三种耦合RLC电路的Lagrange函数和Hamilton函数[3]。郭晓莹等在电容耦合RLC电路中，通过改变外部信号源的频率，测量了传输到第一个RLC回路的功率随信号频率的变化关系[4]。杨志安等研究了非线性RLC电路与板和微梁耦合系统的非线性动力学问题[5-7]。潘杰等对RLC并联谐振电路进行了理论研究[8]。B.Nana等研究了铁磁磁芯电感器件的非线性，分析了在由交流电源强迫的RLC串联电路中电流的解析表达式[9]。国外学者还对非线性RLC电路动力学问题和系统产生混沌现象的条件等进行了研究[10-12]。

笔者曾对非线性电容RLC串联电路进行过主共振和亚谐共振的研究[13-15]。现本文从超谐视角，以RLC串联电路的振动微分方程为研究对象，研究非线性电容RLC串联电路系统的2次超谐共振问题。

1 RLC串联电路的振动方程

根据拉格朗日-麦克斯韦方程，可得到该系统的运动微分方程为

(1)

对式(1)进行处理，可得著名的Duffing方程为

(2)

2 2次超谐共振理论分析

弱非线性振动在非线性和阻尼项前面冠以小参数ε，可得

(3)

应用多尺度法求2次超谐共振微分方程，设

q(T)=q0(T0，T1)+εq1(T0，T1)。

(4)

将式(4)代入式(3)得到一组线性偏微分方程

D02q0+ω02q0=fcosωt，

(5)

D02q1+ω02q1=-2D0D1q0-2μD0q0-α2q02-α3q03。

(6)

方程(5)的解为

φn0(T0，T1)=A(T1)ejω0T0+BejωT0+cc，

(7)

(8)

将式(8)代入式(6)得

(9)

研究系统的2次超谐共振，引入调谐参数σ，由下式确定为

2ω=ω0+εσ，σ=o(1)。

由式(9)得消除永年项的条件为

(10)

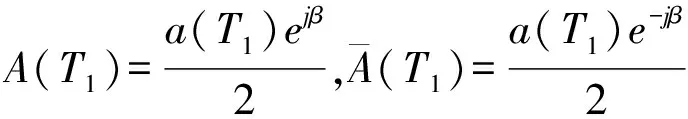
(11)

相应的一次近似解为

(12)

令式(11)中D1a=0，D1φ=0，消去φ，得到2次超谐共振的幅频响应方程

(13)

(14)

从方程(13)中解出σ为a的函数，得

(15)

3 数值实例分析

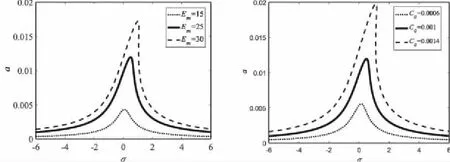
应用Matlab软件对式(13)进行计算，可以得到RLC串联电路2次超谐共振的响应曲线(见图1)，数值计算中，电子元器件的基本参数为：电阻R=15 Ω，电动势Em=25 V，电感L=15 H，线性电容C0=0.001 F。

(a)Em (b)C0

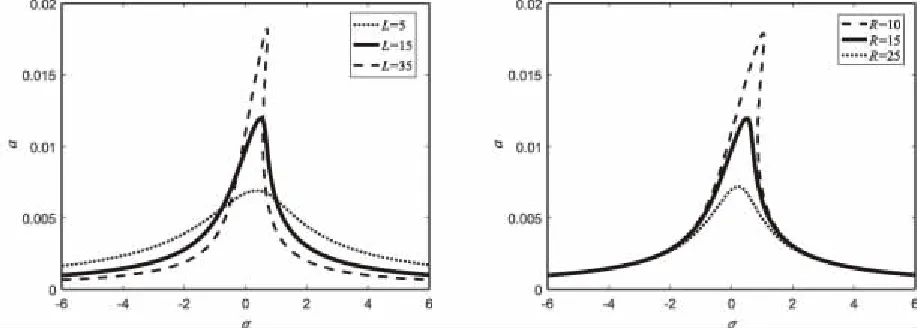
(c)L (d)R图1 系统的超谐共振响应曲线

图1中系统的超谐共振响应曲线具有跳跃现象和滞后现象。电动势作为系统的供能元件，电容、电阻和电感作为耗能元件，其数值变化时对系统振幅以及共振区域均有影响。由图1(a)到图1(c)可知，电动势、线性电容和电感增大时，系统的共振幅值均增大，且图1(a)和图1(b)的共振区域依次增大，而图1(c)共振区域随振幅的增大而变窄。图1(d)中随着电阻值的增大系统的共振幅值和区域都减小，这是因为电阻抑制系统的非线性，电阻增大时电流减弱，电路中的电荷也相应减少。

图2为调谐值变化时电动势-振幅响应曲线，电动势增大时振动幅值增大，整个电路中电流增大，电荷增多。图3为振幅随电容变化的响应曲线，随着电容的增大，振幅也增大。图4为振幅随非线性电荷系数k2变化的响应曲线，随着k2的增大，振动幅值也增大。图5为振幅随非线性电荷系数k3变化的响应曲线，随着k3的增大，振动幅值减小，但应注意的是，σ>0时曲线振幅随非线性电荷系数增大先增大再减小。综合图2-5可知，当σ>0时，随着电动势、电容、非线性电荷系数等参数的增大，RLC串联电路的响应曲线具有跳跃现象和滞后现象；在σ<0时，参数增大时系统振动幅值逐渐增加，不出现跳跃现象和滞后现象。

图2 电动势-振幅响应曲线

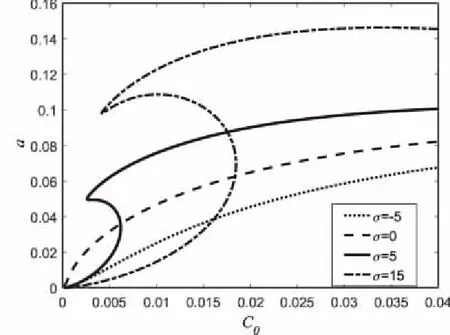
图3 电容-振幅响应曲线

图4 非线性电荷系数k2-振幅响应曲线

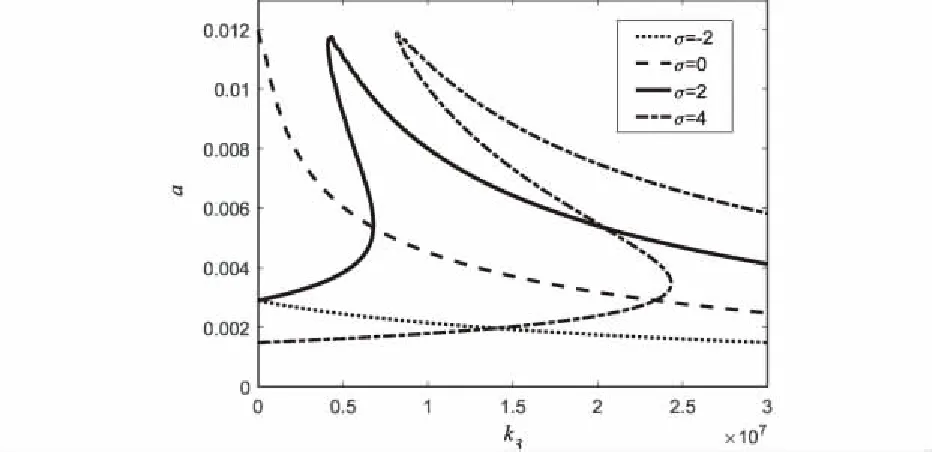
图5 非线性电荷系数k3-振幅响应曲线

图6为电阻-振幅响应曲线，调谐值越大系统的振动幅值滞后性越强，逐渐出现了跳跃现象，与图1(b)比较可知，在σ=0且电阻增大时，振动幅值缓慢减弱，最终趋于稳定。图7为振幅随电感变化的响应曲线，当调谐值增大，系统的振动幅值减小；当σ>0时，随着电感的增大系统的振动幅值减小，并趋于稳定；当σ=0时，随着电感的增大系统的振动幅值增大。

图6 电阻-振幅响应曲线

图7 电感-振幅响应曲线

4 结论

应用多尺度法得到非线性电容RLC串联电路系统2次超谐的幅频响应方程。电路中的非线性振动是由电路中的移动电荷造成的，电阻增大电路中的电流减小，同时电荷数减少，振动的振幅相应减小，此时电阻对振幅有抑制作用。当σ>0时，随着电动势、电容、非线性电荷系数k2与k3等参数的增大，RLC串联电路的响应曲线具有跳跃现象和滞后现象。