非线性时变加载系统的高频段多余力抑制方法

赵孟文，樊泽明

（1.西安航空学院陕西西安710077；2.西北工业大学自动化学院，陕西西安710072）

舵机是飞控系统中重要的伺服元件，负载模拟器是舵机在地面做性能实验的加载系统。加载系统要求模拟实际飞行器及其部件在飞行过程中所受到的包括惯性力、阻力、干扰力等在内的各种载荷，快速、准确地跟踪舵机的运动，它是一个非线性时变的伺服系统。加载过程中，由于加载设备的自身结构、机械连接，摩擦力矩、控制方法等因素的影响，系统存在着多余力，严重影响了系统的加载精度和动态性能，使系统的稳定性变差、跟随性降低。以往的多余力控制策略主要基于结构不变性原理，建立线性化数学模型，提出补偿控制策略[1]。但随着系统复杂程度的提高，非线性和不确定性因素的增多，同时对加载频率要求也越来越高，就需要更先进的且针对性强的进控制算法。

文中建立了典型加载系统的数学模型，在研究多种控制算法的基础上，提出了一种非线性时变加载系统的高频段多余力抑制方法，通过仿真及实验证明其具有很好的抗扰动性，更能适应系统的参数变化及高频加载要求[2]。

1 伺服加载系统及数学模型

1.1 系统结构简述

伺服加载系统采用伺服电机进行加载，系统结构由4部分组成：被试舵机安装台、加载系统（包括两个加载电机、扭矩传感器和旋转编码器、惯量模拟机构等）、加载台架、计算机控制系统。系统采用了大小不同的两个伺服电机同轴安装、加载，是为了满足大载荷的力矩加载及小载荷时，小角度高精确的位置控制要求。惯量模拟机构模拟舵面的实际惯量。工控机通过人机交互界面及系统控制软件，进行闭环控制与监测。根据控制算法得到控制指令，通过数据总线、D/A转换模块、功率放大，驱动伺服电机进行加载。扭矩传感器得到的反馈信号经过信号处理、A/D转换，再通过ASI总线形成闭环控制[3]。工控机控制结构如图1所示。

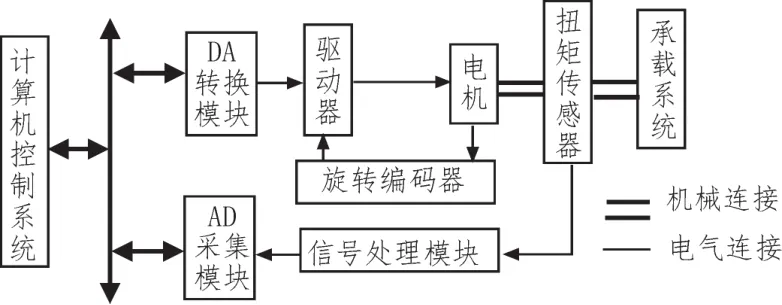
图1 工控机控制结构

1.2 系统数学模型的建立

根据设计要求，确定合理的加载方式，选用合适的加载电机可以减少中间环节的影响，提高响应速度及加载精度。研究伺服电机的内部各个电气平衡方程、电枢感应电动势微分表达式、力矩电机的电磁转矩公式、力矩电机的转矩平衡方程，经过拉式变换可得加载伺服电机的数学模型[4]。被试舵机和加载电机都是采用无刷直流电机和脉宽调制（PWM）驱动装置，力矩电机可以进行较宽范围的位置和速度控制，响应频率快，功率因数高。PWM是斩波控制方式的一种。它通过控制各个对应功率管的导通次序，来改变脉冲电压的宽度使得电机上一个周期内的平均电压得到改变，即通过改变占空比来调压。研究控制信号在系统中传递所遵循的客观规律，建立系统各环节的数学模型[5]。被试件的运动和加载系统的运行，相互影响、相互耦合。系统具有两个输入信号，两个输出信号。系统数学模型如图2所示。

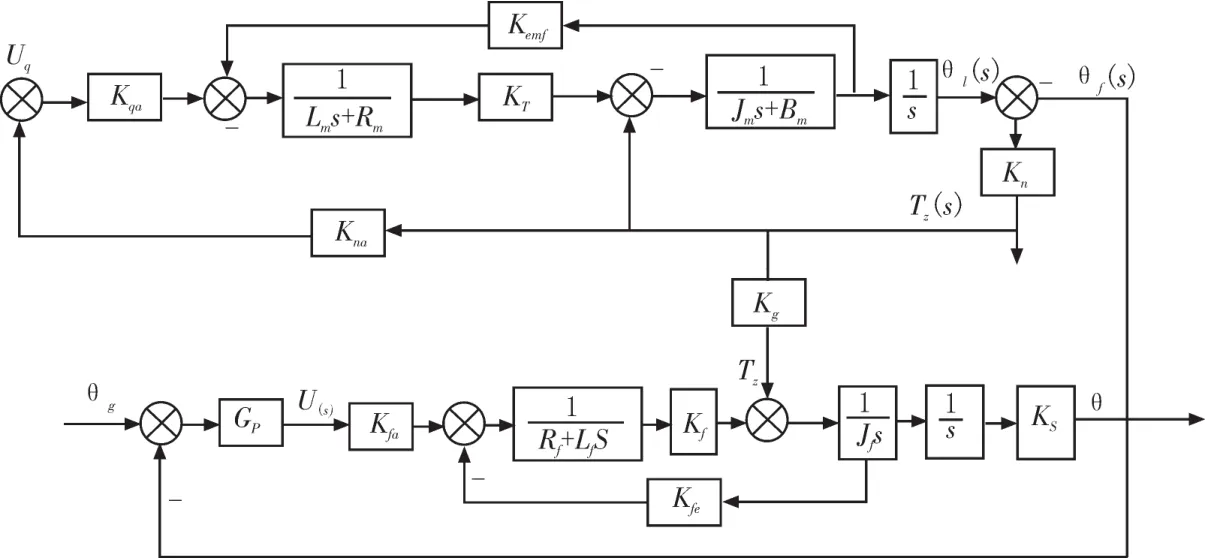
图2 加载系统数学模型

2 多余力及相平面前馈补偿控制算法

2.1 多余力

加载系统中的多余力是指给定力与输出力的偏差，电机加载系统产生多余力的主要因素有：加载电机内部的感生电动势及电磁干扰、加载电机阻尼变化、加载系统机械间隙及连接的刚度、系统惯量、被试舵机运动、系统工作频率等[6]。各因素通过影响加载力或力矩的幅值或相位，产生跟踪误差，即多余力。掌握各因素对多余力的影响特性，改善加载系统的机械连接性能及优化加载部件的参数和选型，可以提高加载系统的性能，但程度有限。根据问题特点，有效的控制策略和有针对性的控制算法是最终的解决办法。本文提出的相平面前馈补偿控制算法较好的解决了非线性时变加载系统的高频段多余力的抑制问题，使得加载系统达到设计要求[7-11]。

2.2 相平面前馈补偿控制算法

前馈补偿控制和反馈控制不同，前馈补偿控制是在明确了可测的已知干扰变量（如：在多余力的分析中，明确多余力与被测舵机的速度有关，且影响较大），控制算法的设计提前考虑到这些因素，通过前向通路，减小干扰信号产生的系统误差[8]。前馈补偿控制对干扰的抑制和控制效果比反馈控制好。但前馈补偿控制往往存在一阶和二阶微分环节，会放大高频干扰信号。因此，能较好的抑制干扰信号，但不能消除，尤其是系统输入频率较高时，系统滞后更严重，抑制能力减弱[12]。

相平面法由庞加莱1885年首先提出，通过图解法求解一阶和二阶线性或非线性系统。相平面上的横坐标为偏差，纵坐标为偏差变化率，相平面上的相轨迹可直观、准确地反映系统的运行特性，如：系统的稳定性，系统的稳态精度，参数变化对系统影响等特性。是推广应用时域分析法的一种图解分析方法。应用相平面法，有针对性的解决系统控制问题，可划分系统的响应的过程，根据不同响应过程的特点，对应到相平面的区域。针对相平面上不同区域的特点，研究给出最优化的控制算法[13]。

进行相平面区域化的分析研究，先分析一下一个阶跃响应，响应曲线如图3所示。

图3 阶跃响应曲线图

我们把上图的阶跃响应曲线分为a、b、c、d 4个循环阶段，各阶段误差e和误差的导数的变化规律相同。a、b、c、d连续循环，稳态误差逐步减小，最终为零。以变量（误差e）和变量（误差的导数）建立相平面坐标。a、b、c、d 4部分分别对应于相平面坐标的4、2、3、1象限。然后进行相平面各区域的特点分析，完成最优PID的设计。

1）加载系统具有时变性和非线性特性，其多余力控制算法由推理原则组R、相平面划区、控制算法组组成。推理原则组R研究各阶段误差e和误差的倒数的变化规律并根据这些规律，确定区块划分组T及各分组的控制方式，形成控制算法组C。如：E1阶段系统误差e大于设定的最大阀值，使控制器输出最大控制量；E2阶段，系统误差e小于设定的最大负向阀值，使控制器输出最小控制量。具体算法规则为：对于推理原则形成的组Ri，符合相平面划区Ti组的条件，就采用控制算法Cj作为PID算法的输出量，其中：i，j=1，2，…，21。

2）相平面划区

相平面划区形成T组，加载系统是一个时变和非线性的系统，系统的载荷谱也是变化的。系统还受系统内各因素的耦合影响、系统外的各干扰因素的影响。这些影响均体现在误差e及其一阶差分Δe上。相平面的不同区域，反映出误差e及其一阶差分Δe的变化特点，表示了系统的不同动态特性。根据这些特点，在相平面上，建立加载系统的特征模式[14]，如图4所示。

图4 相平面分区图

由图4可知，将误差e和一阶差分Δe组成的相平面划分为21个区块，则建立由21个表达式组成的区块划分组。

其中：Δe--e的一阶差分；Δ2e--e的二阶差分。

3）控制算法组

控制算法组定义为C组。研究了阶跃响应曲线，分析了相平面的特点，设计控制算法如下：

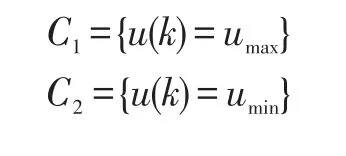
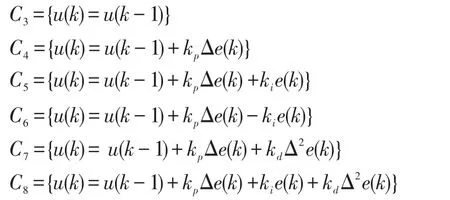
其中：kp,ki,kd分别为比例、积分、微分系数。

3 仿真与分析

3.1 仿真系统的搭建

建立伺服加载系统的数学模型，设计了应用于PID的相平面前馈补偿控制算法，利用matlab中Simulink模块与S函数结合，进行仿真研究。研究多余力的抑制能力，设计更好的用于实际的加载系统和控制算法[15]。仅使用Simulink模块进行系统仿真，如果实际系统及控制算法复杂、逻辑性强，仿真运算会花费大量的时间。两者合理的结合，可以对较复杂的系统进行仿真，效果较好[16-18]。用于仿真研究的复合控制器如图5所示。

3.2 仿真研究结果

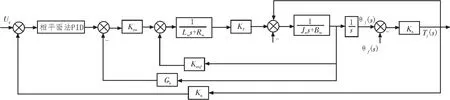
图5 复合控制器

仿真结果发现在频率分别为0.5 Hz、1 Hz采用传统PID控制算法产生的多余力分别为±0.6 Nm、±0.75 Nm，采用相平面前馈补偿控制算法，多余力矩分别为±0.07 Nm、±0.12 Nm。多余力的幅值降低了98.8%、84%。被试舵机端角位置输入为0.5 Hz的正弦信号，采用相平面前馈补偿控制算法，多余力矩输出曲线如图6所示。

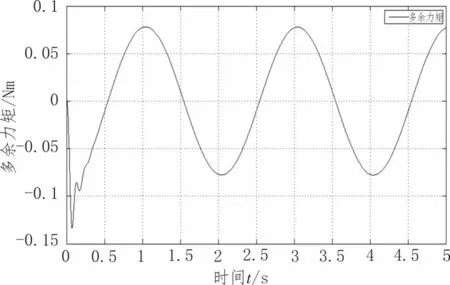
图6 被试舵机输入θg=sin(2πft)，f=0.5 Hz的正弦信号下的多余力矩

4 加载系统实验结果

根据企业技术要求，设计、加工了被试舵机加载试验设备，根据提供的载荷谱进行加载试验验证，结果如下：

采用传统的变参数PID时，系统的跟随曲线明显滞后给定曲线，幅值最大误差为1∘，跟随性很差，说明系统存在非线性的摩擦干扰。在工程中，系统建模时近似处理非线性，还是存在很大误差的。采用相平面前馈补偿控制算法，存在相位和幅值误差，但稳态相位误差可达到工程设计要求。输入信号幅值为20 Nm，稳态幅值误差最大值为0.15 Nm。输入信号幅值为50 Nm，稳态幅值误差最大值为0.17 Nm。实验结果：系统的输出曲线与给定曲线相角滞后很小[19]，幅值最大误差0.2∘，跟踪误差为2%。采用相平面前馈补偿控制算法，给定力矩正弦指令为20sin(ft)Nm、频率均为f=0.5 Hz的加载信号，输出曲线如图7所示。

图7 力矩正弦指令为 20sin(2πft)Nm，f=0.5 Hz实验曲线

5 结 论

多余力的抑制能力是验证加载系统精度的重要指标，通用控制算法针对性不强，对高频段时的多余力的抑制不理想。本论文提出的相平面前馈补偿控制算法[20]，针对加载系统的时变性和非线性的特性，增加了系统在高频段的容错性、适应性和鲁棒性。仿真和试验结果表明该控制算法具有更好的抗扰动性，更能适应系统的参数变化及更高频率的载荷谱跟踪精度[21]。对多余力的抑制能力和力矩跟随特性都优于传统的控制方法。