Robust control for an unmanned helicopter with constrained flapping dynamics

Rong LI,Mou CHEN,Qingxian WU

College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

KEYWORDS Altitude control;Attitude control;Barrier Lyapunov function;Control constraint;Prescribed performance;Unmanned helicopter

Abstract In this paper,a neural network based adaptive prescribed performance control scheme is proposed for the altitude and attitude tracking system of the unmanned helicopter in the presence of state and output constraints.For handling the state constraints,the barrier Lyapunov function and the saturation function are employed.And,the prescribed performance method is used to deal with the flapping angle constraints for the unmanned helicopter.It is proved that the proposed control approach can ensure that all the signals of the resulting closed-loop system are bounded,and the tracking errors are within the prescribed performance bounds for all time.The numerical simulation is given to illustrate the performance of the proposed scheme.

1.Introduction

Recently,unmanned helicopter has been widely used in many applications.With the development of the helicopter,a large number of research results have emerged from the studies of unmanned helicopter control system.1,2In Refs.3,4,a rotation matrix equation was employed in the back stepping procedure,and the nonlinear closed-loop trajectory tracking controller design was presented for the unmanned helicopter system.A model predictive control algorithm was proposed for the linear altitude and attitude unmanned helicopter systems in Ref.5.In Ref.6,the flapping dynamic was considered for the linear unmanned helicopter control system.In Refs.7,8,the sliding mode control method was studied for small unmanned helicopter systems.A disturbance observer based flight control was developed for the unmanned helicopter systems in Ref.9.However,there is few research about the constrained control approach for the unmanned helicopter systems.Thus,in this paper,we will investigate the robust control problem for the altitude and attitude systems in the presence of state and output constraints.

In practical engineering application,there are a lot of the signal constraint problems for practical systems.Usually,according to the signal source,we can classify the constraint problem into three kinds:input constraint problem,10,11state constraint problem,12,13and output constraint problem.14–16Since the output constraint problem was proposed,a lot of new control methods have also been developed.By using command filter,the magnitude constrained adaptive controller design was presented for generic hypersonic aircraft system in Refs.17,18,a fuzzy constrained dynamic output feedback dissipative control was investigated for the time delay systems.In Ref.19,an output constrained control approach was investigated for the non-strict feedback stochastic nonlinear systems.However,the output constraint problem is rarely considered for the unmanned helicopter control systems.To this end,this paper will adopt the prescribed performance method to enhance the output tracking performance of the unmanned helicopter systems.In Ref.20,a barrier Lyapunov function based output tracking controller design approach was proposed for a class of single-input and single-output nonlinear systems.In Ref.15,the barrier Lyapunov function was addressed for the state constrained nonlinear system with unknown control direction.Although there have been some researches about the barrier Lyapunov function method,the state constrained nonlinear control problem should be further developed for unmanned helicopter systems.In this paper,we will present a robust adaptive control algorithm for the state constrained nonlinear unmanned helicopter systems by combining saturation function and barrier Lyapunov function.

As we all know,the model uncertainties of the unmanned helicopter will affect the system tracking performance,and even cause system instability.And neural network method is an effective approach to deal with model uncertainty.21In Ref.22,an adaptive neural network based sliding mode control design strategy was proposed for the air-breathing hypersonic vehicle systems.The neural network based control was investigated for the nonlinear hysteresis systems in Refs.23,24.The neural network was employed to handle robust control and filter problem for the uncertain nonlinear systems with input nonlinearities in Refs.25,26.In Refs.27,28,adaptive control approaches were proposed for the nonlinear stochastic and time-delay systems.In this paper,the uncertainties and constraints will be considered for studying the problem of unmanned helicopter control system with constrained flapping dynamics.

In addition to the uncertainty,there usually exists external disturbance in the nonlinear systems.Disturbance observer is one of the effective methods for dealing with external disturbance.29The extensive application of the disturbance observer was studied for the permanent magnet synchronous motor system in Ref.30.The disturbance observer was employed to design the flight controller of the hypersonic vehicle systems in Refs.31–33.In Ref.34,the authors utilized the disturbance combined model predictive control method,and designed a controller for small-scale helicopter systems.In Refs.35,36,the disturbance observer was combined with fuzzy control approach,and the composed fuzzy controller was designed for a class of nonlinear systems with time-varying disturbance.In this paper,we will use the neural networks and disturbance observer to deal with the uncertainties and external disturbance in the constrained nonlinear unmanned helicopter systems.

Motivated by the previous analysis,we investigate the altitude and attitude tracking controller design for the nonlinear unmanned helicopter systems with state and output constraints.The remainder of this paper is organized as follows.In Section 2,we address the problem statement and preliminaries.The altitude and attitude tracking controller design is presented in Section 3.And the stability analysis is given in Section 4.Thereafter,in Section 5,we present the simulation for the unmanned helicopter systems.Finally,the conclusion is drawn in Section 6.

2.Problem statement and preliminaries

2.1.Unmanned helicopter dynamics

Regarding the fact that forces and moments are mainly contributed by main/tail rotor thrust and torques for the small unmanned helicopter control system,a class of unmanned helicopter flight control systems without cross-coupling term have been established.Interested readers can refer to Refs.7,8for the detailed information of the modeling structure and parameter identification procedure.In this paper,system uncertainty and external disturbance are added,and the unmanned helicopter altitude and attitude dynamics can be described as follows:

where z is the vertical coordinate,v is the vertical velocity,φ,θ,ψ are the Eular angles,and p,q,r are the angular rates.a,b are the flapping angles.Lateral cyclic input δlat,longitudinal cyclic input δlon,main rotor input δcol,and tail rotor input δpedare the control inputs.La,Lbrepresent the control derivative and cross-coupled derivative for roll moment respectively,and Ma,Mbrepresent the control derivative and crosscoupled derivative for pitch moment respectively.Ncol,Npedmean the collective control and pedal control derivatives for yaw moment respectively.Alat,Alonindicate the cross coupled and control derivatives for longitudinal flapping angle,and Blat,Blonindicate the control and cross-coupled derivatives for lateral flapping angle.Zcolis the vertical control gain parameter.g stands for the acceleration of gravity,T means flapping time coefficient,and m is the helicopter mass.Δv,Δp,Δq,Δr,Δa,Δb represent the unknown system uncertainties,and dv,dp,dq,dr,da,dbindicate the external disturbances.Recent researches show that binocular vision can be used to measure the angles of the flapping dynamics.37,38Thus,we assume that the flapping angles a and b are measurable and available in this paper.To achieve the control objective,the following assumptions are required in this study.

Assumption 1.4The ideal trajectory and its higher derivatives are known and continuous.

Assumption 2.9For the nonlinear unmanned helicopter system,the external disturbances dv，dp，dq，dr，da，dband their time derivatives are bounded.

Assumption 3.The flapping angles a,b at initial time are bounded,and they are required to remain in the set:

Assumption 4.2The pitch angle θ and roll angle φ are bounded,and-π/2＜ θ＜ π/2,-π/2＜ φ ＜ π/2.

Remark 1.For tracking control problems,the reference signals are usually preset,so they are possible to know the expected signals and their higher derivatives.In addition,the external disturbances are mainly caused by the changes of forces and torques.Due to inertial action,we can usually consider such disturbances as derivative bounded.Thus,we have Assumptions 1 and 2.

2.2.Saturation nonlinearity

In addition,due to the requirement of state constraints,a control method will be proposed to realize the nonlinear stability control in the existence of state saturation nonlinearity.Considering the characteristics of saturation nonlinearity,the saturation operation can be defined as10

where xsi∈ R,and sat（·）represents the saturation operation.xiumaxand-xiumaxare the upper and lower saturation bounds of xsi,respectively.To efficiently tackle the saturation problem,it can be approximated by the following smooth function25:

where Tr（·）indicates the custom hyperbolic tangent function,which can be shown in Fig.1.

2.3.Barrier Lyapunov function

For stability analysis of nonlinear constrained system,we give two lemmas:

Fig.1 Hyperbolic tangent function.

Lemma 1.For|X|＜k,X∈R and k＞0,the barrier Lyapunov function satisfies the following inequality15:

Lemma 2.Consider a class of nonlinear systems as20

where X= ［χT，xT］Tis the state vector,and f（·）denotes the continuous function vector.For any positive constants ki,i=1，2，...，n,define the open set as Z:= ｛χ ∈ Rn:|χi|＜ki，i=1，2，...，n｝ ⊂ Rn.Suppose that there is a positive definite function V:E → R+satisfying V（ χ）→ ∞,as ‖χ‖ → k,γ1（‖x‖）≤ U（ x）≤ γ2（‖x‖）,where γ1and γ2are the class K∞functions.Let Π:=V+U,and for the positive constantsif the following inequality holds:

then we can conclude that χ will be bounded and the bounded set is χ∈Z.

2.4.Neural network

As we all know,the neural network can effectively tackle uncertainty,and the neural network approximator has a concise structure.For linear parameterized RBFNN,the expression can be expressed in the form of26

where Z∈Rnis the input of NN,S indicates the basis function,means the update law of NN,ε is the estimate error,andrepresents the unknown nonlinear function.Based on the description of NN,the optimal weight value of NN can be achieved as

where ε*is the optimal approximation error.And it satisfiesrepresents the upper bound of approximation error.

3.Robust flight control design

For this part,we will give a specific adaptive controller design procedure,which involves neural network approximator and disturbance observer.The whole design procedure can be divided into the following three parts.

3.1.Altitude-attitude loop

For achieving the control design procedure,define the tracking errors as follows:

where zd,φd,θd,ψdindicate the ideal trajectories of height,roll angle,pitch angle and raw angle,respectively.Define the performance function as

where ρi∈ R represents the positive decreasing function.For Eq.(12),l＞0 decides the convergence rate of tracking error,and ρi0＞ 0,ρi∞＞ 0 decide the bounds of the tracking errors.The error transformation function is defined as

Additionally,the time derivative of ϖican be rewritten in the form of

Substituting Eqs.(16)and(17)into Eq.(15),then we have

In order to conveniently discuss the problem of error transformation dynamics,we define the matrix M1∈ R4×4and vector N1∈R4in the form of

According to Eqs.(1)and(18),we have

The virtual control law is designed as follows:

whereKA=＞ 0，KA∈ R4×4is the designed matrix.Invoking Eqs.(21)and(22),we have

Meanwhile,we have the following matrix transposition,which will be used for the controller design in the next step.

3.2.Linear and angular velocity loop

The tracking errors are defined as

where vd,pd,qd,rdindicate the ideal control laws,which have been given in Eq.(22).Invoking Eqs.(1)and(25),the time derivatives can be obtained as

Considering the state constrains,we construct the virtual control law as

where lpq＞0 and lVr＞0 are design constants.Substituting Eq.(28)into Eq.(1)yields

where KVr=is the estimate ofand^δvand^δrare the disturbance estimate value.Additionally,the ideal virtual control law is given by

where Kpq=is the estimate ofand^δvand^δrare the disturbance estimate value.The neural weights are updated by

3.3.Rotor dynamic loop

Define the tracking errors as

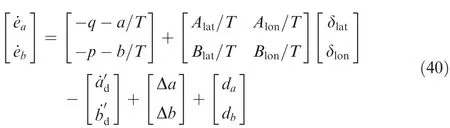
Since Δa and Δb are unknown,using the RBFNNs to approximate labΔa and labΔb,we obtain

where lab＞0 represents the design parameter,is the ideal neural network weight,and εabis the optimal estimate error.Substituting Eq.(41)into Eq.(40)yields

To eliminate the effects of state constraints,the barrier Lyapunov function method was employed,and the error bounds are chosen as αb＞ 0 and βb＞ 0.And the ideal tracking performance requires the flapping angle tracking error constrains restricted to the set of ea＜ αb,eb＜ βb.The control law can be designed in the form of

where Λab= ΛTab＞ 0,and σab＞ 0 are the design parameters.and we have‖˙δab‖≤Υab,where Υabis a constant.It is not difficult to find out by Eq.(42)that there exist uncertainties and external disturbance.The neural network has been taken to deal with uncertainties,and for counteracting the effects of external disturbance δab,the disturbance observer will be employed.And then,the disturbance observer can be designed as follows:

4.Stability analysis

We select a Lyapunov function of altitude-attitude loop in the form of

According to Eq.(23),the time derivative of VYcan be written as

Consider the Lyapunov function candidate of linear and angular velocity loop as

According to Eqs.(37)and(38),the time derivative of VAcan be derived in the form of

Substituting Eqs.(33)and(34)into Eq.(50),we have

Invoking Eqs.(35)and(36),the time derivative of VAcan be rewritten as

According to Eq.(1),we have

For achieving flapping angle constrained controller design,the barrier Lyapunov function is employed in the controller design procedure.Choose the Lyapunuv function candidate of rotor dynamic loop as

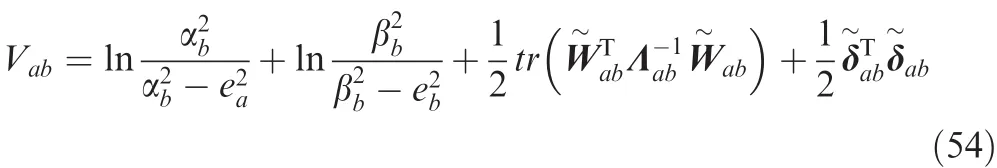
Invoking Eq.(42),the time derivative of Lyapunov function candidate can be derived as

Substituting Eq.(44)into Eq.(55),we obtain

According to Eq.(45),the time derivative of Vabyields

On the basis of Eq.(45),we can conclude that

In summary,we conclude the following theorem,which includes the adaptive control procedure in the presence of neural networks and disturbance observers.Eventually,the design requirements are given to guarantee the stability of the unmanned helicopter system.

Theorem 1.For the uncertain unmanned helicopter altitude and attitude system dynamics described by Eq.(1)with boundary conditions,if there are parameters μVr＞ 0,μpq＞ 0,μab＞ 0,the following inequalities hold:

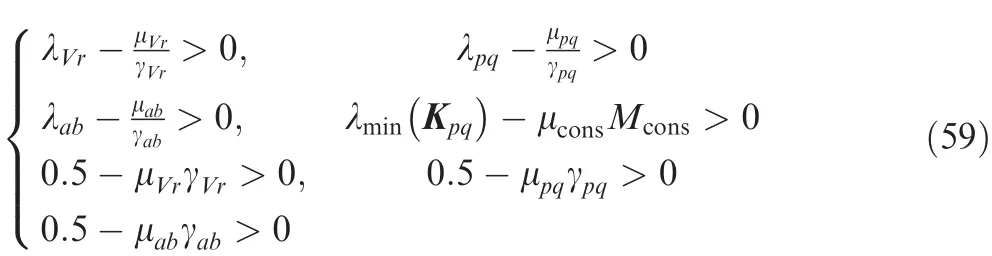
we can conclude that the bounded stability of closed-loop system is guaranteed under Assumptions 1–3,the proposed control Eqs.(22),(31),(32)and(43),the adaption laws Eqs.(33),(34)and(44),and the disturbance observers Eqs.(35),(36)and(45).Furthermore,the flapping angle constraints are never violated,i.e.,∀t＞ 0,|a（ t）|≤ a-+αb,|b（ t）|≤ b-+βb.

Proof.On the basis of the proposed Lyapunov function candidates Eqs.(47),(49)and(54),we define

Invoking Eqs.(48),(53)and(58),we obtain

Considering the Young’s inequality,we have the following facts:

And according to Assumption 2,we know that the time derivatives of external disturbance are bounded.Then we obtain

Considering Eqs.(62)–(65),it can be obtained as follows:

where γVr,γpq,γabare constants.Define the variable

Table1 Parameters of unmanned helicopter dynamics.

Fig.2 Response of attitude angles.

Fig.3 Response of vertical height z.

Fig.4 Response of attitude angle velocities.

Fig.5 Response of vertical linear velocity v.

Fig.6 Response of flapping angles.

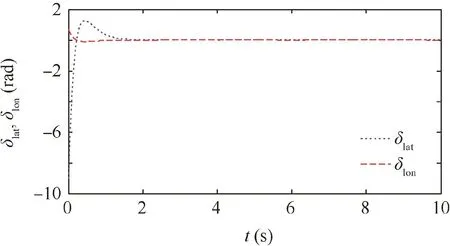
Fig.7 Control inputs δlatand δlon.

Fig.8 Control inputs δcoland δped.

According to Lemma 1,we have

According to Lemma 2 and Eq.(59),we can conclude that the closed-loop system is stable,and the flapping angle constraints are never violated.

Remark 2.Firstly,we should ensure that the design parameters satisfy the inequalities in Eq.(59).In the developed constrained controller,the design parameters KA，KVr，

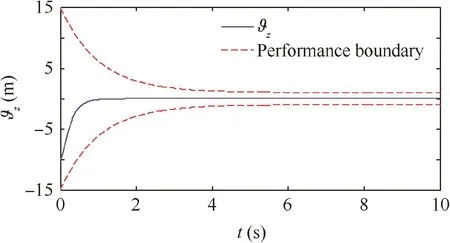
Fig.9 Height tracking error ϑz.

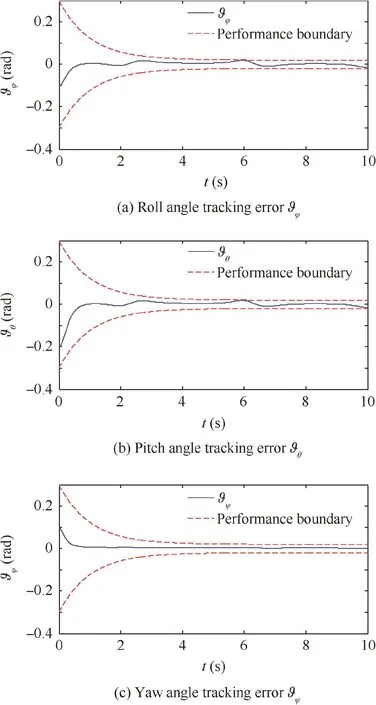
Fig.10 Response of angle tracking errors.

Kpq，ka，kb，ΓVr，Γpq，Γabneed to be tuned to obtain good transient performance and closed-loop stable performance.If the tracking error is desired to be lower,we should increase the controller gains KA，KVr，Kpq，ka，kb.And decreasing the neural network update gains ΓVr，Γpq，Γabcan improve the tracking performance.In addition,the appropriate choice of neural parameter can accelerate the convergence rate of the system.

5.Simulation study

In this section,numerical simulation of the unmanned helicopter system is conduced to verify the validity of the proposed prescribed performance controller design.Specifically,the parameters of unmanned helicopter dynamics Eq.(1)are listed in Table 1.7

In this section,we investigate the control tracking performance of the unmanned helicopter system.Since Assumption 1 requires that the tracking signals be smooth enough,the filter link is added on the basis of the square wave signal.The simulation time is set 10 seconds,and the reference tracking signals are defined as zd（t）=10 m, φd（t）=squφ·filter rad, θd（t）=squθ·filter rad,ψd（t）=0 rad.squφ,squθindicate the square wave signals with value of 0.2 rad and period of 4 s.The initial height and attitude angle are z（ 0）=0 m, φ（ 0）=0.1 rad,θ（ 0）=0 rad, ψ（ 0）=0.1 rad.The parameters of controllers and neural network adaptive laws are chosen as follows:βb=0.2.Meanwhile,the prescribed performance parameters can be chosen as ρ0=［15，15，15，15］T,ρ∞=［1，1，1，1］T,l=1.

Fig.11 Response of attitude angles.

Under the proposed robust adaptive tracking control scheme,the simulation results are shown in Figs.2–10.And the corresponding control thrust and control moments are given in Figs.7 and 8.The response curves of attitude angles are showed in Fig.2.The response curves of attitude angular rates are presented in Fig.4.Fig.3 shows the response curves of altitude,and Fig.5 shows the response curves of altitude velocity.Fig.6 shows the response curves of flapping angles.Figs.9 and 10 give the output tracking errors and their boundaries.

Fig.12 Response of angle velocities.

Fig.13 Response of vertical height z.

Fig.6 shows that the flapping angles satisfy the ideal saturation conditions.From Fig.10,we note that the tracking performance is satisfactory and the tracking errors quickly converge to zero for the uncertainty in the presence of the uncertain dynamics.According to the definition of prescribed performance function,the performance boundaries are plotted in Fig.10.It can be seen that there exists steady error,which is inevitable for the ideal output trajectory due to existence of state saturation.

Based on the above simulation results and analysis,the proposed robust adaptive tracking control approach is valid for the uncertain MIMO nonlinear systems with uncertainties,disturbance and state constraints.

In addition,we will give the general back stepping control simulation in the following.The response curves of attitude angles are showed in Fig.11.The response curves of attitude angular rates are presented in Fig.12.Fig.13 shows the response curves of altitude,and Fig.14 shows the response curves of altitude velocity.Fig.15 shows the response curves of flapping angles.

Fig.14 Response of vertical linear velocity v.

Fig.15 Response of flapping angle b.

Compared to the simulation results in Figs.11–15,it can be shown that the flapping angle can easily violate the state constrains.By employing the compared simulation results,we can conclude that the proposed control method can not only deal with the uncertainties and disturbance,but also ensure the prescribed boundaries for state and output signals.

6.Conclusions

In this paper,we address the adaptive prescribed performance based robust neural control approach for the unmanned helicopter altitude and attitude tracking systems with constraints.For the proposed algorithm,the flapping dynamics with constraint are considered.Finally,the stability analysis and simulation show that the proposed approach is effective.

Acknowledgements

This study was supported by the National Natural Science Foundation of China(Nos.61573184,61751210),Aeronautical Science Foundation of China(No.20165752049),and the Fundamental Research Funds for the Central Universities of China(No.NE2016101).