杜仲短周期矮林地上部分生物量模型

马顺兴, 丁欢欢, 刘慧东, 朱景乐, 殷世雨, 张学献, 杨书涛, 孙志强

(1.河南内黄林场，河南 安阳 456300; 2.国家林业局泡桐研究开发中心，河南 郑州 450003; 3.信阳市南湾实验林场，河南 信阳 464031; 4.栾川县林业局，河南 洛阳 471500)

高密度短周期矮林种植模式可在短期内大量供应生物质，以及为医药及其他工业领域提供原材料[1-4].传统上，人们多采用树高、胸径与生物量的相关性特异方程对杜仲生物量进行估测[5-7].譬如，彭华昌[8]测量了4年生杜仲人工林的单株生物量，简单拟合地上和地下部分总生物量的回归方程；周政贤等[9]分别针对杜仲乔木林的干材、树皮、叶片等建立了各器官的生物量方程.罗伟祥等[10]针对7 a杜仲人工林同样是以D2H为自变量建立了生物量的回归方程.关于杜仲果园化栽培的研究，主要涉及不同功能部位的产量及幼龄生物量等[11-12].吴敏等[11]对雄花、果实和叶片产量开展了调查.杜笑林等[12]对果园化栽培建园前4 a生物量进行了报道.涉及杜仲短周期矮林(亦被称为叶用林)生物量的研究不多[13-15]，关于生物量方程的拟合鲜见报道.对于短周期矮林，特异性方程的使用需适合矮林所具有的高密度或多茎的特征[16,17].这种特异方程应满足对单株植物生物量的精确估计和总生物量的可靠采样和计算方法[24].本研究以密度为6.7株·m-2的杜仲短周期矮林为研究对象，初步拟合了第二轮伐期杜仲重要特征指标与地上部分生物量的估算方程，为低密度下多茎生长条件下的生物量估测提供依据.

1 材料与方法

1.1 试验地概况

试验地位于中国林业科学研究院经济林研究开发中心孟州基地(112°42′58″E,34°51′38″N).该基地南临黄河，属黄河滩地，大陆性暖温带季风型气候，年降水量约549.9 mm，年平均气温14.3 ℃，无霜期224 d.具有中部平原地区黄河古道沙地典型的立地特征.沙壤土，土壤0～40 cm处的理化性质为：pH=8.67，有机质含量4.07 g·kg-1，总氮含量0.03 g·kg-1，有效氮含量18.79 mg·kg-1，有效磷含量4.80 mg·kg-1，有效钾含量156.62 mg·kg-1.

1.2 试验设计

杜仲矮林于2015年3月营造，采用宽窄行栽植模式，宽行距1 m，窄行距0.5 m，窄行内株距分别为0.2 m，密度6.7株·m-2.于2015年10月收获平茬，2016年春季在杜仲生长初期进行抹芽，每株留一个主芽.适时浇水、除草，试验期间不施肥.

1.3 生长指标和生物量的测定

2016年10月9日剪取333株，地上部分留5 cm，分别用卷尺和游标卡尺测量植株的茎长(cm)和基径(mm)；随机选取茎干中间三分之一部分的4片叶，称量其鲜重，记为W4，并称量4片叶在内的所有叶片的鲜重，记为W；剪取每株苗木中间20 cm的茎干，剥皮后分别称皮和杆的鲜重.将采集的叶片、树皮和枝干带回室内于65 ℃烘干后再分别称重(4片叶干重记为W1；20 cm皮干重记为W2；20 cm杆干重记为W3).

单株叶干重(g)=(W1/W4)×W

(1)

单株皮干重(g)=(W2/20)×茎长

(2)

单株杆干重(g)=(W3/20)×茎长

(3)

1.4 数据处理及统计分析

1.4.1 模型自变量的选择 选择与生物量相关性较高的自变量基径(D)和茎长(L)易测因子及其组合DL、D2L、D3来拟合生物量模型，以提高模型精度.通过相关性分析确定各器官生物量模型拟合的自变量.样本的调查数据分为两部分，一部分用于模拟模型，另一部分用于检测模型的拟合精度.

1.4.2 模型的选取 选用以下5种模型进行生物量模型拟合:

Y=a+bX

(4)

Y=a+bX+cX2

(5)

Y=a+blnXv

(6)

Y=aXb

(7)

Y=a×ebx

(8)

式中:Y为生物量；X为自变量；a为回归常数；b、c为回归系数.

1.4.3 模型的拟合与及检验 采用双变量Person双尾检验(P<0.05)检验植株参试指标，以及指标及其组合与各部位生物量的相关性；采用SPSS 20.0软件对数据进行回归分析，拟合模型.用判定系数(R2)、估计值的标准误(SEE)、标准化残差分布，并通过对模型相关参数的筛选比较模型总相对误差(RS)和平均相对误差绝对值(RMA)，以评价模型优劣；选择模型显著(P<0.05)、相关性最密切、拟合度最好的生物量回归模型作为最佳估算模型[16-19].

2 结果与分析

2.1 参试指标范围

样本的调查数据共两部分，一部分是模拟模型，采集263个样本；另一部分是检测模型的拟合精度，采集50个样本.具体的调查结果见表1.其中用于精度检测的样本各指标均在模型拟合各指标的分布范围内，可用来检测模型拟合的精度.

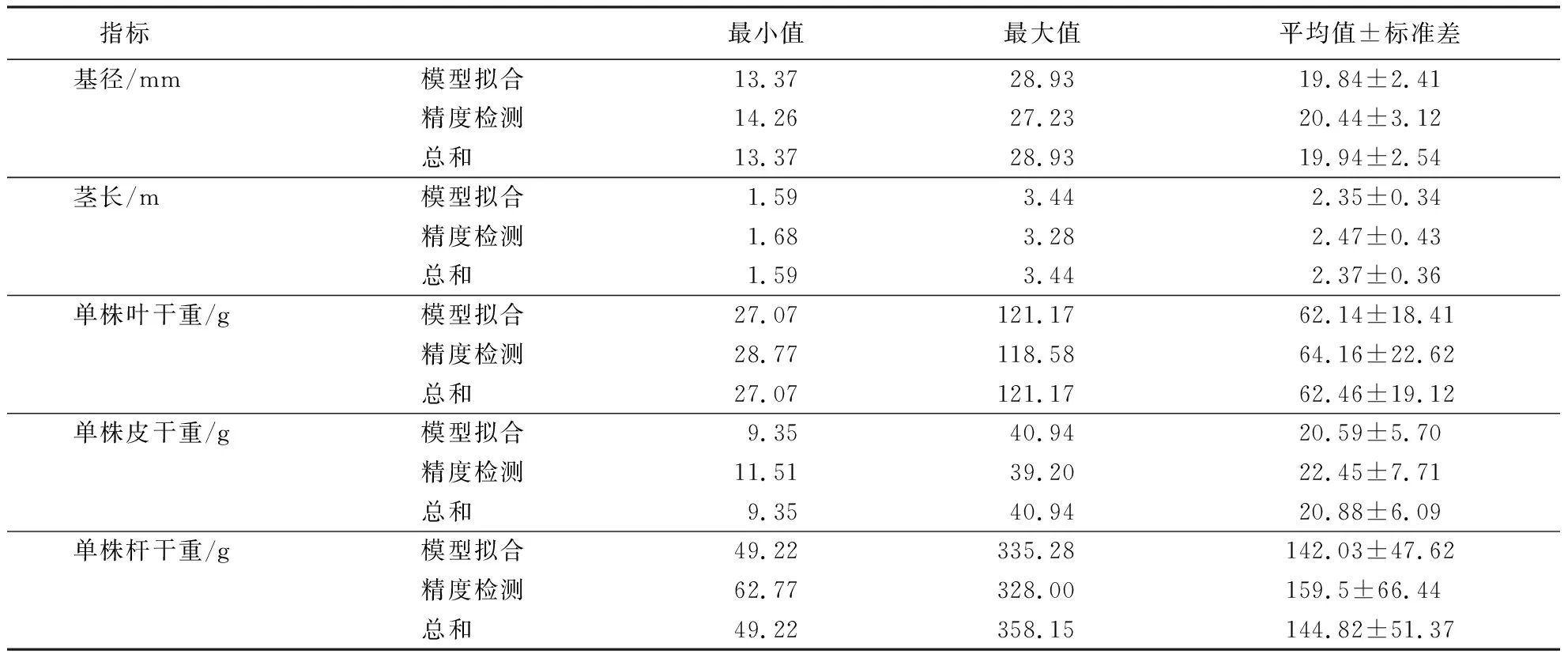
表1 参试样本的各指标分布范围Table 1 Parameter ranges for different parts of samples

2.2 参试指标及其组合与单株叶、皮、杆干物质的相关性

杜仲单株叶干重、皮干重和杆干重均与基径和茎长呈极显著的正相关关系(R2为0.722～0.867，P<0.000)(表2)，同时也与基径×茎长、基径2×茎长、基径3呈极显著正相关(R2>0.729,P<0.000)，其中均以基径×茎长与单株叶干重、单株皮干重和单株杆干重的相关性最强，相关系数分别为0.812、0.927、0.920.因此，本研究以基径×茎长为自变量拟合单株各部位干重的模型.

表2 单株叶干重、皮干重和杆干重与各指标及其组合的相关性1)Table 2 Correlation between above-ground biomass per plant and growth indexes

1)***表示差异达到P<0.001显著水平.

2.3 单株各部位干重模型的拟合

选取5种常用的生长特异性模型类型进行杜仲单株叶、皮、杆干重的回归分析.各部位干重的模型类型及其参数如表3所示.由表3的结果可知，单株叶干重、单株皮干重和单株杆干重的回归模型拟合效果极显著(F检验，P<0.001)，除单株叶干重的回归系数R2偏小(为0.626～0.662)外，单株皮干重和单株杆干重的回归系数均大于0.818.单株叶干重和单株杆干重模型均是幂函数模型(R2最大)，拟合效果最好.模型式分别为：Y=1.131(DL)1.040，Y=0.805(DL)1.340，回归系数分别为0.662、0.852.而单株皮干重则以二次项的模型拟合效果最好，模型式为：Y=0.068+0.387(DL)+0.001(DL)2，相关系数为0.857.

2.4 模型残差分析

采用单株各器官生物量模型标准化残差对模型进行诊断分析，结果表明，叶、皮、杆生物量的模型标准化残差频率直方分布图呈正态分布，且在横坐标方向上呈现随机分布状态，而标准化残差绝对值均未超过默认值(3).表明本研究所选的估算模型比较合理.

2.5 模型精度的检验

单株各器官及个体生物量估算模型的RS和RMA值均在精度允许范围内(表4).单株叶、皮、杆生物量估算模型的RS值均小于10%，其值分别为-14.80%～1.62%、-2.18%～1.39%、-4.84%～2.83%，绝对值最小所对应的模型分别是二次函数模型、幂函数模型、二次函数模型.单株叶、皮、杆生物量估算模型RMA值均显著高于RS值，其值分别为15.67%～18.50%、10.08%～12.52%、11.42%～16.14%，最小值所对应的模型分别是线性函数模型、幂函数/二次函数模型、幂函数/二次函数模型.整体上，模型估测效果较好，可以进行生物量估测.

表3 杜仲单株叶、皮和杆干重的模型Table 3 Equation indexes for leaf, bark, stalk biomass per plant

3 讨论

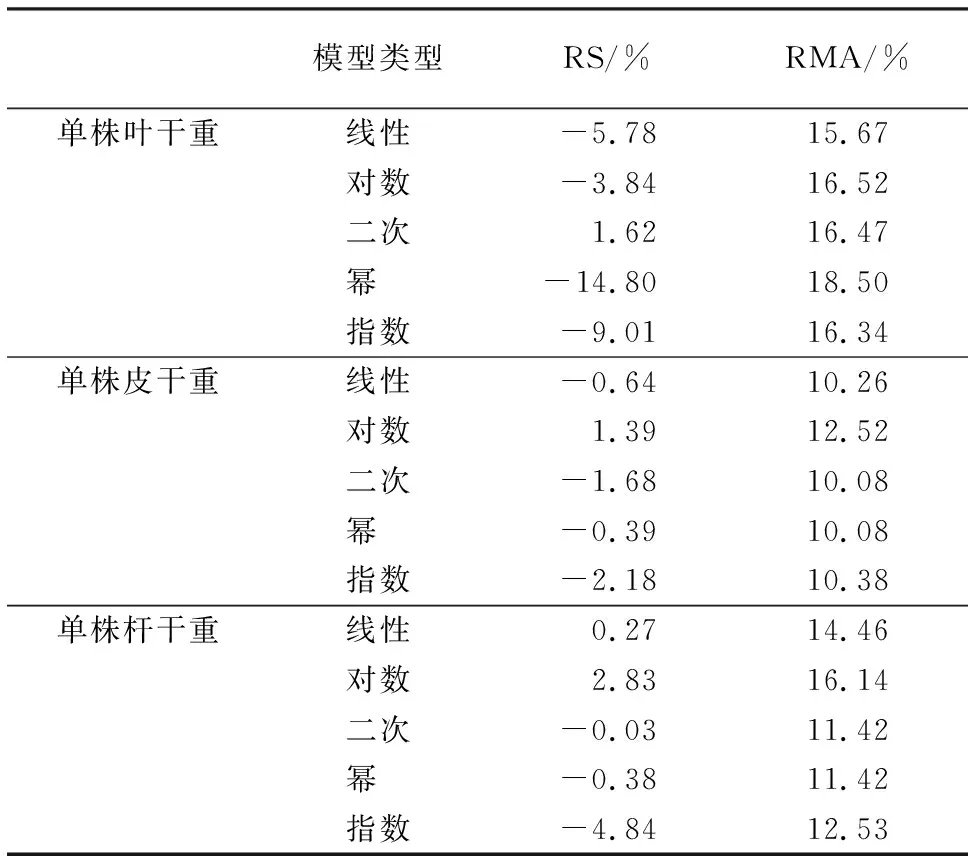
表4 回归模型精度检验Table 4 Accuracy assessment of the equations

本研究通过分析易测因子基径D(mm)、茎长L(m)及其组合DL、D2L、D3与各部位干重的相关关系，选取相关性最强的指标作为自变量.分析模型的标准化残差可以检验回归方程的方差齐性和检测异常值[20].本研究结果中模型的残差是任意分布的，呈现正态分布的特点，达到了一定的精度要求.RS反映回归模型系统偏差的情况，RMA反映各器官及个体的平均相对误差，二者均在不同程度上反映了回归模型的拟合程度[16].本研究采用未参与建模的50个样本的总相对误差(<30%)和平均相对误差绝对值(<20%)进行模型精度验证[21]，结果表明误差在精度要求范围内.

本研究拟合出了叶、皮、杆3个部位的单株生物量模型，实现了在不破坏植被前提下估测植物园生物量的目标.模型估测具有简便性和实用性的优点，且可减少对植被的破坏[22,23]，但有一定的局限性，要求样本的密度在6.7株·m-2左右，且1.59 m<茎长<3.44 m，13.37 mm<基径<28.93 mm.杜仲矮林的栽培目标是高效集成生产叶和皮，每年9—10月轮伐一次，第3年开始低密度下根桩可保留3～5个主茎.

植株的生长状况会因立地条件和气候的不同而存在一定差异，在研究区之外应用本研究建立的回归估测模型时，需用拟合率检验并确定校正值，当拟合率大于70%时，则可认为该模型适合于该地区[17].本研究在控制单株茎干数的前提下，以单株为研究单位拟合了生物量的方程，对于模型中自变量超过该研究范围，进行直径、植株高度等变量外推时需要做进一步验证.

本研究结果表明，单株叶干重、皮干重和杆干重的最优模型拟合的方程式分别为Y=2.618+1.097(DL)+0.003(DL)2、Y=0.068+0.387(DL)+0.001(DL)2、Y=25.545+3.042(DL)+0.010(DL)2/Y=0.690(DL)1.377.在模型评价指标的选取上，不仅采用常规的判定系数和参数估计值的标准误，还采用了残差分析来综合评价模型的拟合效果，能较全面地反映模型的优劣.