城市排水管中过流断面平均流速计算方法研究

杨志超，刘 佳

（1.北京建筑大学，北京 100044；2.北京市理化分析测试中心，北京 100089）

0 引言

城市的排水管道系统是现代化城市不可或缺的重要市政基础设施。其主要作用是收集、输送城市降水和生活污水，提供人们一个安全舒适的生产、生活环境。但随着近年极端天气频发[1]、城市化的加速扩张和人们对高质量生活的追求，城市排水管网承受着巨大的运行压力。遭遇极端天气，管网排水不畅不但会造成道路大面积积水，还会污染自然径流。研究显示，一些发达国家的暴雨事件中自然水体高达80%的污染负荷来源于管道沉积物[2]。流速作为研究排水管网输送能力、沉积物冲刷、污染物扩散等问题的基础数据，其计算方法对边界条件的要求、计算难度、准确度等都直接影响最终结果。

1 水力计算的发展

19世界末到20世纪中叶，单位线法、曼宁公式、圣维南方程组等经典方法的提出，为排水动力模型的发展奠定了基础。20世纪70年代，计算机技术被引入到排水管网的计算中，迎来了计算能力的爆发式增长。从早期的斯坦福模型（Stanford Watershed Model，SWM）、暴雨洪水管理模型（Storm water management model，SWMM）等，到水文计算模型（HSP）、伊利诺雨水管道系统模拟模型(ISS)等进一步促进了排水系统设计、规划和管理的进步与发展[3]。

随着我国水力学和计算模拟的稳步发展，相继诞生了许多类似的管道计算模型，其中以城市雨水管道计算模型（SSCM）和数字排水平台（DigitalWater+DS）最为突出。这些具有我国自主知识产权的排水模型出现，将帮助中国城市更好的完成排水管网的设计规划和雨洪管理。

2 断面平均流速的计算方法

在计算排水管内断面平均流速时一般使用三种方法：工程手册公式、数学计算公式、计算机模型模拟。工程手册内的公式，为追求计算简便概化了一些边界条件因素。而计算机模拟则是在数学计算基础上形成的综合运用，边界条件更加细化，分析的结果更为精准、多样。

2.1 恒定流条件下的排水管水力计算

在一般工程设计时，通常假定排水管内流体为恒定流以减少计算量。GB50014-2006（2014年版）《室外排水设计规范》中规定了明渠恒定流流速公式[5]，如公式（1）。

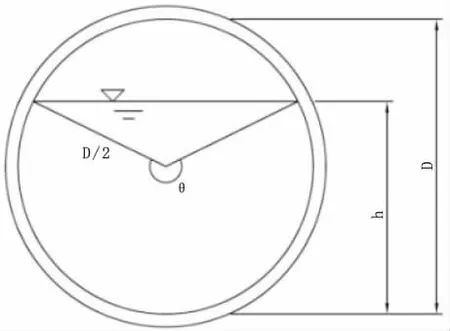
图1 管道断面示意图

式中：v为截面平均流速，m/s；n为管道内壁摩擦系数；R为水力半径；I为水力坡度。

2.2 圣维南方程组

建立一维圣维南方程组，一直是求解管道流体的经典方法[5]。式中：B为当量宽度；Z为水位；Q为断面流量；q为旁侧流入流系数；a为动量校正系数；u为过流断面平均流速；A为过流断面面积；h为水深；S0为河底比降；Sf为摩阻比降。

当不考虑旁侧流入的情况下q=0，且取校正系数a=1。

Preissmann窄缝宽度法在求解时，运用四点加权隐式格式对方程组进行离散，既具有较好的数值稳定性、鲁棒性，又提供了较高的计算效率。这种方法提供三种已知边界条件求解形式：①水位边界条件的计算；②流量边界条件的计算；③水位、流量关系边界的计算[5]。

2.3 FLUENT模型模拟

FLUENT具有基于有限体积法的求解器，利用偏微分方程组离散化为代数方程组，然后用数值方法求解代数方程组以获取流场解。由于采用了多种求解方法和多重网络加速收敛技术，使其达到最佳的收敛速度和求解精度。

图2 FLUENT模型模拟过程

2.4 三种流速计算方式的比较

对工程手册公式、圣维南方程组、FLUENT模型模拟三种不同计算方法用于排水管道流速计算进行比较见表1。

表1 三种流速计算方式的优劣对比

3 三种流速计算方法的结果比较

假设一个直径为1 m的水泥圆管，粗糙系数为n=0.012，管道长度L=500 m，坡度为0.0006。其中流体为恒定流时水深为0.5 m，由手册公式计算出恒定流流量Q=0.318 m3/s，断面平均流速v=0.810 m/s。

当管道内流体呈现非恒定流状态，使用圣维南方程组求解管道内各点的断面平均流速状况。假设排水管道未有支流汇入，管内流体流量为Q=0.318 m3/s，测量上游水深为0.4 m时，经由圣维南方程组和FLUENT计算后管道中各点平均流速的变化如表2及图3。

表2 上游水深为0.4m时分别使用圣维南方程组和FLUENT求解流体流速

图3 上游水深0.4m时管道水平均流速变化

4 结论

在计算管道内流体流速时，计算精度要求和能提供的边界条件值，是选择对应计算方式的前提。对同一管道条件进行计算时，三种方法分别具有不同适用条件和计算特点。根据不同的使用需求和对结果的精度要求，选取不同的计算方法能显著提高工作效率。本文对这三种计算方法的适用性分析如下：

（1）工程手册公式：适用于恒定流状态，对已知流体边界条件要求较少，不过由于无法计算非恒定流，距离实际状态较远。该方法可适用于管道设计、宏观管网的预测和对流速计算精度要求不高的案例。

（2）数学模型计算：以圣维南方程组为例，该方程组可适用于非满管流、明满过渡流和满管流三种不同情况，但如果需要计算管内某点过流断面平均流速，不仅需要给出相应的边界条件，而且需要自己设计、编写计算程序，需要用到大量计算，通用性不高，可视化能力不强。可适用于对多种管道特征条件下平均流速的计算，由于公式的限制仅限于对水深、流量等变化量进行求解。

（3）计算机模拟：利用已经编写完成的一套综合性数学模型来分析计算，通用性和可视化能力很高。但如果对象为非满管流，FLUENT很难对两相流模型进行空间比例划分，而是以混合的状态共同进入管道。所以一般采用人为的方式，将水-空气临界面做成固定边界进行分析。也导致了如果计算多个水深的非满管流流速，需要进行大量的模型构建工作。在分析管长-直径比例过大的模型时，有限元化分和分析计算需要耗费大量时间。由于使用了一整套综合的数学模型，FLUENT模型模拟除了能给出管道流量、流速的结果，还能计算出管道各点位相应剪切力、压力、温度变化等等相关数据。所以计算机模型更适合对某种单一条件下，管内各点的综合情况分析。