峡门河水文预报方案建立与修正
2018-12-14郝强
郝 强
(甘肃省武威水文水资源勘测局,甘肃 武威 733000)
水文预报是现代水文学科的分支,是建立在充分掌握客观水文规律的基础上,预报未来水文现象的一门应用科学技术[1]。目前,许多流域水文测验设施的密度,无法满足建立高精度的水文预报方案,而水文要素作为典型的时间序列要素,具备时间序列统计分析的可行性[2],鉴于此,基于统计学方法的长期预报在小流域水文预报探索阶段有无可比拟的优势。
作为区域经济支撑点哈溪镇的过境河流,峡门河长期缺乏必要预报手段,不利于抗旱防洪,开展相关研究势在必行。本文将以峡门河33年实测数据为支撑,探索符合实际、具备一定精度的长期预报方案,并尝试对2018年水情进行预报。
1 流域概况
峡门河又称黄花滩河,属石羊河二级支流,发源于祁连山北麓甘肃天祝县与青海门源县交界处的青分岭、红腰岘以东,沿东偏北向至天祝县哈溪镇与哈溪河汇合成黄羊河,全长34 km,流域面积325 km2,多年平均降水量489 mm,多年平均径流量0.847亿m3。从1989年至2008年,总体上天然来水量为减少趋势,年际变幅大。最小年径流量0.5798亿m3发生在2013年,最大年径流量1.482亿m3发生在1993年。径流年内分配极不均衡,4月~10月径流量占总量87%以上,11月至次年3月径流量不到总量14%,一般最小径流出现在2月份。
2 研究方法
2.1 周期均值迭加法
将水文要素的时间变化过程概化为多个周期序列的迭加,通过F检验判定有k个显著周期,则其数学形式表示为:
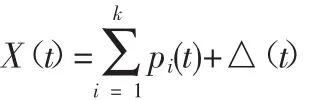
其中X(t)为t时刻水文要素,pi(t)为t时刻的第i周期,△(t)为 t时刻误差[3]。
如果判定存在若干显著周期,通过顺序周期迭加就可以实现预报。
2.2 ARIMA模型法
ARIMA模型(Autoregressive Integrated Moving Average Model),全称为自回归积分滑动平均模型,是指将预测对象的时间变化过程视为一个随机序列,用一定的数学模型来近似描述,从而将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型[4]、[5]。数学模型确定后就可以通过时间序列的实际值来预测未来值。
借助SPSS的时序分析模块可以实现ARIMA模型预报。
3 预报演算
使用峡门台水文站(1985年~2007年)与哈溪水文站(2008年~2017年)实测数据,进行周期均值迭加演算与ARIMA模型演算,确定参数值。
3.1 周期均值迭加演算
在数据文件yubaodata1.xls中新建工作表,复制实测数据,保存文件。
打开周期均值迭加程序,选择预报站点为哈溪,预报时段为年径流,校核资料个数5,预报数值1,依次点击输入资料、计算、显示预报结果、显示预报图形,即可得到预报结果,如图1。
图1 预报结果
3.2 ARIMA模型演算
打开SPSS数据编辑器导入数据,修改变量名称,输入预报年份。
点击分析→预测→创建模型,打开时间序列建模器,自变量“年份”,因变量“年径流量”,方法选择“ARIMA”,选择模型参数,如图2。
图2 选择模型参数
分别选择模型参数(p,d,q)为(1,1,1)、(1,1,2)、(1,1,3)、(1,1,4),点击继续,开始预报调试。
四种参数条件下的演算结果如表1。
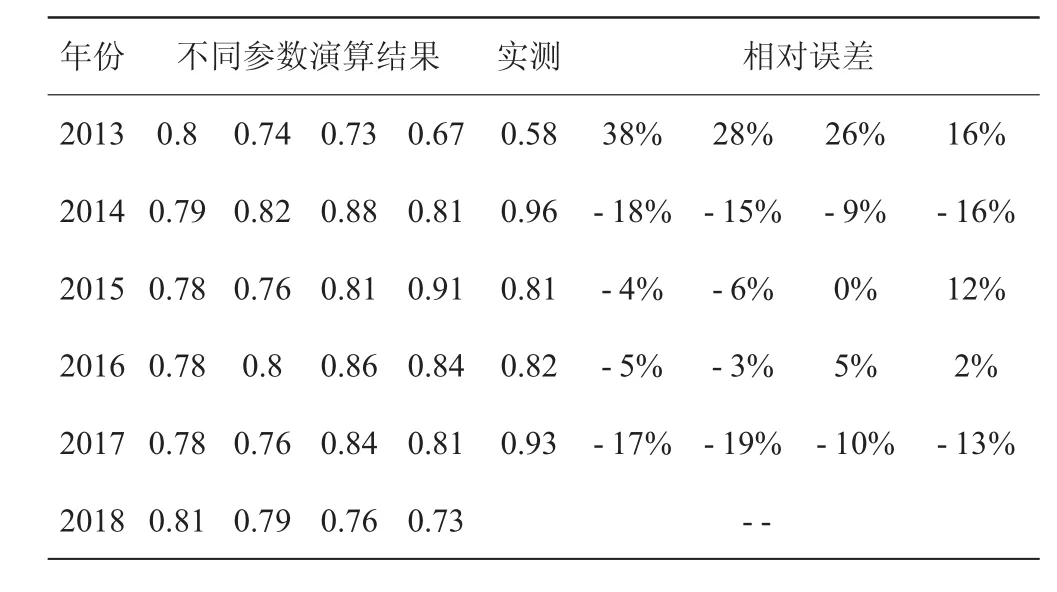
表1 不同参数演算结果及误差 单位:亿m3
4 预报结果分析及径流年内分配
4.1 演算分析
根据《水文情报预报规范》要求,“内陆及干旱地区水量预报的许可误差,取实测值的20%,枯季月径流预报的许可误差,取实测值的30%”、“甲等:合格率≥85%;乙等:85%>合格率≥70%”,判定周期均值迭加法合格率80%,属乙等预报方案;参数选择(1,1,4)情况下ARIMA模型合格率100%,但整体预报结果趋势与实际来水趋势不吻合,参数选择(1,1,3)时,除枯水年不合格外,其他年份误差较小,并且趋势与实际情况较为吻合,故选择参数为(1,1,3)的 ARIMA 模型,此时合格率 80%,也属乙等预报方案。
周期均值迭加法2018年年径流预报结果为0.85亿m3,ARIMA模型预报结果为0.76亿m3。
两种方法均存在极端枯水年预报误差过大问题,应根据预报当年的前期降水量判断是否为极端枯水年,若为极端枯水年应当引入枯水修正系数。
4.2 枯水修正
在完成周期均值迭加预报和ARIMA模型预报的基础上,绘制1985年~2017年径流量与1月~6月降水散点图,分析发现峡门河存在两种明显的枯水现象:①1月~6月降水量80mm~95mm时,年径流量在0.6亿m3左右,称枯水现象A;②1月~6月降水量120mm~130mm时,年径流量在0.7亿m3左右,称枯水现象B,见图3。
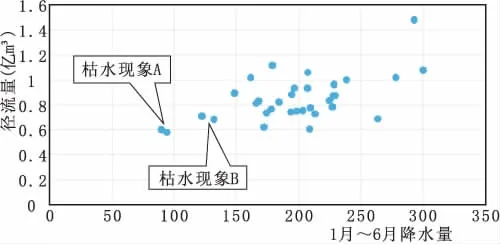
图3 降雨径流散点图
普遍地,当降水量符合枯水现象A时,对周期均值迭加预报结果乘以枯水修正系数kA1,kA1结合2013年预报误差取0.74,对ARIMA模型预报结果乘以枯水修正系数kA2,kA2结合2013年预报误差取0.79。同样,当降水量符合枯水现象B时,对周期均值迭加预报结果乘以枯水修正系数kB1,kB1参照枯水现象A和比例关系取0.89,对ARIMA模型预报结果乘以枯水修正系数kB2,kB2参照枯水现象A和比例关系取0.95,详见表2。

表2 枯水修正系数取值
哈溪站2018年1月~6月自记雨量计实测降水量为85.8 mm,符合枯水现象A,判定2018年为极端枯水年,因此由周期均值迭加法预测2018年峡门河来水量为0.6290亿m3,ARIMA模型预测结果为0.6004亿m3。
4.3 重现期确定
根据33年来水资料序列绘制峡门河年径流频率曲线,确定2018年来水重现期,如图4。
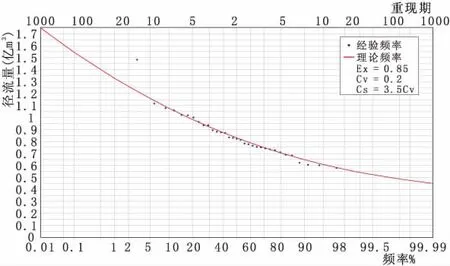
图4 峡门河年径流频率曲线图
枯水适线采用“就低”原则,周期均值迭加预报来水量0.6290亿m3代表频率92.3%,重现期为13年;ARIMA模型预报来水量0.6004亿m3代表频率95.7%,重现期为23年。两种预报结果在实测序列中分别排第5位,第2位,属极端枯水年,预报结果与石羊河流域整体丰枯趋势一致。
4.4 径流年内分配
根据前期降雨径流和枯水修正选择枯水现象A中的代表年2001年作为年内分配的模板,等比例分配,如图5。
由径流年内分配可知,5月~10月径流量占全年78%以上,下半年径流量占全年71%以上,来水高度集中。
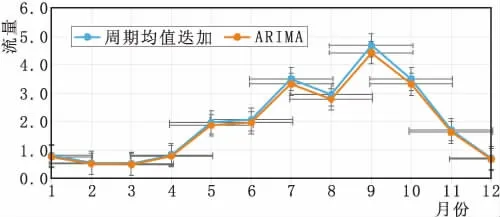
图5 预测2018径流年内分配
5 结论与建议
5.1 结论
1)邻近值对周期均值迭加预报结果影响较大,序列均值对ARIMA模型预报结果影响较大。
2)直接使用预报软件,两种方法都有80%的合格率,能较好地契合峡门河实际水情,但都不能满足枯水年预报精度要求。丰枯程度不同,需要引入不同的枯水修正系数进行枯水修正。
3)除枯水年,两种方法的预报精度也存在差异。偏丰水年周期均值迭加法预报精度明显高于ARIMA模型,平水年ARIMA模型预报精度高于周期均值迭加,但均在10%以内。
4)周期均值迭加需要判定周期是否显著,如果数据序列较短,无法判定周期或显著周期不存在,则周期均值迭加不能使用,同时不同丰枯情况两种预报方法预报精度不同,因此在预报中应当采用尽可能多的资料相互印证。
5.2 建议
经前期降水、预报分析,2018年属极端枯水年,预测峡门河来水量较多年均值偏少二到三成,可能对经济发展产生不利影响,建议相关部门参考预报结果,根据雨水情变化、下游黄羊水库蓄水情况、农田土壤墒情和沿线哈溪镇与黄羊镇城乡供水情况,加强旱情监测,储备抗旱物资,必要时开展人工降雨作业,最大程度降低旱情影响,同时注意防范可能出现的短时强降水。
