基于多引导滤波的图像增强算法∗
2018-12-14刘杰1张建勋1代煜1
刘杰1)† 张建勋1)2) 代煜1)2)
1)(南开大学计算机与控制工程学院,天津 300071)
2)(南开大学机器人与信息自动化研究所,天津 300071)
(2018年7月25日收到;2018年10月11日收到修改稿)
1 引 言
图像增强技术旨在加强图像中的有用信息,同时抑制噪声,以此改善图像质量.依据算法运行时所在空间的不同,一般可分为频域法和空域法两类.频域法[1,2]主要通过一定的规则修正图像的变换系数,之后进行逆变换以实现图像增强,可以较好地避免过平滑梯度信息.空域法则通过分析局部像素对中心像素的影响,进而对中心像素进行调整,其噪声消除效果通常较好,缺点是会过平滑物体边界,代表算法有基于生物视觉特性的Retinex算法[3]和直方图均衡化[4,5]等.
基于引导滤波的图像增强方法主要工作在空间域中,属于空域法的范畴.早期的各向异性扩散算法[6]利用输入图像自身来实现扩散,以避免边界的过平滑.之后的联合双边滤波器(cross bilateral f i lter,CBF)[7]扩展了传统双边滤波算法[8,9]的通用性,引导滤波算法(guided f i lter,GF)[10]则强化了引导图像的重要性.域变换滤波器(domain transform f i lter,DTF)[11]将图像上的曲线进行高维映射,对输入信号进行域变换.梯度域引导滤波算法(gradient domain guided f i lter,GDGF)[12]和加权引导滤波算法[13]分别在滤波中加入一阶边缘感知约束和边界感知权重,使得滤波输出尽量避免光晕效应.递归滤波器(rolling guided f i lter,RGF)[14]将滤波过程扩展到尺度空间,以迭代的形式处理不同尺度的噪声信息.全连接引导滤波[15]引进了一个树相似性作为额外的空间相似性衡量,改善了图像局部区域的自适应性,将整幅图像隐式地视为中心像素的支持区域.文献[16]提高了多通道引导图像的工作效率,文献[17]中提出了一个端到端的可训练引导滤波算法,为改善图像滤波的自适应性提供了新的方向.
此外,还有一些联合滤波方法[18,19]同时考虑输入图像和引导图像中物体的结构信息,使得滤波过程对噪声更加鲁棒,一定程度上提升了图像增强的稳定性.值得说明的是,另一类图像增强方法[20,21]是通过优化能量函数来实现的,求解过程中往往包含大量的矩阵运算,因此时间复杂度较高.
针对上述基于滤波的图像增强方法在图像边界区域的过平滑以及对物体前景结构与背景细小纹理信息区分度不足的缺点,本文将引导滤波理论应用于图像增强,着重对图像进行边缘增强并抑制噪声,进而提升信噪比以实现图像增强.算法首先依据图像降噪理论[22]提出了一个以滤波核为变量的通用图像优化模型,以加权最小二乘的形式来描述图像增强.而后对传统联合滤波中的引导图像进行扩展,以不同滤波器的输出作为基输出,通过集成理论对多个基输出进行合成.最后在图像优化模型中加入正则化项,保证不同滤波器的输出图像具备相当程度的一致性,并以边缘保持滤波器与简单平滑滤波器的差值进行物体边界判定,对输出图像内位于同一物体区域的相邻像素进行平滑.实验结果表明,本文算法具备优良的边缘增强和噪声抑制性能.
2 联合滤波相关理论
近年来,图像滤波理论获得了极大的发展,联合滤波是其中的重要成果,典型算法有联合双边滤波[7]和引导滤波算法[10]等.相较于传统图像滤波,联合滤波的基本思想是在引导图像(输入图像本身也可作为引导图像)上构建空间可变滤波核,将引导图像中的梯度信息迁移到输出图像中,以加强滤波输出中的结构信息.由于联合滤波良好的边缘保持平滑特性,已广泛应用于图像处理和计算机视觉领域[23,24].
不同于传统双边滤波[8,9],联合双边滤波[7]在引导图像G上进行权值计算,其在像素i上的滤波输出为
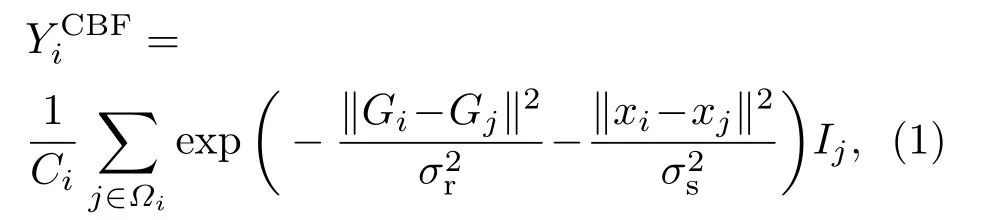
其中Ci为规范化系数,Gi,Gj,xi和xj分别为像素i和j在引导图像G上的灰度值和坐标,和Ij分别为像素i和j在输出图像YCBF和输入图像I上的灰度值,Ωi为以像素i为中心的局部区域,σr和σs用来调整滤波器在灰度空间和空域的强度.当引导图像G上像素i和j的空间关系一定,而灰度相差较大时,滤波算法自适应地调整像素j关于i的权重,即邻像素j位于中心像素i边界外时,其在滤波输出中的影响较低,反之,其在滤波输出中的影响较高.通过这样的处理,输出图像上的边界得到增强,而噪声信息在加权平均求和的过程中被抑制,使得滤波输出的图像质量得到提升.
引导滤波算法[10]以局部线性模型来描述引导图像G与输出图像Y之间的关系,通过与降噪模型的结合构建图像优化目标函数,之后最小化目标函数以实现边缘增强,其在像素i上的滤波输出为
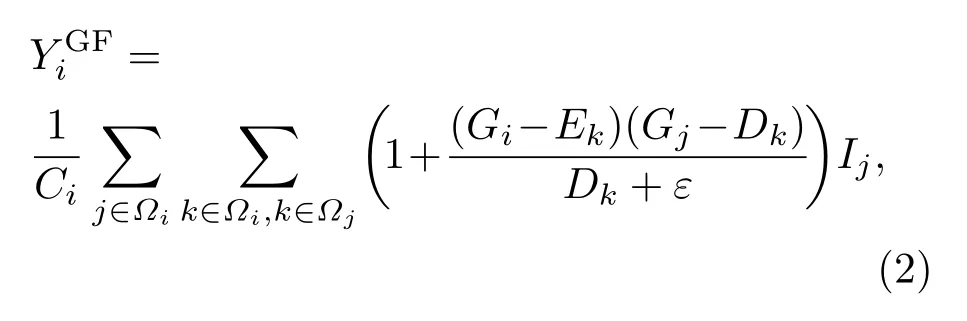
其中Ek和Dk是像素k在引导图像G局部区域内的平均值和方差,ε为正则化项,用以保证局部线性模型的梯度不至于过大,即保持引导图像G与输出图像Y之间的梯度信息具备一致性,该算法关于像素i和j的滤波核为
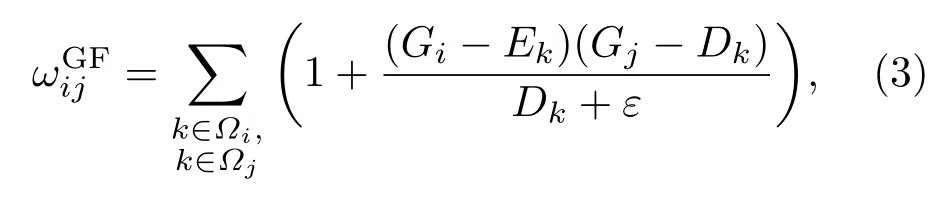
分析可知,当像素i和j的灰度值相差较小,即位于同一物体区域时,方差Dk较小,像素与均值Ek的差异也相对较小,同时由于正则化项ε的值一般远小于方差Dk,因此滤波核的值相对较大,像素j在滤波输出中的支持力度较大.反之,像素j在滤波输出中的支持力度则较小.引导滤波算法更多地考虑了像素在强度空间的相似性,但由于滤波核尺寸与形状的限制以及局部线性模型的局限性,一定程度上影响了滤波输出在图像边界区域的增强效果.
相较于其他图像滤波算法[7,8],引导滤波具备高效性,即其运行时间与滤波核的尺寸无关,这极大地扩展了该算法的应用场景.基于引导滤波模型的以上特点,本文提出了一个基于多引导滤波的图像增强算法,着重改善输出图像中物体边界区域的过平滑现象和光晕效应,以进一步增强结构信息,提升输出图像的质量.
3 算 法
首先提出一个通用图像优化模型,之后以该优化模型为目标函数,将传统引导滤波扩展到多引导滤波,而后加入正则化项确保输出图像内的平滑性和不同滤波输出间的一致性,最终得到高效的滤波输出.
3.1 通用图像优化模型
一般而言,由于图像获取设备和拍摄条件的影响,待滤波图像(输入图像)中总带有较多的噪声,图像滤波的目标是降低这些噪声(小尺度的纹理细节、离群点和光斑等)的影响,突出有用信息(物体的边缘、前景与背景的边界等)以实现图像增强.在引导滤波[10]中,将带噪声的输入信号Ii与输出信号Yi之间的关系描述为

其中ni为输入信号所含的噪声.这些噪声不仅影响了图像中有用信息的表达,更对图像处理的后续步骤造成了很大干扰.
为了提升图像增强的效果,根据已有的图像降噪相关研究[22]和图像优化理论,本节提出了以下图像优化模型:
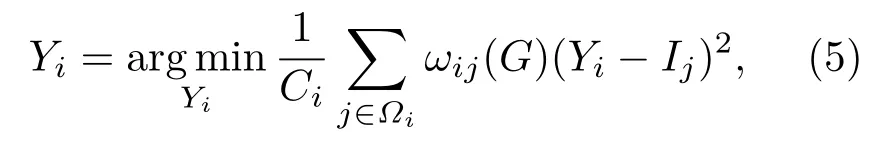
式中滤波核ωij(G)为模型的变量,在引导图像G上进行运算.模型的主要目标为最小化滤波输出Yi与输入信号Ij之间的残差.求解可知,以不同的滤波核为变量,可以生成不同的滤波输出Yi.如第2节中联合双边滤波和引导滤波的输出和,可视为上述图像优化模型以滤波核和ωGF为变量时的解.
目标函数仅仅以滤波核ωij(G)为变量,有利于提高模型的可扩展性,符合常见滤波器的一般形式(加权平均求和),使得已有的图像滤波算法可以方便地应用于该模型.优化模型通过最小化滤波输出Yi和输入信号Ij的残差来保证输出图像Y与输入图像I之间的一致性;并通过不同的滤波核为残差分配相应的权重,来决定邻像素Ij在输出Yi中的支持力度.这样的设置在保证滤波输出一致性(即滤波输出信号必须是改善后的输入信号,而不能是其他信号)的前提下,增强了有用信息的表达,同时降低了噪声对输出信号的干扰,极大地保证了图像增强的效果.
3.2 多引导图像滤波
基于上述目标函数,已有的图像滤波算法可以方便地用于图像优化.分析可知,加权平均求和过程中,引导图像G的质量直接决定了滤波算法的性能表现,尤其在以输入图像为引导图像的情况下,这种情况尤其突出.为了增加滤波算法的鲁棒性,同时更好地利用引导图像中的结构信息,依据集成学习相关理论,本节将基于滤波的图像增强算法扩展为多引导图像滤波.
多引导滤波图像优化模型采用不同的滤波核在引导图像G上进行权重计算,如联合双边滤波核ωCBF、引导滤波核ωGF和梯度域引导滤波核ωGDGF等,便可以得到对应的多个滤波输出Ys(相当于集成理论中的个体学习器),表达为
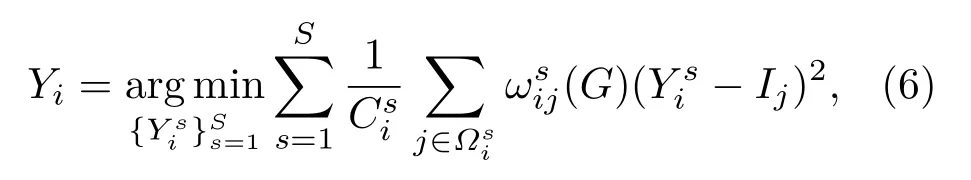
式中用上标s表示不同滤波核ωs对应的滤波输出Ys,S是多引导优化模型中滤波器的最大数目,不同滤波核对应的滤波输出如图1所示,滤波输出Ys满足集成学习理论中对个体学习器准确性(滤波输出图像上结构信息的准确性)和多样性(不同滤波输出间具备一定差异性)的要求.由于传统的图像滤波算法对应的滤波输出已具备较好的图像增强效果,因此为了保持多引导滤波图像优化模型在求解过程中的便利性以及图像滤波的高效性与准确性,本文算法参考传统的联合图像滤波方案[7,10],特定引导图像对应的单一图像滤波核依然采用固定尺寸的矩形窗口.值得一提的是,多引导滤波模型依然继承了上述通用图像优化模型可扩展性强的优点.
分析可知,多引导滤波图像优化模型中基滤波器的数目S与最终滤波输出的质量直接相关.根据集成学习理论,在保持个体学习器多样性和基本准确性的前提下,个体学习器的数目越多,合成学习器的性能通常越好.在已有研究和大量实验的基础上,为了保持所提算法依然可以拥有较好的实时性,采用联合双边滤波[7]、引导滤波[10]、域变换滤波[11]和梯度域引导滤波[12]的滤波输出作为基输出Ys,即将基滤波器的数目S设为4.多引导滤波图像优化模型采用多个滤波核对引导图像进行运算,这同时与集成学习理论中的个体学习器和合成学习器相对应.
已有的一些研究[14]将联合滤波以迭代的形式进行图像处理,文献[18,19]将引导图和输入图或者不同传感器获取的图像作为变量,更多地借鉴了多传感器信息融合的思想,可视为多引导滤波的一类特例.本文算法则更多地采用了集成学习中“合成强化”的思想,利用现有研究成果,将不同滤波器的输出进行合成,使得多引导滤波模型有着清晰的物理意义,这种较强的可解释性为算法的稳定性提供了坚实的理论基础.

图1 不同滤波算法的输出图像 从左到右依次为:输入图像,联合双边滤波输出,引导滤波输出,递归滤波输出Fig.1 .Filtering outputs of dif f erent image f i lters.From left to right:input image,result of CBF,result of GF,result of RGF.
3.3 滤波输出的平滑性与一致性
依据集成学习相关理论,在得到多个个体学习器(即滤波输出Ys)之后,便需要一个有效的集成策略将它们结合起来以得到最终的结果.文献[25]中指出,图像滤波后的输出应与输入图像保持相当程度的一致性,同时保证图像的结构信息保持不变.对上述理论进行合理的拓展可知,不同滤波器对应的输出图像Ys之间也应该保持一致性,本文称之为滤波输出间的一致性.多引导滤波的输出图像由(6)式中不同滤波器的输出Ys合成,由于Ys之间存在差异性,因此出现离群点的可能较大.在自然图像中,位于同一物体区域的像素一般符合局部平滑性假设,因此所提算法以局部平滑性来消除离群值,进一步提升多引导滤波输出¯Y的增强效果,本文称之为输出图像内的平滑性.将上述滤波输出间的一致性和图像内的平滑性加入目标函数,表达式为

式中λ0用来控制整个正则化项的强度,λ1用以控制局部平滑性的强度,分别用来表达滤波输出间的一致性和图像内的平滑性.由于基输出已具备一定的图像增强效果,通过上述处理,进一步保证了不同滤波输出Ys间具备相关性,从而使得合成滤波输出可以更为稳定和准确.
由以上分析可知,只有当像素不处于边界区域时,才符合局部平滑性假设,因此需要判定像素i是否与像素i−1位于同一物体区域,即像素i−1是否处于i所在的物体边界外.因此,λ0为一个常数,而λ1是关于像素i的一个变量,同时为了减少多引导模型的计算复杂度,算法用之前得到的滤波输出Ys来检测边界情况,λ1的计算公式为
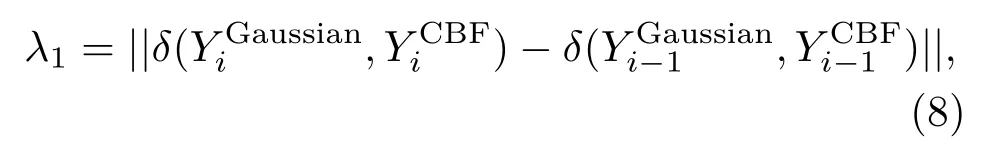
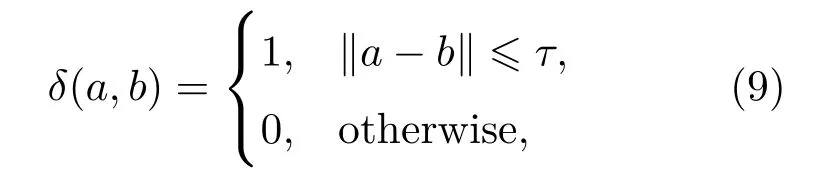
其中τ为阈值,即当相邻的两个像素在灰度空间相差较小时,两个像素属于同一个物体区域,指导函数的值为1,反之,则为0.为基于空间相似性的高斯滤波,表达式为
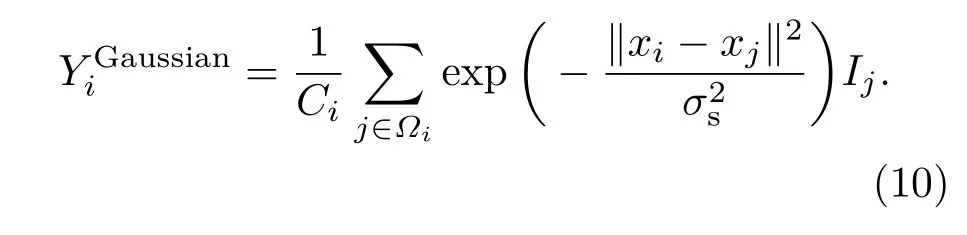

图2 边缘检测可视化 从左到右依次为:输入图像,高斯滤波与联合双边滤波输出图像间的差异图,二值化差异图Fig.2 .Visualization of boundary regions.From left to right:input image,dif f erence of Gaussian f i ltering output and CBF output,binary image.
分析可知,当像素i位于边界区域时,双边滤波由于额外考虑了像素在色度空间的相似性,因此边界外像素joutside对滤波输出Yi的支持力度较小;而高斯滤波仅考虑空间相关性,因此无论边界内像素jinside还是边界外像素joutside对滤波输出的支持力度都相对较大.在参数相同的情况下,位于边界区域的像素i对应的相对较大.即当小于阈值τ时,像素i位于平坦区域,将该像素在边界图(如图2中的二值化差异图所示)中的值置为1,反之,置为0.具体到(7)式,即像素i与i−1在边界图中的值不相等时,则不处于同一个物体区域,不进行图像内的局部平滑,反之,则进行平滑.因此通过设置合适的阈值τ,便可得到像素i是否与邻像素i−1位于同一物体区域,边界区域的检测情况如图2所示,图中物体的结构信息清晰准确,因此上述算法可以有效地用于边缘检测.
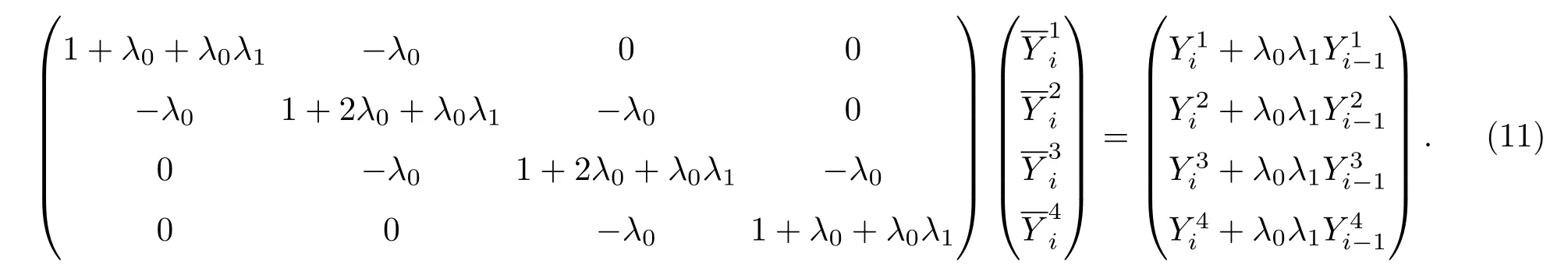
对以上公式分析可知,在图像优化模型中加入图像内的局部平滑性约束和滤波输出间的一致性约束,在具体实现上相当于对不同滤波输出的加权平均,这与集成学习理论中个体学习器的合成策略相对应,在理论上保证了多引导滤波算法的图像增强效果.为了更好地展示多引导滤波模型对信号的增强效果,给出其在一维信号上的输出,如图3所示,可以看出,在一维信号发生较大变化的地方,边界保持能力优于其他先进的滤波器,同时保持了对平缓区域细小噪声的抑制.
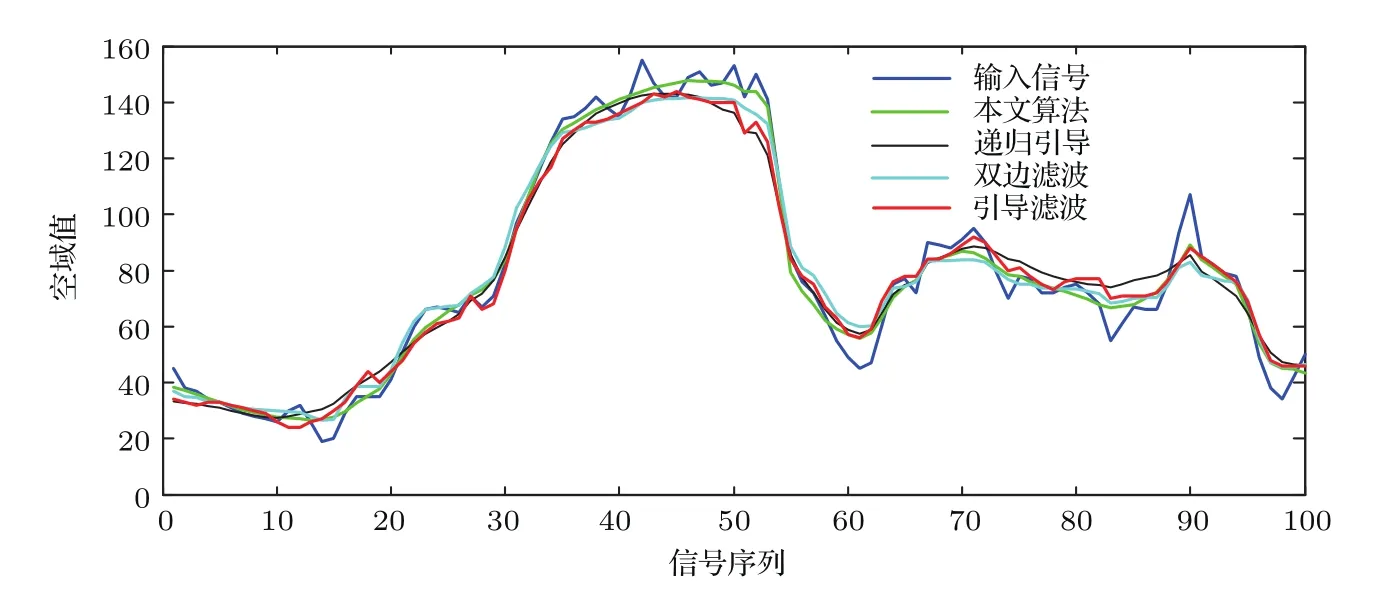
图3 本文算法在一维信号上的滤波输出Fig.3 .Filtering outputs of proposed method on 1D signals.
综上所述,基于多引导滤波的图像增强算法流程图如图4所示.
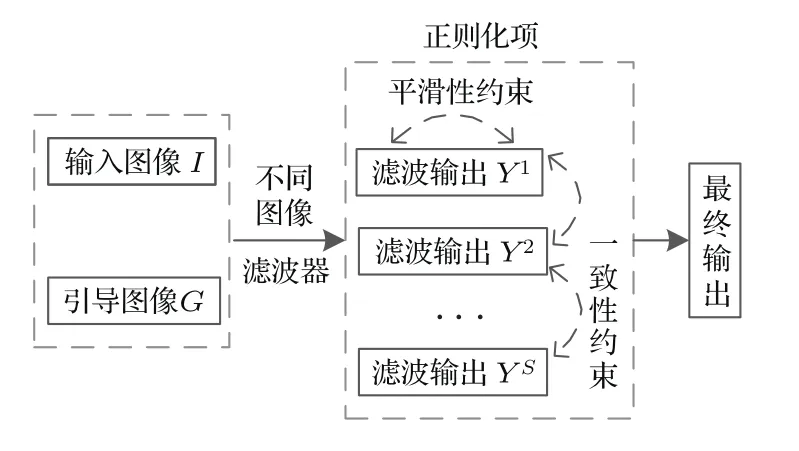
图4 本文算法流程图Fig.4 .The f l ow diagram of proposed algorithm.
3.4 算法实时性分析
已有的研究表明,本文采用的基滤波算法[10,11,12,26]均具备O(n)的线性时间复杂度(双边滤波器在具体实施中采用快速算法[26]),n为图像上像素的总数目.而所提算法主要的计算消耗为不同滤波器在引导图上的权值计算(即基输出Ys的计算),因此其时间复杂度为O(Sn).由于滤波核的数量S为常数,因此所提算法依然具备线性时间复杂度.
与具备线性时间复杂度的图像滤波算法(如引导滤波算法[10])相比,所提算法时间花费较大.在现今先进图像滤波器时间花费为毫秒级的背景下,所提算法的时间花费依然可以满足大部分的应用场景需求.与基于优化理论的图像增强算法[20,21]以及不具备线性时间复杂度的滤波算法[7]相比,所提算法则具备相当程度的实时性优势.
4 实验与分析
为了更好地展示(7)式中所提算法的性能表现,本节采用灰度平均梯度(gray mean grads,GMG)和峰值信噪比(peak signal to noise ratio,PSNR)作为客观评价指标进行评价,两指标的定义分别为
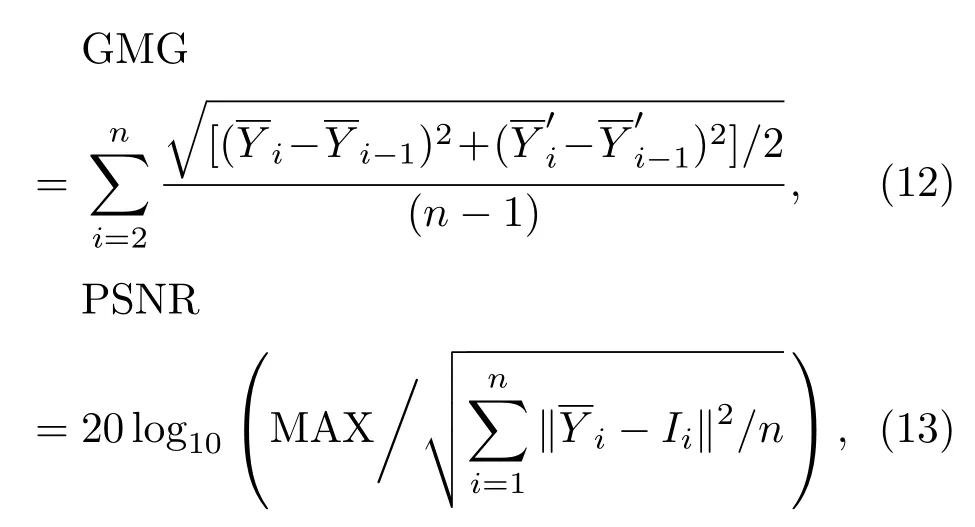
算法的参数设置情况和运行环境为:正则化项参数λ0设置为0.25,平滑性参数λ1依据像素i与i−1是否位于同一个物体区域相应设置为0和1,在数字图像上运行多引导滤波算法时阈值τ为26,所有图像滤波器的局部滤波区域Ω为9×9的矩形,联合双边滤波器中σr=0.1,σs=3,引导滤波器中的正则化项ε=0.04.所有算法均在2.7 GHz双核Intel Core i5处理器,8 G内存的条件下,基于Matlab 2016a编程实现.
4.1 噪声消除
噪声抑制是图像增强中的必经步骤,通过有效地抑制噪声在图像中的分布,可以更好地突出物体结构信息,进而扩大图像中不同特征信息之间的差别,最终提升图像质量.边界区域作为图像中主要的有用信息,使得图像滤波算法可以通过边缘保持实现噪声消除,所提算法及对比算法的滤波输出如图5所示.

图5 不同滤波算法的降噪效果展示 从左到右依次为:输入图像,GF算法滤波输出,WLS算法滤波输出,所提算法滤波输出Fig.5 .Noise reduction results of dif f erent f i ltering method.From left to right:input image,result of GF,result of WLS,result of ours.
由图5可知,在输入图像中,噪声分布较多,非均匀性很严重,前景(图中的数字)部分分布着与背景类似的强干扰,图中数字边界部分的噪声甚至影响了图像中显著性物体的表达.图片经过所提算法滤波后,对前景与背景区域分布的噪声进行了有效抑制,降噪后输出图像精确地保持了物体的边缘信息,如图中数字的边界部分清晰锐利,同时可以很好地处理平滑区域中小尺度的纹理信息.与引导滤波算法和WLS算法的滤波输出相比,所提算法得到的滤波输出画面更为清晰,且显著性物体的结构也保持得更为准确.同时,这也表明所提算法采用的多引导滤波思想,具备提升滤波算法鲁棒性和准确性的作用.在不影响图像有用信息表达和不改变图像结构的前提下,所提算法使得滤波输出具备更好的视觉效果.
图5更多地从主观视觉效果方面展示了本文算法的性能,为了更加精确地展示算法降噪的效果,表1采用权威的SIPI图像数据库[27]来测试所提算法的性能,以GMG和PSNR两个指标对滤波输出进行衡量.
结果表明,本文算法起到了较好的边缘保持平滑作用,滤波输出的图像增强效果提升较为明显.经过多引导滤波处理后,图像的GMG降低了32%,相较于先进的GF算法,也有15%左右的降幅,与全局优化算法WLS效果相近.在PSNR指标上,滤波输出后的信噪比相较于其他算法得到了2.5%—7.5%的明显提升,充分说明了所提算法在图像降噪方面的优良性能,部分图像的滤波输出如图6所示,图中显著性物体的边缘区域均得到了准确的保持,如人像的头发边缘以及飞机与雪山的交界部分,这反映出所提算法优良的边缘保持特性.与此同时,图像中背景区域分布的噪声得到了强有力的抑制,如头像背后的窗户与湖面上方的天空等,这表明算法在采用多引导滤波后,对前景与背景区域有较强的辨别能力以及优良的降噪性能.
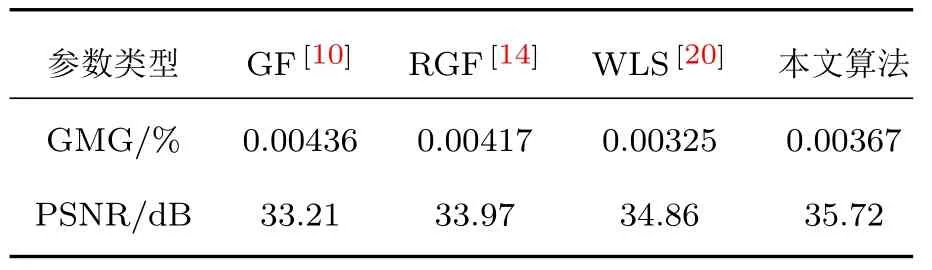
表1 不同算法的GMG和PSNR比较Table 1 . Comparison of image quality of dif f erent methods by GMG and PSNR.
4.2 信息增强
信息增强主要指的是对图像细节信息部分的扩充,在本文中,滤波输出作为基本层,输入图像和基本层之间的差异称之为信息层,加权后的信息层与基层的和为图像增强结果.根据信息增强的定义可知,当基本层中结构信息不具备较高精确性时,噪声可能被作为结构信息随之放大,导致图像增强结果破坏图像中的有用信息.好的图像信息增强结果不仅可以准确保持图像轮廓,而且可以合理地丰富图像的细节信息,因此利用信息增强实验可以有效地对多引导图像滤波算法进行边缘保持性能的测试.所提算法及对比算法的信息增强结果如图7所示.

图6 SIPI图像数据库部分图像滤波输出展示 第一行,SIPI数据库中输入图像;第二行,所提算法滤波后输出图像Fig.6 .Filtering outputs of some images on SIPI Image Database.First row,input images of SIPI database;second row,fi ltering outputs of ours.

图7 不同滤波算法在数字图像上的信息增强展示 从左到右依次为:输入图像,GF算法增强结果,RGF算法增强结果,WLS算法增强结果,所提算法增强结果Fig.7 .Detail enhancement results of dif f erent methods on some digital images.From left to right:input image,result of GF,result of RGF,result of WLS,result of ours.
由图7可知,所提算法的信息增强效果在丰富图像细节的同时,主观视觉上更加自然和真实,通过对基输出的有效集成,使得多引导滤波模型在滤波过程中具备更加准确的边缘保持特性.GF和RGF算法受限于引导图像中有限的结构信息以及没有针对性地平滑性处理,使得物体边缘的增强效果出现了不正常的过曝,如金色球体和花朵边缘的泛白.由于所提算法综合利用了不同滤波器的输出,因此对图像中前景部分的判定更为精准,进而对图像中主要结构信息的检测更为准确和稳定,这直接反映到了增强图像的视觉效果上.同时,在物体色彩的展现上,与其他算法相比,本文算法也更加准确,如叶子的颜色在所提算法的增强图中更为真实.由于对信息层一定比例的放大,用信息增强实验来测试所提算法,相较于图6中的滤波输出图像,增强图像可以更为有效地展示滤波算法的边缘保持效果.为了分析算法在信息增强中各层的表达能力,图8在单一图像行(视为一维信号)上对输入层、基本层、信息层和增强结果进行了展示.
由图8可以发现,多引导滤波算法所得到的基本层对输入信号拟合得极为准确,在信号突变部分依然保留了清晰锐利的边界,验证了所提算法通过多引导滤波方式,对多个基输出进行集成的有效性.因此,增强结果不仅合理丰富了输入信号的细节,而且保持了原信号的结构信息,使得输入信号的主体内容在最大程度上得以保留,从而清晰地反映出多引导滤波算法对显著性结构信息判定的准确性.在图像变化平缓的区域(与数字图像中的细小纹理区域相对应),增强后信息的变化则相对较大,在增强图像上表现为细节的丰富性,这反映出多引导滤波算法对前景与背景信息的辨别能力,为得到高质量的图像增强效果提供了强有力的保证.在输入信号发生较剧烈变化(边界区域)时,信息层在相应位置也并没有出现不合理的梯度变化,实验结果证明本文算法具备较好的信息增强效果.
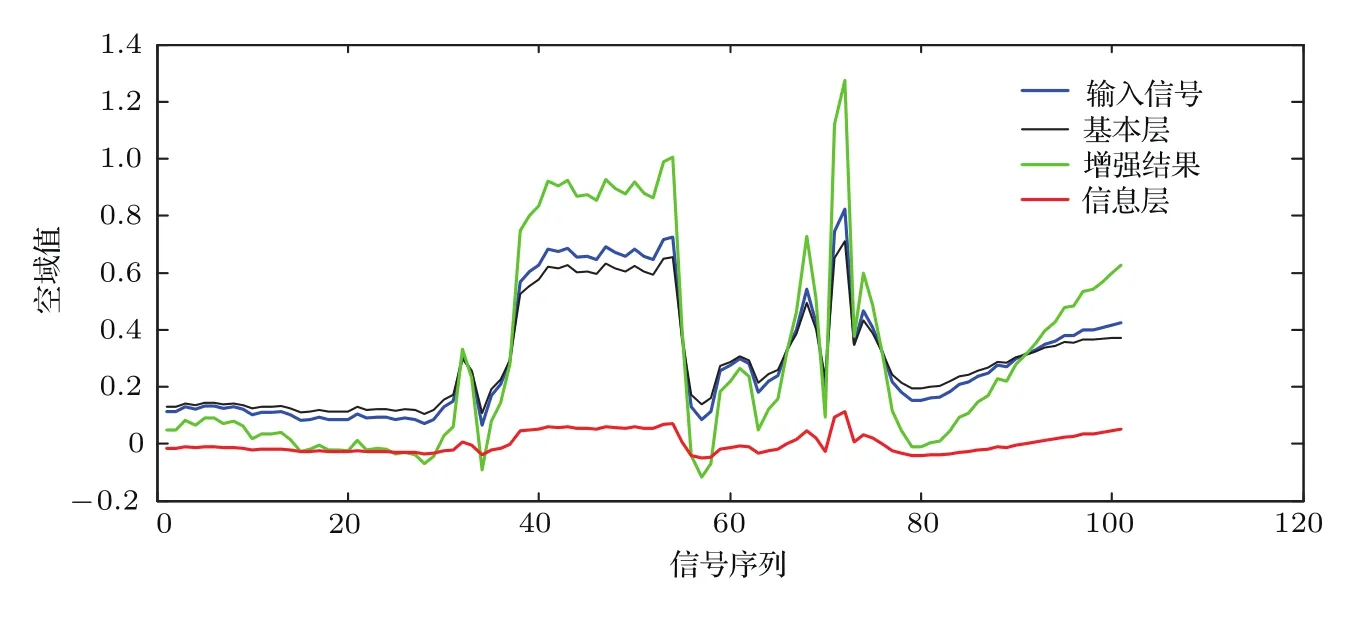
图8 多引导滤波算法在一维信号上的信息增强展示Fig.8 .Detail enhancement results of proposed method on 1D signals.
5 结 论
本文提出了一个基于多引导滤波的图像增强算法.首先对基于滤波的图像增强技术进行归纳分析,得到一个以滤波核为变量的通用图像优化模型.而后将联合滤波中的引导图像进行扩展,并在优化模型中加入正则化项以保证滤波输出间的一致性.扩展后的多引导滤波模型更好地利用了引导图像中的结构信息,使得多引导滤波的输出图像中边缘信息更加准确和稳定,细小的噪声信息也得到了充分的抑制.通过针对性的噪声消除和信息增强实验,表明本文算法具备良好的图像增强效果,相较于已有的图像滤波增强技术,本文算法处理后的图像信噪比有着较大提升,这为后续的图像处理提供了良好的基础.
